Megjegyzés (bináris Hamming kód)
Új interpretációt adunk a
bináris Hamming kódhoz. Lássuk példaként a 16 db hétbetűs kódszóból álló kódot!
Ez szolgáltatta az 5.9 "hazudós barkochba" feladat megoldását
is és ott a III. konstrukcióban a
egyenletrendszer állította elő. Az ismeretlenek indexei itt 1, 2, ..., 7; ezek helyett "beszédesebb", ha az indexszel a változó együtthatóira utalunk:
Tehát a változókat xijk jelöli, ahol az i, j, k bitek nem mindegyike 0 és ahol xijk együtthatója az egyes egyenletekben rendre i, j, k. Az első egyenletben azok a változók szerepelnek 1-es együtthatóval, amelyek indexének első jegye 1-es, a második egyenletben azok, amelyek második jegye 1-es, végül a harmadikban azoknak a változóknak 1 az együtthatója, amelyek indexében az utolsó bit 1-es. Az ábrán a változókat Venn-diagrammba rendeztük, a Hamming kódba a változók olyan értékrendszere tartozik, amelynél a három halmaz közül bármelyikben szereplő négy változó értékének összege zérus (mod 2).
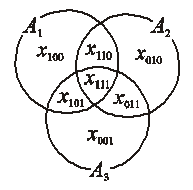
Ehhez hasonlóan adhatjuk meg
az általános esetben is a bináris Hamming kódot. Annál a kódnál, amelyben a
szavak hossza, az egyenletek száma és a kódszavak száma rendre
5.11
(Juhász Istvántól és Szegedy Balázstól is hallottam)
Egy kém az ellenséges ország televíziójánál dolgozik. Esténként alkalma van az adásba
kerülő 8×8-as fekete fehér tábla egyetlen mezőjének színét
megváltoztatni. Nem feltétlenül szükséges változtatnia. Sajnos sohasem tudja
előre, hogy milyen mintázatú lesz a 64 mező, amikor eléje kerül. Hányféle
információt tud így küldeni a TV-n keresztül?
I. megoldás
Tekintsünk egy lehetséges információt! Legyen pld u1 az az információ,
üzenet, hogy "támadás várható északról". Az üzenet vevőjénél és az
azt közvetítő kémnél kell lennie egy a dekódolást illetve a kódolást segítő
iratnak, amelyben föl van sorolva, hogy az u1 üzenetet mely
sakktáblaszínezések jelentik. Bonyolult lenne mindig lerajzolni a sakktáblát.
Ehelyett rakjuk inkább sorba a 64 mezőt, és minden sakktáblaszínezésnek
feleltessünk meg egy-egy 64 hosszúságú 0-1 sorozatot, pld 0 jelentheti a fehér
színt, 1 a feketét. Ha a sorozat 11. eleme 1-es, akkor a megfeleltetett
színezésben a sakktábla 11. mezője fekete. Az u1 üzenetet
ezek után a 64 hosszúságú 0-1 sorozatok egy U1 részhalmaza
továbbítja. Megpróbáljuk meghatározni egy megfelelő U1
részhalmaz tulajdonságait.
Az u1
üzenetet el kell tudnia küldeni a kémnek, bármilyen minta is kerül elé. Ez azt
jelenti, hogy bármely 64 hosszúságú 0-1 sorozathoz található U1-ben
azzal teljesen megegyező vagy tőle csak egy helyen eltérő sorozat. Másképpen:
1) az U1 elemei köré írt 1 sugarú Hamming gömbök lefedik az
összes 64 hosszúságú 0-1 sorozatot.
Tudjuk, hogy
bármely 1 sugarú Hamming gömbben éppen 1 + 64 = 65 elem (0-1 sorozat) van,
összesen pedig 264 darab 0-1 sorozat van. Ennek alapján, ha az U1-ben
szereplő 0-1 sorozatok száma n1, akkor n1 ˇ
(64 + 1) ≥ 264. Ebből (mivel 65 nem
osztja 264-t) n1 > 264/65. Ez
bármely információra igaz, és az összes információhoz tartozó összes színezések
legfeljebb 264-en vannak, így ha összesen k-féle információt
küldhetünk, akkor
Megmutatjuk, hogy 64 információ átküldése lehetséges. 64 helyet próbálkozhatunk 1, 2, 4, 8
mezővel, ezekben az esetekben a kém által elküldhető információk száma 1, 2, 4,
8, és viszonylag könnyű is megtalálni a színezések, illetve a 0-1 sorozatok
megfelelő Ui részhalmazait. Az általánosítás azonban nehezen észrevehető.
Ennek oka az, hogy túl sok szabadságunk van, valójában a fenti esetekben mindig
elég eggyel kevesebb mező is ugyanannyi üzenet átküldésére. Ennek esélyét
beláthatjuk, ha az előző bekezdésben leírtakat 64 mező helyett 63-mal is
végiggondoljuk. Valóban, ilyenkor a Hamming gömb elemeinek száma 64, 264/64
most egész, így lehetséges, hogy ni = 264/64
legyen, tehát az adódó kˇ 263/64 ≤
n1 + n2 + ... + nk
≤ 263 egyenlőtlenség nem zárja ki, hogy az üzenetek
k száma 64 legyen.
63 mezőn csak
akkor küldhetünk át 64 üzenetet, ha bármelyik üzenethez tartozó Ui
halmaz egyes elemei köré írt Hamming gömbök egymáshoz diszjunktak (nincs közös
elemük) és lefedik az összes 63 hosszú 0-1 sorozatot. Ez éppen azt jelenti,
hogy mindegyik Ui halmaz egy-egy tökéletes 1-hiba javító kód.
Legyen az u1
információhoz tartozó U1 halmaz a 6 egyenlettel meghatározott
26 - 1 hosszú szavakból álló Hamming kód. Legyen továbbá x
tetszőleges 63 hosszú 0-1 sorozat. A sorozatokat a következőkben vektorokként
kezeljük, koordinátánként mod 2 adjuk őket össze. Toljuk el U1-et
x-szel. Ezen a következőt értjük: tekintsük U1 összes
elemét (vektorát) és mindegyikhez külön-külön adjuk hozzá az x
vektort. Az így kapott vektorok halmazát U1 + x
-szel jelöljük. Képezzük ezt a halmazt minden lehetséges x-re.
Így 263 halmazt kapunk. Állítjuk, hogy
1') bármely x-re, az U1 + x elemei
köré írt 1 sugarú Hamming gömbök lefedik az összes 63 hosszúságú 0-1 sorozatot.
2) bármelyik kettő halmaz vagy megegyezik egymással vagy diszjunkt.
Ha állításaink igazak, akkor készen vagyunk, az egymástól diszjunkt eltoltak
lesznek az üzeneteknek megfelelő Ui halmazok.
Belátjuk a fenti 1'), 2) állításokat. Az U1 halmaz elemei köré írt 1 sugarú
Hamming gömbök uniója az összes 63 hosszúságú 0-1 sorozat (vektor) halmaza,
hiszen U1 tökéletes kód. Az U1 + x
elemei köré írt 1 sugarú Hamming gömböket úgy is képezhetjük, hogy az U1
elemei körüli gömböket toljuk el x-szel. Ezért az U1
+ x elemei köré írt 1 sugarú Hamming gömbök uniója U1
elemei körüli gömbök uniójának, azaz az összes sorozatnak (vektornak) az
eltoltja. Ha az összes sorozatot (vektort) eltoljuk ugyanazzal a sorozattal
(vektorral), akkor az összes sorozatot (vektort) megkapjuk, így az 1') állítás
igaz.
Ha az U1
+ x, U1 + y halmazok nem
diszjunktak, akkor van közös elemük, tehát valamely a, b
U1-beli vektorokkal a + x = b
+ y. Ebben az esetben az U1 + x
halmaz tetszőleges a' + x elemére (a'
az U1-ben van) és az U1 + y
halmaz bármely b' + y elemére (b'
az U1-ben van)
Mivel U1 lineáris kód, így (a' - a + b) és (b' - b + a) az U1 elemei, tehát a' + x az U1 + y, b' + y pedig az U1 + x halmazban van, azaz a két halmaz valóban megegyezik egymással. A 2) állítást is bebizonyítottuk.
II. megoldás
(csak konstrukció, Pósa Lajos)
Konstrukciót adunk 64 információra. Az egyik mezőt kidobhatjuk. A maradék mezőkre írjuk rá
1-tól 63-ig a számokat kettes számrendszerben 6 biten (000001-111111)! Ha adott
a tábla színezése, akkor adjuk össze a fekete mezők számait bitenként mod 2.
Így egy X számot kapunk. A fogadó fél is így fogja majd dekódolni
az üzenetet. Legyen az információ, amit át akarunk adni Y
(szintén 6 biten tárolva). Képezzük az X - Y
bitenkénti differenciát! Ha ez 000000, akkor nem kell változtatnunk, egyébként
változtassuk meg a neki megfelelő mező színét.
Megjegyzések
I. Ha átgondoljuk a bináris Hamming kódnak
a szakkör elején ismertetett interpretációját, akkor észrevehetjük, hogy a II.
megoldásban adott konstrukció az I. megoldás konstrukciójának frappáns
átfogalmazása, amellett, hogy konkrét kódolási-dekódolási algoritmust is ad.
II. A II. megoldásból az is kiderül, hogy 64
mezővel akkor is megoldható 64 információ továbbítása, ha kapott mintán a
kémnek mindenképpen kell változtatnia. A 64. mező száma lehet 000000, és ha a
63 mezőre vonatkozó módszer esetén nem kellene változtatni, akkor a 000000 mező
színét módosítja a kém.
"Ideális 1001-es"
(emlékeztető: lásd az "ideális 101-es" feladatot és
megoldását a 19. szakkör anyagában!)
Ebben a feladatban a
természetes számok bizonyos részhalmazait keressük. A számokat mindig kettes
számrendszerben leírva képzeljük, illetve alább így is említjük őket. Két számot
nem a szokásos módon adunk össze, hanem kettes számrendszerbeli alakjuk
megfelelő jegyeit modulo 2, és átvitel nélkül adjuk össze (pld 1100110 + 10011
= 1110101).
A természetes számok
(pontosabban azok kettes számrendszerbeli alakjainak) egy I1001
részhalmazát "ideális 1001-es"-nek nevezzük,
1. ha h I1001-ben van, akkor h0 is I1001-ben van; (h0
a h dupláját, tehát azt a számot jelöli, amelyet úgy kapunk, hogy h
mögé írunk egy 0-t)
2. ha h és j is I1001-ban van, akkor h +
j is ott van.
3. ha 1001 is I1001-ben van (itt 1001 az
egy-nulla-nulla-egy számot, azaz a kilencet és nem az ezeregyet jelenti).
Hány "ideális
1001-es" részhalmaza van a természetes számok halmazának?
Megoldás
Az "ideális 101-es" feladat "Segítség"
részében leírt megfeleltetésből indulunk ki, természetes számok helyett F2 feletti (azaz az együtthatók és a műveletek
mod 2 értendők) polinomokról beszélünk. Az ottani megoldásból kiderül, hogy 1.
és 2. azzal ekvivalens, hogy az "ideális 1001-es" halmaz valamely p
polinomból és p összes többszöröséből (azaz polinom-szorosából) áll. A
3. tulajdonság pedig pontosan akkor teljesül, ha p az x3
+ 1 polinom osztója, azaz x3 + 1 előáll p-nek egy (F2
feletti) polinommal vett szorzataként. Tehát az "ideális 1001-es
halmazok" leszámlálása ekvivalens az x3 + 1 polinom
osztóinak leszámlálásával. F2 felett, azaz mod 2 számolva is
teljesül az x3 + 1 = (x + 1) ˇ (x2
+ x + 1) azonosság, és itt már egyik tényezőt sem lehet tovább bontani
kisebb fokú polinomok szorzatára, a két tényező már felbonthatatlan, idegen
szóval irreducibilis. Az F2 test feletti polinomok körében
is igaz a számelmélet alaptétele (ezt a szakkör őszi félévében igazoltuk, de a
szakköri anyagban egyelőre nincs részletesen leírva). Ennek következményeként x3
+ 1 összes osztója, tehát az összes lehetséges p polinom x3
+ 1 irreducibilis osztóiból állítható össze. A két irreducibilis osztóból
összesen négy osztó állítható össze: p1 = 1, p2
= x + 1, p3 = x2 + x + 1 és p4
= (x + 1) ˇ (x2 + x + 1) = x3
+ 1. Tehát négy "ideális 1001-es halmaz" van. A p1-nek
megfelelő halmaz az összes természetes számból áll, a p2
által meghatározott pedig azokból a természetes számokból, amelyeknek kettes
számrendszerbeli alakjában páros darab 1-es van. A p3 és p4
által generált "ideális 1001-es halmazokat" bonyolultabb leírni,
szükség van hozzá, hogy a természetes számok kettes számrendszerbeli alakjának
jegyeit három csoportba osszuk. Alább aláhúzással, dőlt szedéssel, illetve
normál szedéssel jelöltük a csoportokat egy példaként vett szám kettes
számrendszerbeli alakján:
tehát minden harmadik jegy tartozik ugyanabba a csoportba. A p3 által generált "ideális 1001-es halmaz" azokból a kettes számrendszerbeli alakokból áll, amelyeknél ha felírjuk a három csoportba tartozó 1-esek számát, akkor három ugyanolyan paritású számot kapunk. A p4 által generált halmaz pedig azokból a kettes számrendszerbeli alakokból áll, amelyek mindhárom csoportban páros darab 1-est tartalmaznak.
Hétszögminták
Ebben a feladatban egy
szabályos hétszög csúcsaira írunk 0-t vagy 1-et. Összesen 27=128
ilyen kitöltés van. A kitöltések egy I7 részhalmaza "7-szögre
ideális",
1. ha h az I7-ben van, akkor h bármely (n·360°/7-kal
való) elforgatottja is I7-ben van.
2. ha bármely két I7-beli kitöltés csúcsonként és mod 2 számított összege
is I7-ben van.
A kitöltéseknek hány "7-szögre ideális" részhalmaza van?
Megoldás
A feladat megoldható az esetek alapos elemzésével, de a tapasztalat azt mutatja, hogy a
diákok gyakran elnézik a két legizgalmasabb "7-szögre ideális"
részhalmazt. Alább egy, az absztrakt algebrába hajló megoldást ismertetünk.
Visszavezetjük
a feladatot az "ideális 101-es",
"ideális 1001-es" problémákkal analóg kérdésre. Tekintsük az F2
test feletti polinomok F2[x] halmazát. Minden polinomhoz
hozzárendeljük a hétszög egy "kitöltését" a következő módon. A
hétszög csúcsait számozzuk meg az egyik forgásirányban a 0., 1., 2., ..., 6.
sorszámokkal, és a p polinom tagjait írjuk fel sorban, körkörösen a
hétszög csúcsaira. A polinom konstans tagja kerüljön a 0., az elsőfokú tag az
1. csúcshoz és így tovább, a hetedfokú tag értelem szerint megint a 0. csúcshoz
kerül. A hétszögnek a p polinomhoz rendelt kitöltésének értéke egy
adott csúcson legyen egyenlő a p polinomnak az ahhoz a csúcshoz írt
tagjai együtthatóinak összegével. A p polinomhoz így rendelt kitöltést &phi(p)
fogja jelölni. Tehát φ(p)-ben az i. csúcshoz írt
érték a p polinom azon tagjai együtthatóinak összegével egyenlő, amely
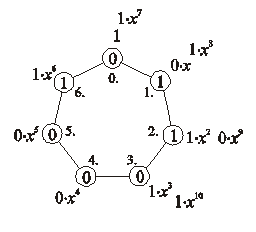
tagok kitevője 7-tel osztva i maradékot ad. Például a p(x)
= 1 + 0·x + 1·x2 +
1··3 + 0·x4 +
0·x5 + 1·x6 +
1·x7 + 1·x8 +
0·x9 + 1·x10
polinomhoz rendelt kitöltésnél a 0. csúcshoz írt szám a 0, mert az 1 + 1·x7
polinom együtthatóinak összege 0. Ehhez hasonlóan az 1.
csúcshoz írt szám 1, mert 0·x+1·x8
együtthatóinak összege 1. φ(p)-ben 2., 3., 4., 5., 6. csúcsokhoz
írt számok rendre 1, 0, 0, 0, 1.
1.' ha h I10000001-ben van, akkor x·h0 is I10000001-ben van;
2.' ha h és j is I10000001-ban van, akkor h + j is ott van.
3.' az x7 + 1 polinom I10000001-ben van.
Valóban, 1'. az 1., 2'. a 2. tulajdonság közvetlen következménye, 3'. pedig abból adódik, hogy nem üres "7-szögre ideális" halmazban a 2. tulajdonság miatt (azt két egymással megegyező polinomra alkalmazva) benne van az azonosan 0 kitöltés, és az x7 + 1 polinomhoz rendelt φ(x7 + 1) kitöltés is azonosan 0. Nevezzük az 1'., 2'., 3'. tulajdonsággal rendelkező polinom-halmazokat "ideális 10000001-es"-nek. Állítjuk, hogy
A) "ideális 10000001-es" halmaz képe a φ leképezésnél "7-szögre ideális";
B) egymástól különböző "ideális 10000001-es" halmazok képe különbözik egymástól.
Valóban, az 1'), 2') tulajdonságból következnek az 1), 2) tulajdonságok, így az A) állítás igaz. B) igazolásához 3'.-re is szükség van. Ha valamely p, q polinomokra φ(p) = φ(q), akkor p - q előáll a x7 + 1, x8 + x, x9 + x2, ... polinomok összegeként, azaz p - q = r(x)·(x7 + 1), ahol r(x) is polinom. Az 1'., 2'., 3'. tulajdonságokból következik, hogy r(x)·(x7 + 1) minden "ideális 10000001-es" halmazban benne van, így 2'. szerint q pontosan akkor van benne egy "ideális 10000001-es" halmazban, ha abban p = q + r(x)·(x7 + 1) is benne van. Ezzel megmutattuk, hogy ha két "ideális 10000001-es" halmaz képe megegyezik egymással, akkor a két "ideális 10000001-es" halmaz is megegyezik egymással.
Mindezekből következik, hogy az üres halmaztól különböző "hétszögre ideális" kitöltés-halmazok kölcsönösen egyértelmű megfeleltetésben állnak az "ideális 10000001-es" halmazokkal. Ez utóbbiak az "ideális 101-es" feladat megoldásának mintájára az x7 + 1 polinom irreducibilis felbontásának segítségével határozhatók meg. A felbontás:
Ebből következik, hogy 9 db "7-szögre ideális" kitöltéshalmaz van, az üres halmazon kívül az alábbi nyolc:
| generáló polinom | leírás | elemszám | |
| 1. | p1 = 1 | az összes kitöltés | 27 |
| 2. | p2 = x + 1 | az 1-esek száma páros | 26 |
| 3. | p3 = x3 + x2 + 1 | az ábrán látható 8, és ugyanezek a 0 és 1 felcserélésével. | 24 |
| 4. | p4 = x3 + x + 1 | 3. tükörképe | 24 |
| 5. | p5 = (x + 1)·(x3 + x2 + 1) | 2. és 3. közös része | 23 |
| 6. | p6 = (x + 1)·(x3 + x + 1) | 2. és 4. közös része | 23 |
| 7. | p7 = x6 + x5 + x4 + x3 + x2 + x + 1 | azonosan 0, és azonosan 1. | 21 |
| 8. | p8 = x7 + 1 | azonosan 0 | 20 |

Megjegyzés (polinom-kódok)
A táblázatban
található 3. (és 4.) "hétszögre ideális" halmaz régi ismerős:
bináris, lineáris, 1-hiba javító, tökéletes kód. "Hétszögre ideális"
halmaz definíciója szerint bináris és lineáris. Ez a halmaz azért 1-hiba javító
kód, mert lineáris
kód, és az azonosan 0
kitöltésen kívül mindegyik kitöltésben legalább három darab 1-es van. Tökéletessége
egyszerű leszámlálásból adódik.
Ezt a kódot
tehát a következőképpen is értelmezhetjük. Tekintsük a 0, 1 jelekből képezhető
hétbetűs szavak halmazát. Minden szónak feleltessünk meg egy F2
feletti legfeljebb hatod-fokú polinomot. Egy szó pontosan akkor kódszó, ha a
neki megfeleltetett polinom osztható a p3 = x3 + x2 + 1 polinommal. p3-at
legfeljebb harmad-fokú polinommal szorozva kapunk legfeljebb hatod-fokú
polinomot. Összesen 24 darab legfeljebb harmad-fokú polinom van F2
felett, így p3-nak összesen 24 legfeljebb
hatod-fokú többszöröse van. Ezek a kódszavak.
Az így értelmezett polinom-kód előnye, hogy nem kell megjegyeznünk a kódszavakat, csak a p3
polinomot kell fejben tartanunk. Minden legfeljebb harmadfokú polinomhoz (azaz
lényegében minden négy hosszú 0-1 sorozathoz) rendelünk egy információt, és a
kívánt információt úgy küldjük el, hogy a neki megfelelő polinomot megszorozzuk
p3-mal, és az így kapott polinom együtthatóit továbbítjuk. A
fogadó fél egyszerű polinom-osztással fejtheti vissza az üzenetet: a kapott
0-1 sorozatot legfeljebb hatod-fokú polinomként értelmezi és p3-mal
osztja. Ha nem történt hiba, akkor nem lesz maradék és a hányados együtthatói
alkotják az információt. Ha 1 hiba történt akkor az elküldeni kívánt polinom
helyett az attól az 1, x, x2, x3, x4,
x5, x6 polinomok valamelyikével eltérő
polinomot dekódoltuk. Ebben az esetben lesz maradék, méghozzá éppen annyi
amennyi az 1, x, x2, x3, x4,
x5, x6 polinomok közül megfelelőnek a p3-mal
való osztási maradéka. Állítjuk, hogy
A) az 1, x, x2,
x3, x4, x5, x6
polinomok nem oszthatók p3-mal;
B) az 1, x, x2,
x3, x4, x5, x6
polinomok különböző maradékot adnak p3-mal osztva.
A) azt jelenti, hogy észrevehetjük, hogy 1 hiba történt, B) pedig azt, hogy ki is tudjuk javítani. A)
igaz, hiszen p3 osztja az x7 + 1 polinomot,
így az attól 1-gyel eltérő x7 polinomhoz, és annak minden
osztójához (tehát az 1, x, ..., x7 polinomokhoz )
relatív prím. B) azért igaz, mert ha xm és xn
(m < n) azonos maradékot ad p3-mal osztva,
akkor
xm - xn = xm + xn
= xm · (1 + xn-m) osztható p3-mal,
azaz q = (xn-m + 1) osztható p3-mal
(n-m<7). Ebben az esetben a
polinom is osztható p3-mal, ami azért nem lehetséges, mert p3 harmadfokú, és q és q* közül az egyik legfeljebb harmadfokú, de különbözik p3-tól.
Ha tehát előre felírjuk az 1, x, x2, x3, x4, x5, x6 polinomok p3-mal való osztási maradékait, akkor az üzenet dekódolásakor, a polinom-osztás során nyert maradék alapján azonnal rájöhetünk, hogy hol volt a hiba.
Házi feladat:
4.10
Ha adott egy négyzet alakú Hi
számtáblázat, akkor elkészíthetjük a kétszer akkora oldalhosszúságú
Ennek a kódnak az alkalmazásával küldte a fényképeket a Mariner 10 szonda a Földre. A 64 sorozat 64 színnek felelt meg, egy sorozat egy képpont (pixel) színét határozta meg. Az alábbi képet a szonda visszafelé fotózta, rajta együtt látható a Föld és a Hold.

Ajánlott olvasmányok:
Freud Róbert: Lineáris algebra, ELTE Eötvös Kiadó, Budapest, 1998.
A 10. fejezetben sok kódelméleti feladatot olvashatunk, és a Hamming kódokon túl a BCH kódokkal is megismerkedhetünk. A gimnazisták többségének azonban a könyv nagy részét el kell olvasni az utolsó fejezet megértéséhez. Érdemes.
Hraskó András és Szőnyi Tamás: Hibajavító kódok, az Új matematikai mozaik című kötetben, Typotex kiadó, Budapest, 2002.
A cikkben a Hamming kódok dekódolásának leírása és a Golay kódok leírása jelent lényegesen új információt.