A TI-83 grafikus zsebszámológép programozása
(Egy kis emlékeztető:
- a programmódba a PRGM billentyű leütésével kerülhetünk;
- az utasításokat a PRGM billentyű leütése után a CTRL, I/O és EXEC menüből
választhatjuk;
- használható a CATALOG billentyű is az utasítások beszúrására;
- a matematikai függvényeket általában a MATH billentyűvel érhetjük el;
- a TEST billentyű alatt találjuk a relációs jeleket és logikai függvényeket;
- a STO → billentyűvel
adhatunk értéket az egyes változóknak.)
1. feladat:
Határozzuk meg az ax
2 + bx + c = 0 másodfokú
egyenlet gyökeit!
A programot érdemes megírni, hiszen elég gyakran használjuk
a megoldóképletet, s nem mindig "szépek" az együtthatók és a gyökök.
A program algoritmusa:
Bekérjük a, b, c-t (a ≠ 0);
Kiszámoljuk a diszkriminánst;
D előjelétől függően kiírjuk a gyökök számát és a gyököket.
Megoldás:
Legyen a program neve MF.
Egy lehetséges kódolás:
PROGRAM:MF
: Prompt A,B,C
: B2 – 4AC → D
: If D < 0
: Then
: Disp "NINCS VALOS GYOK"
: Stop
: End
: If D = 0
: Then
: Disp "EGY GYOK VAN"
: Disp -B/2/A
: Else
: Disp "KET GYOK VAN"
: Disp (-B+√D)/2/A
: Disp (-B-√D)/2/A
: End
Megjegyzések:
1. Célszerű volt a D segédváltozót bevezetnünk, hiszen
többször hivatkoztunk rá.
2. A STOP utasítás megállítja a program futását, így a D
= 0 feltételt csak akkor vizsgáljuk, ha a program nem állt meg,
vagyis ha D < 0 nem teljesült.
3. A legegyszerűbb megoldás - ti.
: B2 – 4AC → D
: Prompt A,B,C
: Disp (-B+√D)/2/A
: Disp (-B-√D)/2/A
- szintén tökéletes. Ekkor azonban a felhasználónak tudnia kell, hogy ha a gép
hibát jelez, akkor nincsenek valós gyökök; illetve a kiírásnál észre kell
vennie, ha a két gyök megegyezik.
4. Természetesen az algoritmus könnyen átírható, ha az
esetleges komplex gyököket is ki szeretnénk íratni. (Sőt ha a gépünk komplex
módban van, akkor ez automatikusan teljesül.)
2. feladat:
Ismerjük egy háromszög három oldalát. Döntsük el, hogy
hegyesszögű, derékszögű vagy tompaszögű!
A három oldalból határozzuk meg a háromszög lehetőleg minél
több adatát!
Megoldás:
Legegyszerűbb a Pitagorasz-tétel, illetve a koszinusz-tétel
módosítását alkalmazni.
Az egyik lehetőség az összetett feltétel vizsgálata: ha az
a2 + b2 > c2, b2 + c2
> a2, a2 + c2 > b2
feltételek teljesülnek, a háromszög hegyesszögű; ha az egyik egyenlőtlenség
helyett egyenlőség van, a háromszög derékszögű; ha pedig az egyik relációs jel
fordított, a háromszög tompaszögű.
Elég bonyolult a teljes vizsgálat programozása.
Egyszerűbben járhatunk el, ha tudjuk, hogy a legnagyobb
oldal pl. c. Ilyenkor elég a legnagyobb oldalra felírni az összefüggést: a
hegyesszögű, derékszögű és tompaszögű háromszögekre rendre a2 + b2
> c2, a2 + b2 = c2, a2
+ b2 < c2 teljesül.
Ekkor viszont az a, b, c oldalak közül meg
kell határoznunk a legnagyobbat. Ezt ugyan megtehetjük részprogrammal is, de
sokkal egyszerûbb a max függvény használata. (Mivel az argumentumba csak
két számot írhatunk, a max függvényt kétszer használjuk.)
További ügyeskedés: a legnagyobb oldalt
hozzáadva az a2 + b2 > c2
stb. egyenlõtlenségekhez, az így kapott a2 + b2
+ c2 > 2c2 stb.
egyenlõtlenségekben a bal oldal már konstans. A jobb oldalon elég a
maximális oldal értékét ismernünk; nem kell konkrétan tudnunk, hogy
melyik ez a változó.
Ha pedig ismerjük a legnagyobb oldal
értékét, felírhatjuk a háromszög-egyenlõtlenséget az a + b + c >
2max alakban. (Ennek segítségével zárhatjuk ki azokat az a, b, c
számhármasokat, amelyek nem határoznak meg háromszögeket.)
Legyen a program neve HSZ.
Egy lehetséges kódolás:
PROGRAM:HSZ
: Prompt A,B,C
: max(max(A,B),C) →M
: If A + B + C ≤ 2M
: Then
: Disp "NINCS HAROMSZOG"
: Stop
: End
: A2 + B2 + C2 → S
: If S > 2M2
: Then
: Disp "HEGYESSZOGU"
: Else
: If S = 2M2
: Then
: Disp "DEREKSZOGU"
: Else
: Disp "TOMPASZOGU"
: End
: End
Megjegyzések:
1. Mivel az If után csak egy utasítás van, a program második
fele rövidebben is kódolható:
: If S > 2M2
: Disp "HEGYESSZOGU"
: If S = 2M2
: Disp "DEREKSZOGU"
: If S < 2M2
: Disp "TOMPASZOGU"
2. A többi adat meghatározása pl. az alábbiak szerint
történhet:
- terület a Heron-képlet segítségével;
- szögek a koszinusz-tétellel;
- nevezetes körök sugarai a területképletekkel;
- végül a nevezetes szakaszok hossza a rájuk vonatkozó
képletek segítségével.
3. feladat:
Határozzuk meg azokat a négyzetszámokat, amelyek 184-re
végződnek!
Megoldás:
Nyilván elég a legfeljebb háromjegyű természetes számok
négyzetét vizsgálni, mert a magasabb helyiértékek nem befolyásolják az utolsó
három számjegyet. Ugyanakkor ha egy megfelelő háromjegyű számot találunk, az a
magasabb helyiértékeken tetszőlegesen folytatható, s ezért végtelen sok
megoldást kapunk.
Legyen az utolsó három számjegy a, b, c. Mivel (100a + 10b
+ c)2 = 104a2 + 102b2 +
c2 + 2·103ab + 2·102ac + 2·10bc,
innen két tag nem befolyásolja az utolsó három
számjegyet, s ezért a
102b2 + c2
+ 2·102ac + 2·10bc
= x·103+ 184
diofantikus egyenletet kell megoldanunk. Ez még akkor is szerteágazó és
bonyolult, ha figyelembe vesszük, hogy c = 2 vagy c = 8 lehet csak az utolsó
számjegy.
Egyszerűbb egy programot írni, amely végigfut a legfeljebb
háromjegyű számok négyzetén, s megvizsgálja az utolsó három jegyet.
(Tetszőleges s természetes szám utolsó három számjegye 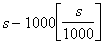 , ahol []
egészrészt jelöl.) A programban M a szám 1000-rel vett maradékát jelenti.
, ahol []
egészrészt jelöl.) A programban M a szám 1000-rel vett maradékát jelenti.
Legyen a program neve N184.
Egy lehetséges kódolás:
PROGRAM:N184
: For(I, 1, 999)
: int(I2/1000) →H
: I2 - 1000H → M
: If M = 184
: Disp I
: End
A futtatás eredménye: 72, 428, 572, 928.
Megjegyzések:
A program gyorsítható, ha kihasználjuk, hogy az utolsó
számjegy csak 2 vagy 8 lehet, s két ciklust alkalmazunk.
4. feladat:
Határozzuk meg annak a valószínűségét, hogy 35 ember
születésnapja az év 35 különböző napjára esik (366 nappal számoljunk).
Megoldás:
Az első ember az év valamelyik napját „elfoglalja”. Annak
valószínűsége, hogy a második ember ettől különböző napon születik,
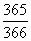
. Együtt már két lehetséges
napot „foglalnak el”, ezért annak valószínűsége, hogy a harmadik ember az első
kettőtől szintén eltérő napon születik,
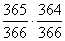
.
Hasonlóan folytathatjuk: N ember esetén a keresett valószínűség
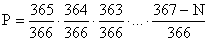
.
A feladatban N = 35 értékkel egy igen hosszú szorzatot
kellene kiszámolnunk. A manuális billentyűzés helyett célszerűnek látszik a
programírás.
Legyen a program neve SZULNAP.
Egy lehetséges kódolás:
PROGRAM:SZULNAP
: 2 →N: 365/366 →P
: While P > 0
: Disp ”N = ”, N
: Disp ”P = ”, P
: Pause
: N + 1 →N
: (367 – N)/366*P → P
: End
(Az elöltesztelős ciklus P > 0 feltétellel fut; cikluson
belül rendre kiírjuk az aktuális N és P értékeket, majd N növelésével
kiszámoljuk P értékét.)
Néhány futási eredmény:
- N = 10-re: P ≈ 88,3%;
- N = 23: P ≈ 49,4%;
- N = 30: P ≈ 29,4%;
- N = 35: P ≈ 18,7%.
Érdekes eredményt kaptunk: ha pl. 23 ember van egy
társaságban, akkor valószínűbb, hogy van közöttük két azonos napon született,
mint az, hogy nincs ilyen pár. (Ezt nevezik születésnap-paradoxonnak.) Egy N =
35 fős osztályban pedig több mint 80% eséllyel mutathat be a tanár egy
„bűvészmutatványt”.
A program P = 0 esetén állna meg. Mivel a kiíratásokkal
együtt elég sokáig tartana a program futása, az On billentyűvel bármikor
megszakíthatjuk a futását.
5. feladat:
Vannak-e olyan pozitív egész számok, amelyek 1999-re
végződnek és 67-tel oszthatók?
Megoldás:
Az egyik lehetséges út a 104x + 1999 = 67y
diofantikus egyenlet megoldása.
Egy másik szép megoldást a számológépes program futási
eredménye alapján találhatunk. (Egyúttal példát látunk arra is, hogy a
számítógép egy sejtéshez segít minket.)
A programban sorra vesszük a természetes számokat, mögéjük
1999-et "írunk", s megnézzük, hogy az így kapott szám osztható-e
67-tel.
Legyen a program neve O67.
Egy lehetséges kódolás:
PROGRAM:O67
: For(I, 0, 999)
: I*10000 + 1999 → S
: If int(S/67) = S/67
: Then
: Disp S
: Pause
: End
: End
A futás eredménye: 441999, 1111999, 1781999, 2451999, 3121999 stb.
Észrevehetjük, hogy az 1999 "előtti" számok: 44,
111, 178, 245 stb. éppen 67-esével növekednek. Ez az észrevétel a skatulyaelv
alkalmazására, egy egzisztencia-bizonyításra ad alkalmat.
Tekintsük az 11999, 21999, 31999, ... , 671999 számokat, s
tegyük fel, hogy közöttük nincs 67-tel osztható (egyébként készen lennénk).
Ekkor a 67-tel vett lehetséges 1, 2, ... , 66 maradékok közül a
skatulya-elv miatt legalább egy maradék ismétlődik, vagyis két szám ugyanazt a
maradékot adja 67-tel osztva. Legyen ez a két szám x1986 és y1986
alakú (x < y).
A két szám maradéka azonos, tehát különbségük osztható
67-tel. A különbségük (y-x)0000 alakú. Mivel (67, 10000) = 1,
csak
67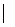 y – x
lehetséges.
Ellentmondásra jutottunk, hiszen x és y az 1, 2, ... , 67 számok
valamelyike.
y – x
lehetséges.
Ellentmondásra jutottunk, hiszen x és y az 1, 2, ... , 67 számok
valamelyike.
Vagyis biztosan található a 11999, 21999, 31999, ... ,
671999 számok között 67-tel osztható.
Megjegyzés:
A feladat általános iskolás korú diákok számára is kitűzhető.
Mielőtt "túlműveltté" válnak diákjaink, az ehhez hasonló feladatokat
egyszerű konstrukciós visszaszorzással oldják meg. Készítsük el az alábbi
táblázatot:
|
|
a
|
b
|
c
|
d
|
e
|
f
|
·
|
6
|
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g
|
h
|
i
|
|
|
|
|
|
|
|
j
|
k
|
l
|
|
|
|
|
|
|
|
m
|
n
|
o
|
|
|
|
+
|
|
|
|
p
|
q
|
r
|
|
|
|
|
|
|
|
|
s
|
t
|
1
|
9
|
9
|
9
|
Közvetlenül adódik i = 9, s innen f = 7. Ekkor az f·67
szorzás elvégezhető: f·67 = 7·67 = 469, g = 4, h = 6.
Mivel h = 6, ezért l = 3, e = 9. 9·67 = 603, j = 6, k = 0.
Az eljárást tovább folytatva végezetül az alábbi táblázatot
kaptuk:
|
|
a
|
b
|
6
|
5
|
9
|
7
|
·
|
6
|
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
|
6
|
9
|
|
|
|
|
|
|
|
6
|
0
|
3
|
|
|
|
|
|
|
|
3
|
3
|
5
|
|
|
|
+
|
|
|
|
4
|
0
|
2
|
|
|
|
|
|
|
|
|
s
|
t
|
1
|
9
|
9
|
9
|
Minden 6597-re végződő szám megoldást ad, a legkisebb
szorzat 441999, mint már korábban láttuk.
6. feladat:
Írjunk programot, mely egy beadott egész számról eldönti,
hogy prímszám vagy összetett szám!
Megoldás:
Az alapalgoritmus egyszerű. A beadott szám négyzetgyökéig
haladva, sorra megvizsgáljuk az egész számokat, hogy találunk-e osztót.
Első közelítésben érdemes csak páratlan számokat vizsgálni,
s csak páratlan osztókat keresni. (Azzal a megfontolással, hogy páros számról
ránézésre megállapíthatjuk, hogy prím vagy nem.)
Legyen a program neve PRIM1.
Egy lehetséges kódolás:
PROGRAM:PRIM1
: Prompt P
: 3 →I
: √(P) →H
: While I ≤ H and int(P/I) ≠ P/I
: I + 2 →I
: End
: If I > H
: Then
: Disp "PRIM"
: Else
: Disp "NEM PRIM, OSZTJA "
: Disp I
: End
Ez az egyszerű algoritmus megvizsgálja a beolvasott páratlan
számot, s ha a vizsgált szám négyzetgyökéig talál egy osztót, akkor azt kiírja;
ha nem talál, akkor a szám prím.
Az algoritmus csak azokra a számokra működik jól, amelyeket
"érdemes" megvizsgálnunk. Nem ad jó eredményt a páros számokra, a P
= 1 értékre és a negatív számokra sem. Ha minden egész számra helyesen működő
programot akarunk írni, akkor le kell kezelnünk ezeket a speciális eseteket.
Pl. a negatív számok kizárása:
A P = ±2 eset:
: If P = 2 or P = -2
: Then
: Disp "PRIM"
: Stop
: End
A páros számok kezelése:
: If int(P/2) = P/2
: Then
: Disp "NEM PRIM,"
: Disp "OSZTJA 2"
: Stop
: End
Végül a P = 1 eset:
: If P = 1
: Then
: Disp "NEM PRIM"
: Stop
: End
Ha a fenti sorrendben beírjuk az utasításokat az eredeti
program
sora után, akkor minden egész számra helyesen működő
prímtesztet kapunk.
Megjegyzés:
Az első három sor helyett alkalmazhatjuk a rövidebb
kódolást is.
7. feladat:
Határozzuk meg az f
0 = 1,
f
1 = (1 – √5)/2
kezdőtagokkal adott f
n+2 = f
n+1 + f
n sorozat
tagjait. Mi lehet a sorozat határértéke?
Megoldás:
Legyen a program neve FIBSOR.
A kódolás:
PROGRAM: FIBSOR
: 1 →A: (1 – √5)/2 →B: 2 →I
: While I < 1000
: A + B →C
: Disp I
: Disp C
: Pause
: B →A: C →B: I + 1 → I
: End
A programban I-vel indexeljük a sorozat elemeit, az A és B
változóban tároljuk a két utolsó tag értékét, s ezek összegéből számítjuk az
aktuális C tagot.
(A programban az első 1000 tagot írathatjuk ki, de
természetesen hamarabb is meg lehet szakítani a program futását.)
A futási eredményeket vizsgálva észrevehetjük, hogy egy
váltakozó előjelű sorozatot kapunk, amelyben a tagok abszolútértéke gyorsan
csökken (pl. a 30. tag 5,33·10-7); s ez alapján az sejthető, hogy a
sorozat 0-hoz tart.
A matematikai vizsgálathoz a homogén lineáris másodrendű
rekurziót kell megoldanunk. Ezt most nem részletezzük, az eredmény fn
= 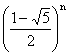 .
.
(Egyébként ha már megsejtettük az explicit alakot, teljes
indukciót is alkalmazhatunk. Segítségével könnyen bizonyítható az állítás, csak
azt kell belátni, hogy 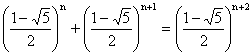 .)
.)
Olyan mértani sorozatot kaptunk, amely kvóciensének 1-nél
kisebb az abszolútértéke; vagyis a sorozat valóban 0-hoz tart.
Előző fejezet
Következő fejezet
Tartalom
![]() , ahol []
egészrészt jelöl.) A programban M a szám 1000-rel vett maradékát jelenti.
, ahol []
egészrészt jelöl.) A programban M a szám 1000-rel vett maradékát jelenti.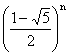 .
.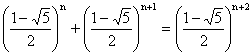 .)
.)