A Casio CFX-9850 grafikus zsebszámológép programozása
A továbbiakban a rövid programozástechnikai emlékeztető után
néhány egyszerű programot s ezekhez kapcsolódó módszertani problémát vizsgálunk
meg. Ezek a programok elsősorban konkrét célfeladatok lesznek;
remélhetőleg ezekben az esetekben célszerűen és eredményesen tudjuk alkalmazni
a zsebszámológépet.
Rövid emlékeztető
(Ez a tömör
összefoglaló nem pótolhatja a gépkönyv tanulmányozását!):
A programmód elérése a főmenüből a PRGM menüponttal
lehetséges. Ezután a programfájlokkal a felkínált műveleteket végezhetjük. A
fontosabbak a következők:
EXE: futtatás;
EDIT: szerkesztés;
NEW: új program létrehozása.
Az új program létrehozásakor meg kell adni annak nevét,
ezután nekiláthatunk a szerkesztéshez. A felkínált menüpontok közül a
fontosabbak:
TOP, BTM: a szerkesztett program elejére, ill. végére
ugorhatunk;
SYBL: ezen szimbólumok között található pl. a szövegkezelő ”
(idézőjel).
A karakterek és sorok szerkesztése a hagyományos módon
történik:
MENU billentyű: főmenübe ugorhatunk;
EXIT: egy szinttel visszaléphetünk;
QUIT: kilépés a programszerkesztőből;
ON: alapállapotba hozás (speciálisan programok megszakítása);
INS, ALPHA: üzemmódok.
Az utasításokat a megfelelő menükből olvashatjuk be (nem
lehet őket pl. karakterenként begépelni; de ezt az is mutatja, hogy az
utasítások kisbetűket is tartalmaznak).
A programszerkezet szigorúan kötött. Az utasításokat egymás
után, sorrendben gépelhetjük be, s három szimbólum választhatja el őket: :,
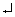 vagy a kiíró utasítás
háromszöge: Δ.
vagy a kiíró utasítás
háromszöge: Δ.
Programok szerkesztésekor a PRGM billentyű kínálja fel a
fontosabb algoritmikus struktúrákat:
COM: elágazás, ciklusok;
CTL: megszakító utasítások;
JUMP: ugró utasítások;
?, Δ: beviteli és kiíró művelet;
: : utasítások elválasztása soron belül;
REL: relációs jelek.
A számítástechnikai változóknak értéket a → billentyűvel
adhatunk; változónév bármely betű lehet.
Feladatok
1. feladat:
Határozzuk meg az Ax
2 + Bx + C = 0 másodfokú
egyenlet gyökeit!
Megoldás:
A programot érdemes megírni, hiszen elég gyakran használjuk
a megoldóképletet, s nem mindig "szépek" az együtthatók és a gyökök.
A program algoritmusa:
bekérjük A, B, C-t (A ≠ 0);
kiszámoljuk a diszkriminánst;
D előjelétől függően kiírjuk a gyökök számát és értékét.
Legyen a program neve MF.
Egy lehetséges kódolás:
Megjegyzések:
1. Célszerű volt a D segédváltozót bevezetnünk, hiszen
többször hivatkoztunk rá.
2. Figyelni kell a műveletek precedenciájára is: a -B/2*A
kódolás nyilván helytelen. (Csak megemlítjük, hogy a -B/2A kódolás helyes, de
ezt jobb, ha nem is jegyezzük meg.)
3. Az adatbevitel barátságosabbá tehető, ha kiírjuk, hogy
melyik változó értékét kívánjuk beolvasni. Pl. alkalmazhatjuk az
”A = ”:? →A
beolvasási technikát.
Az ”A = ”? →A esetén pedig egy sorba kerül az ’A =’
és a ’?’.
4. A legegyszerűbb megoldás - ti.
====== MF ======
? →A: ? →B: ? →C
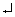
B
2 – 4AC →D
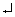
(-B + √D)/2/A Δ
(-B – √D)/2/A Δ
szintén helyes. Ekkor azonban a felhasználónak tudnia kell,
hogy ha a gép hibát jelez, akkor nincsenek valós gyökök; illetve a kiírásnál
észre kell vennie, ha a két gyök megegyezik. (Ugyanígy nem kezeltük le a
programban az A = 0 esetet sem.)
5. Az algoritmus könnyen fejleszthető, ha a komplex gyököket
is ki szeretnénk íratni. (A gép ui. kiírja.)
2. feladat:
Határozzuk meg azokat a természetes számokat, amelyek 13-mal
nagyobbak a számjegyeik szorzatánál.
Megoldás:
Ennek a tipikus célfeladatnak a kétjegyű természetes számok
körében az
ab + 13 = 10a + b
diofantikus egyenlet szolgáltatja a megoldásait. Az egyenlet szorzattá
alakítható:
(a – 1)(10 – b) = 3,
ahonnan könnyű a befejezés: a két tényező csak a 3 társosztói közül kerülhet
ki.
A matematikai háttérhez hasonlóan a program algoritmusa sem
nehéz: egyszerűen végignézzük a kétjegyű számokat, s kiírjuk azokat, amelyekre
a feltétel teljesül.
A kétjegyű számokat egymásba skatulyázott ciklusok
segítségével generáljuk.
Legyen a program neve SZORZ+13.
Egy lehetséges kódolás:
A futási eredmény 27 és 49.
(A 49-et a program kétszer írja ki. Ez a gép
„lelkivilágának” egy bosszantó tulajdonsága miatt van: a gép az utolsó
számított értéket (utasítás hiányában) kiírja a képernyőre. Akit ez zavar,
írjon pl. egy záró ”VEGE” utasítást.)
A kétjegyű számokra most már van megoldásunk. Háromjegyű (és
többjegyű) számokra a felírható diofantikus egyenlet megoldása egyre nehezebbé
válik. Ezzel szemben programozástechnikailag lényegében nem lesz bonyolultabb a
feladat, mindössze több ciklust kell egymásba ágyaznunk.
De itt is felvetődik egy probléma: előre tudnunk kell, hogy
hány jegyű számokat szükséges vizsgálnunk. Márpedig ezt a kérdést pusztán egy
algoritmussal nem tudjuk eldönteni, vagyis már ennek az egyszerű feladatnak a
számológépes megoldása sem nélkülözheti teljesen a matematikai apparátust.
Tekintsük az (n + 1)-jegyű számra felírt 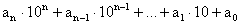 = anan-1…a1a0
+ 13 egyenletet (ahol ai számjegyek,
= anan-1…a1a0
+ 13 egyenletet (ahol ai számjegyek, 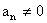 ).
Ha a bal oldalon az első tag kivételével a többit elhagyjuk; a jobb oldalon
pedig an kivételével a többi számjegy helyére 9-est írunk, azt
kapjuk, hogy
).
Ha a bal oldalon az első tag kivételével a többit elhagyjuk; a jobb oldalon
pedig an kivételével a többi számjegy helyére 9-est írunk, azt
kapjuk, hogy 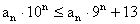 .
.
Ez az egyenlőtlenség csak n < 2 esetén teljesülhet,
vagyis a keresett szám legfeljebb kétjegyű lehet. Ezzel a megjegyzéssel most
már teljes a megoldásunk.
3. feladat:
Határozzuk meg annak a valószínűségét, hogy 35 ember
születésnapja az év 35 különböző napjára esik (366 nappal számoljunk).
Megoldás:
Az első ember az év valamelyik napját „elfoglalja”. Annak
valószínűsége, hogy a második ember ettől különböző napon születik, 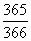 . Együtt már két lehetséges
napot „foglalnak el”, ezért annak valószínűsége, hogy a harmadik ember az első
kettőtől szintén eltérő napon születik,
. Együtt már két lehetséges
napot „foglalnak el”, ezért annak valószínűsége, hogy a harmadik ember az első
kettőtől szintén eltérő napon születik, 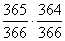 .
Hasonlóan folytathatjuk: N ember esetén a keresett valószínűség
.
Hasonlóan folytathatjuk: N ember esetén a keresett valószínűség 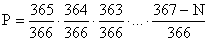 .
.
A feladatban N = 35 értékkel egy igen hosszú szorzatot
kellene kiszámolnunk. A manuális billentyűzés helyett célszerűnek látszik a
programírás.
Legyen a program neve SZULNAP.
Egy lehetséges kódolás:
(Az elöltesztelős ciklus P > 0 feltétellel fut; cikluson
belül rendre kiírjuk az aktuális N és P értékeket, majd N növelésével
kiszámoljuk P értékét.)
Néhány futási eredmény:
- N = 10-re: P ≈ 88,3%;
- N = 23: P ≈ 49,4%;
- N = 30: P ≈ 29,4%;
- N = 35: P ≈ 18,7%.
Érdekes eredményt kaptunk: ha pl. 23 ember van egy
társaságban, akkor valószínűbb, hogy van közöttük két azonos napon született,
mint az, hogy nincs ilyen pár. (Ezt nevezik születésnap-paradoxonnak.) Egy N =
35 fős osztályban pedig több mint 80% eséllyel mutathat be a tanár egy
„bűvészmutatványt”.
A program P = 0 esetén állna meg. Mivel a kiíratásokkal
együtt elég sokáig tartana a program futása, az On billentyűvel bármikor
megszakíthatjuk a futását.
4. feladat:
Írjunk programot, amely egy adott számról eldönti, hogy
prím-e.
Megoldás:
Lényegesen kevesebb „gépeléssel” jár a megoldás, ha csak az
1-nél nagyobb páratlan számokat vizsgáljuk. Ekkor a felhasználónak persze
tudnia kell, hogy milyen számokra nem működik helyesen a program.
Legyen a program neve PRTESZT.
Egy lehetséges kódolás:
Az algoritmus egyszerű: a beadott P szám I páratlan osztóit
keressük √P-ig. A ciklus kétféleképpen
állhat le:
- ha túljutottunk √P-n, ekkor P prím;
- ha nem, akkor I egy osztója P-nek.
Számológéppel támogatott problémamegoldás
Véleményem szerint ez a számológépek alkalmazásának egyik
legfontosabb területe.Arról van szó, hogy a matematikai feladatmegoldás
folyamatában, ennek mintegy részeként alkalmazzuk a kalkulátort. Pl. egy ilyen
tipikus helyzet, amikor adott futási eredményből (sok eset végigpróbálása után)
sejtésünk támad a megoldási módszert illetően. Erre példa a következő feladat.
5. feladat:
Van-e olyan pozitív egész szám, amely 2001-re végződik és
17-tel osztható?
Első megoldás:
Az egyik lehetséges út a 10
4x + 2001 = 17y
diofantikus egyenlet megoldása; ezt most nem részletezzük.
Második megoldás:
A diákok leggyakoribb próbálkozása a maradékok vizsgálatával
történik.
2001 ≡ 12 (mod 17),
10
4 ≡ 4 (mod 17).
Ezután a 2001, 12001, 22001 stb. számok (mod 17) maradékait
vizsgáljuk; ezek rendre 12, 4 + 12, 2·4 + 12, 3·4 + 12, … x·4 + 12 stb. A
maradékok tehát 4-esével nőnek, s mivel véges sok maradék van, előbb-utóbb
(legkésőbb a 18. lépésben) biztosan lesz ismétlődés.
A kapott maradék-sorozat: 12, 16, 3, 7, 11, 15, 2, 6, 10,
14, 1, 5, 9, 13, 0, 4, 8, 12, s innen már ismétlődik. Egy 17-hosszú ciklust
kaptunk. Ami a feladat szempontjából érdekes, az x = 14 értékre 142001 osztható
lesz 17-tel.
Harmadik megoldás:
Írjunk egy programot a feladatra!
A programban sorra vesszük a természetes számokat, mögéjük
2001-et "írunk", s megnézzük, hogy az így kapott szám osztható-e
17-tel.
Legyen a program neve OSZT17.
A futás eredménye: 14, 31, 48, 65, 82, 99 stb, vagyis ezen
számok „mögé” 2001-et írva 17-tel osztható számokat kapunk. (A program futását
természetesen most is megszakíthatjuk.)
Negyedik megoldás:
Szép megoldásra lelhetünk a futási eredmény vizsgálata
alapján. Észrevehetjük, hogy a 2001 "előtti" számok: 14,
31, 48, 65 stb. éppen 17-esével növekednek. Ha pl. 142001 és 312001 osztható
17-tel, akkor a különbségük (170000) is osztható lesz.
Ez az észrevétel a skatulyaelv alkalmazására, egy
egzisztencia-bizonyításra ad alkalmat.
Tekintsük a 2001, 12001, 22001, ... , 162001 számokat, s
tegyük fel, hogy közöttük nincs 17-tel osztható. Ekkor a 17-tel vett lehetséges
1, 2, ... , 16 maradékok közül a skatulya-elv miatt legalább egy maradék
ismétlődik, vagyis két szám ugyanazt a maradékot adja 17-tel osztva. Legyen ez
a két szám 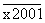 és
és 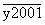 alakú (x <
y, x lehet 0 is). A két szám maradéka azonos, tehát különbségük osztható
17-tel. A különbségük
alakú (x <
y, x lehet 0 is). A két szám maradéka azonos, tehát különbségük osztható
17-tel. A különbségük 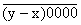 alakú. Mivel
(17,10000) = 1, csak 17
alakú. Mivel
(17,10000) = 1, csak 17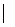 y – x lehetséges.
Ellentmondásra jutottunk, hiszen x és y a 0, 1, 2, ... , 16
számok valamelyike. Vagyis biztosan található a 2001, 12001, 22001, ... ,
162001 számok között 17-tel osztható.
y – x lehetséges.
Ellentmondásra jutottunk, hiszen x és y a 0, 1, 2, ... , 16
számok valamelyike. Vagyis biztosan található a 2001, 12001, 22001, ... ,
162001 számok között 17-tel osztható.
Ötödik megoldás:
A feladat általános iskolás korú diákok számára is
kitűzhető. Mielőtt "túlműveltté" válnak diákjaink, az ehhez hasonló
feladatokat egyszerű konstrukciós visszaszorzással oldják meg. (Érdekes, hogy
az előző, pusztán egzisztencia okoskodás mellett ez tisztán konstrukciós
megoldás lesz.)
Készítsük el az alábbi táblázatot:
|
|
a
|
b
|
c
|
d
|
e
|
f
|
·
|
1
|
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g
|
h
|
i
|
|
|
|
|
|
|
|
j
|
k
|
l
|
|
|
|
|
|
|
|
m
|
n
|
o
|
|
|
|
+
|
|
|
|
p
|
q
|
r
|
|
|
|
|
|
|
|
|
s
|
t
|
2
|
0
|
0
|
1
|
Közvetlenül adódik i = 1, s innen f = 3. Ekkor az f·17
szorzás elvégezhető: f·17 = 3·17
= 51, g = 0, h = 5.
Mivel h = 5, ezért l = 5, e = 5. 5< · 17 = 85, j = 0, k = 8.
Az eljárást tovább folytatva végezetül az alábbi táblázatot
kaptuk (vigyázni kell az átvitelekre):
|
|
|
|
8
|
3
|
5
|
3
|
·
|
1
|
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5
|
1
|
|
|
|
|
|
|
|
|
8
|
5
|
|
|
|
|
|
|
|
|
5
|
1
|
|
|
|
+
|
|
|
|
1
|
3
|
6
|
|
|
|
|
|
|
|
|
1
|
4
|
2
|
0
|
0
|
1
|
Tehát minden 8353-ra végződő szám megoldást ad; a
legkisebb szorzat 142001, mint már korábban láttuk.
6. feladat:
Határozzuk meg az f
0 = 1, f
1 = (1 –√5)/2
kezdőtagokkal adott f
n+2 = f
n+1
+ f
n sorozat tagjait. Mi lehet a sorozat határértéke?
Megoldás:
Legyen a program neve FIBSOR.
A kódolás:
A programban I-vel indexeljük a sorozat elemeit, az A és B
változóban tároljuk a két utolsó tag értékét, s ezek összegéből számítjuk az
aktuális C tagot. (A programban az első 1000 tagot írathatjuk ki, de
természetesen hamarabb is meg lehet szakítani a program futását.)
A futási eredményeket vizsgálva észrevehetjük, hogy egy
váltakozó előjelű sorozatot kapunk, amelyben a tagok abszolútértéke gyorsan
csökken (pl. a 30. tag 5,42·10-7); s ez alapján az sejthető, hogy a
sorozat 0-hoz tart.
A matematikai vizsgálathoz a homogén lineáris másodrendű
rekurziót kell megoldanunk. Ezt most nem részletezzük, az eredmény fn
= 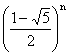 .
.
(Egyébként ha már megsejtettük az explicit alakot, teljes
indukciót is alkalmazhatunk. Segítségével könnyen bizonyítható az állítás, csak
azt kell belátni, hogy 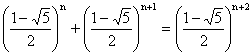 .)
.)
Olyan mértani sorozatot kaptunk, amely kvóciensének 1-nél
kisebb az abszolútértéke; vagyis a sorozat valóban 0-hoz tart.
Előző fejezet
Következő fejezet
Tartalom
![]() vagy a kiíró utasítás
háromszöge: Δ.
vagy a kiíró utasítás
háromszöge: Δ.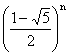 .
.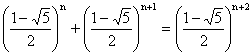 .)
.)