Az alábbiakban egy olyan problémakörrel foglalkozunk – a gépi számábrázolással - , amely a számológépek kezelésekor komoly gondot okozhat, s amely probléma, sajnos, nem kerülhető el.
Fontos kihangsúlyozni, hogy e probléma a legnagyobb kapacitású és teljesítményű számítógépek esetében is jelentkezik.

1. példa:

Ha az utolsó feladat sorozatának későbbi tagjait is kiíratjuk, meglepő dolgot tapasztalunk:

Casio gépen:

,          ,       ,

,         ,

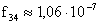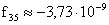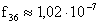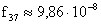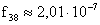majd ezután a sorozat tagjai rohamosan növekedni kezdenek. Pl.

,      ,      ,

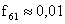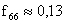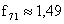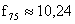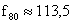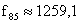,    ,    stb.

Texas gépen ugyanez:

,         ,       ,

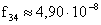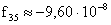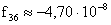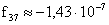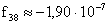,        stb.,

majd

,                ,                ,

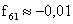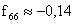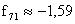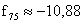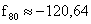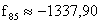,              ,            stb.

Mi lehet ennek az oka?

2. példa:

Ha esetleg arra gondolunk, hogy a programunkban van a hiba, számoljuk ki a kalkulátor sorozat-kezelő menüjével is az értékeket!
(A Casio gépen hívjuk meg a főmenü RECUR menüpontját, a Texas gépen a List menüpontot.)
Itt a kalkulátor segítségével vizsgáljuk meg ugyanezt a rekurziót (ha az (1 – √5)/2-es kezdőértéket kifejezésnek értelmezi a gép, s ezért nem tudjuk bevinni, akkor érdemes pl. egy (1 – √5)/2 →D értékadás után D értékét beolvasni).
Azt tapasztaljuk, hogy itt is végtelenbe tart a sorozat.

3. példa:

Futtassuk le a prímkereső programunkat pl. P = 11111111111 értékkel (11 darab 1-es). Meglepőt állít a gépünk: ez a szám nem prím, mert osztható 5-tel.

4. példa:

Vegyük ki a születésnap-paradoxon programjából a futást nagyon lassító kiíró utasításokat!

Casio gépen:

Texas gépen:

Így lefuttatva a program akkor állhatna meg, ha P = 0 lenne, vagyis N = 367. (Ez természetes, hiszen 366 ember esetén még előfordulhatna, hogy mindegyik ember más-más napon született.)

Ha a program futása után kiírjuk N értékét, meglepő módon az N = 323 értéket kapjuk.

Elég ennyi a meglepetésekből, ideje megmagyarázni a fenti jelenségeket.

Minden számítógép véges sok helyiértéken, 2-es számrendszerben tárolja a számokat. Ebből következik a gépi számhalmaz néhány speciális tulajdonsága:
- 2-es számrendszerbeli racionális számok egy speciális részhalmazáról van szó;
- a halmaz nem folytonos, nem sűrű, de korlátos;
- a számok között létezik maximális és minimális (≠0) abszolút értékű (Max,Min);
- az alapműveletek nem zártak, nincs asszociativitás és disztributivitás stb.

Feltétlenül tisztában kell lennünk azzal, hogy a szám fogalma háromféleképpen is megjelenik a programozás folyamán:
1. amire mi gondolunk (pl. (1 –√5)/2);
2. amit a gép tárol (egy közelítő érték);
3. amit a gép kiír (10 jegy pontosság, az utolsó jegy kerekített).

Az 1. példa meglepetése azért történt, mert f₁-et pici d hibával tárolta a gép. Az összeadások esetében a hibák továbbterjedtek, így f₂-ben megjelent a d, f₃-ban 2d, f₄-ben 3d stb; d-re egy Fibonacci-sorozatot kaptunk. S ez exponenciálisan nő, ráépül az eredeti sorozatra, ami persze a 0 helyett a végtelenhez tart.

A 3. példa az előzőek alapján már érthető: 11 értékes jegyet nem képes kezelni a gép.

(Megjegyzés: Ennek ismeretében viszont igazi csemege az fPart (törtrész) függvény „viselkedése”. Ugyanis fPart(11111111111/5) = 0,2 (helyesen), s így a prímteszt-programban az int(P/I) ≠ P/I sort fPart(P/I) = 0-ra cserélve jól működő prímtesztet kapunk. Persze 15 darab 1-esre már ez sem ad helyes eredményt.)

A 4. példa az alulcsordulás jelensége. A legkisebb, pozitív abszolútértékű, a gép által még ábrázolni tudott Min számnál kisebb számot a gép 0-nak tekint.

Konklúzió: Ezek a problémák elvi jellegűek (tehát nem kiküszöbölhetők ki), ezért a gép használata közben fontos ismernünk gépünk korlátait is.