4. Királylány-probléma
4.1. feladat:
Három
herceg, A, B és C egyaránt szerelmes Bergengócia királylányába. Elhatározzák,
hogy egyetlen pisztolypárbajban eldöntik, melyikük legyen a kérő. Egyszerre
körbeállnak és bármelyikük lőhet bármelyikükre. Tudják egymásról, hogy ha lő, A
1, B 0,8 és C 0,5 valószínűséggel talál, ezért abban állapodnak meg, hogy először
lő C, utána (ha életben van) B, végül A. Ha nincs vége a párbajnak, akkor még
egy kört lőnek azonos sorrendben.
Mikor a királylány meghallotta a
feltételeket, a párbaj előtti este titokban kicserélte C első golyóját
vaktöltényre.
a) Kibe szerelmes a
királylány?
b) Hogyan változnak meg a
párbaj valószínűségei, ha most a felek nemcsak kettő, hanem tetszőleges számú
lövést adhatnak le?
(A királylány most is csak az
első golyót cseréli ki vaktöltényre.)
Megoldás:
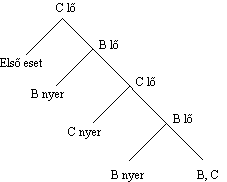
1. eset: Nézzük azt az
esetet, amikor megtörtént a csere, tehát C első golyója vaktöltény. Az első
lövésből C nem talál, B következik. Ő nyilván A-ra lő (mert ha C-re lőne, és őt
véletlenül eltalálná, akkor A következik; A lelövi B-t és nyert). Ha B
eltalálja A-t, akkor a játék "kétszemélyes" lesz B és C között; míg
ha B nem találja el A-t, akkor A következik lövésre. Ő a két lehetséges
ellenfele közül nyilván a veszélyesebb B-re lő, akit el is talál, így ismét
"kétszemélyes játékot" kaptunk A és C között. A teljes játék
folyamatábrája:
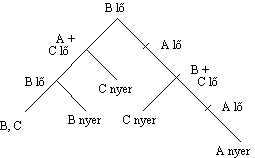
Mekkora valószínűséggel győznek
az egyes párbajozók?
P(A nyer)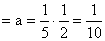 ,
, 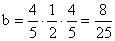 (és
B élve marad további
(és
B élve marad további 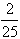 eséllyel, ez a B-C
döntetlen párbaj eredménye),
eséllyel, ez a B-C
döntetlen párbaj eredménye), 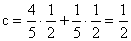 (és C élve marad
további
(és C élve marad
további 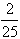 eséllyel, a döntetlen
miatt).
eséllyel, a döntetlen
miatt).
2. eset: Vizsgáljuk most
meg azt a helyzetet, amikor C első lövése nem vaktöltény!
Első lövésével C nyilván A-ra
lő; ha nem találja el, előáll az első eset, míg ha talál, akkor B és C között
egy kétszemélyes párbajt kapunk (amely meglehetősen előnyös B-nek, hiszen ő lő
először, nagyobb valószínűséggel talál, és két lövési lehetősége van, míg C-nek
csak egy). A folyamatábra:
P(A nyer)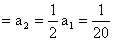 ,
, 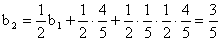 ,
, 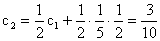 ,
valamint B és C egyaránt élve marad a döntetlen lehetősége miatt
,
valamint B és C egyaránt élve marad a döntetlen lehetősége miatt 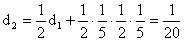 eséllyel.
eséllyel.
|
Az egyes játékosok
(a = 1, b = 0,8, c = 0,5)
|
A győzelmi
valószínűségek vaktölténnyel
|
A győzelmi
valószínűségek éles tölténnyel
|
|
|
|
|
|
A
|
10 %
|
5 %
|
|
B
|
32 %
|
60 %
|
|
C
|
50 %
|
30 %
|
|
döntetlen B és C
között
|
8 %
|
5 %
|
Nos, kedves Olvasó, kibe
szerelmes a királylány? Bármily meglepő, lehet, hogy C-be, hiszen győzelmi
esélye 20%-kal megnőtt. De az is elképzelhető, hogy A-ba, hiszen neki a
beavatkozás után kétszeresre nőtt a győzelmi esélye.
Megjegyzések:
1. Az általános eset
folyamatábrája a, b, c valószínűségekkel, ha C első golyója vaktöltény:
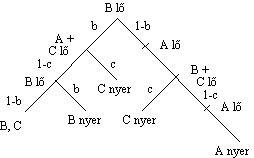
Ennek alapján ha C első golyója
vaktöltény, a nyerési esélyek az alábbiak:
A nyer: a1 = (1 – b)(1 – c);
B nyer: b1 = b2(1 – c);
C nyer: c1 = c;
D (döntetlen): d1 = b(1 – b)(1 – c).
Hogyan néz ki a folyamatábra
akkor, ha az első golyó nem vaktöltény?
A folyamatábra:
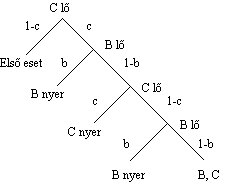
Ha C első lövésével A-t veszi
célba, és golyója nem vaktöltény, akkor az alábbi gyözelmi valószínűségeket
kapjuk:
A nyer: (1 – c)a1;
B nyer: (1 – c)b1 + bc + bc(1 – b)(1 – c);
C nyer: (1 – c)c1 + c2(1 – b);
D: (1 – c)d1 + c(1 – c)(1 – b)2.
Nézzük meg, hogyan változnak a
valószínűségek b és c csökkentésével:
|
Az egyes játékosok
(a = 1, b = 0,5, c = 0,3)
|
A győzelmi
valószínűségek vaktölténnyel
|
A győzelmi
valószínűségek éles tölténnyel
|
|
|
|
|
|
A
|
35 %
|
24,5 %
|
|
B
|
17,5 %
|
32,5 %
|
|
C
|
30 %
|
25,5 %
|
|
döntetlen B és C
között
|
17,5 %
|
17,5 %
|
|
Az egyes játékosok
(a = 1, b = 0,8, c = 0,3)
|
A győzelmi
valószínűségek vaktölténnyel
|
A győzelmi
valószínűségek éles tölténnyel
|
|
|
|
|
|
A
|
14 %
|
9,8 %
|
|
B
|
44,8 %
|
58,7 %
|
|
C
|
30 %
|
22,8 %
|
|
döntetlen B és C
között
|
11,2 %
|
8,7 %
|
2. A megoldás folyamán
feltételeztük, hogy a királylány használni tudja a matematikai folyamatábrákat.
Ha C is elég jó matematikus, akkor az egész csere-tranzakció felesleges, mert C
első lövésével úgyis a levegőbe lő.
Előző fejezet
Következő fejezet
Tartalom

![]() ,
, ![]() (és
B élve marad további
(és
B élve marad további ![]() eséllyel, ez a B-C
döntetlen párbaj eredménye),
eséllyel, ez a B-C
döntetlen párbaj eredménye), ![]() (és C élve marad
további
(és C élve marad
további ![]() eséllyel, a döntetlen
miatt).
eséllyel, a döntetlen
miatt).

![]() ,
, ![]() ,
, ![]() ,
valamint B és C egyaránt élve marad a döntetlen lehetősége miatt
,
valamint B és C egyaránt élve marad a döntetlen lehetősége miatt ![]() eséllyel.
eséllyel.

