5. Geometriai valószínűség paradoxonai

Első megoldás:

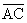
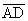
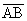
Jelöljük a mozgó pontokat C-vel és D-vel, s legyen az ívek hossza = x, = y. (Persze = rπ.) Ekkor x és y a [0, rπ] intervallumban tetszőleges értékek lehetnek. Az 1.13. és 1.14. feladatokban látott módszer alapján feleltessük meg a C és D pontok helyzetét a sík (0, 0), (0, r), (r, 0), (r, r) négyzete (x, y) pontjának; az (x, y) pont véletlenszerű kiválasztása ekvivalens a C, D pontok kiválasztásával.

A kedvező pontokra teljesülnie kell az 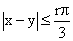egyenlőtlenségnek.

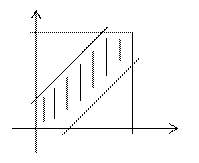
A keresett valószínűség a két terület hányadosa; átalakítások után a kapott érték .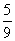

Második megoldás:

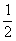
A CD húr F felezőpontja egyértelműen meghatározza a húrt s így a CD távolságot is. A húrfelezőpontok lehetséges helyzetét a két szélső helyzet segítségével határozhatjuk meg. Legyen az AB húr felezőpontja O. Az A-ból, ill. B-ből kiinduló húrok felezőpontjai az AO, ill. OB átmérőjű félkörívek (ui. az A, ill. B pontokból arányú kicsinyítést alkalmazhatunk). Kövekezésképpen az F pont ezen félkörök és az AB félkör közötti részre eshet, ezen alakzat területe . 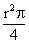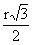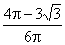Rövid számolással adódik, hogy a kedvező pontok helyzetét egy további sugarú kör korlátozza, s innen a keresett valószínűség ≈ 0,391.

Megjegyzés:

A két érték nem egyezik meg. Melyik megoldás a jó?

Első megoldás:

Az A pontból kiinduló húrok közül csak azok lesznek jók, amelyek belemetszenek a háromszögbe (ábra).

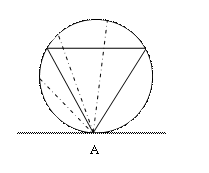
Ennek valószínűsége, mivel a háromszög A-nál levő szöge 60°-os, .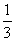

Második megoldás:

Adott (az ábra szerinti függőleges) irányú átmérőre merőleges húrok közül az AB szakaszon áthaladók lesznek az esemény szempontjából kedvezők.

A keresett valószínűség .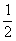

Harmadik megoldás:

A húrok felezőpontjait tekintve a kör belső pontjai szolgáltatják az összes lehetséges esetet, míg egy koncentrikus, feleakkora sugarú kör pontjai a kedvező eseteket. A keresett valószínűség értéke .

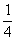
Megjegyzések:

1. Három különböző eredményt kaptunk, melyik tekinthető az „igazinak”?

2. Hogy melyik a helyes válasz, az attól függ, hogy hogyan rajzoljuk meg a véletlen húrt. A három, fent tárgyalt elméleti módszer közül kézenfekvőnek látszik a gyakorlat segítségével kiválasztani a valódi eljárást.
Vagyis konstruáljunk egy modellt, hajtsuk végre elég sokszor a kísérletet, s a tapasztalat megmutatja, melyik megoldás volt a helyes gondolat.

3. De mindhárom eljárás megvalósítható a gyakorlatban.
Az első esetben feltettük, hogy a húr másik végpontjaként szóba jövő pontok egyenletesen oszlanak el a kör kerületén. Ez megvalósítható egy, a körrel koncentrikus pörgettyű segítségével.
A második esetben [6]-ban a szerző azt javasolja, hogy pl. a járdára rajzolt körhöz elég nagy távolságból gurítsunk egy seprűnyelet.
Végül a harmadik esetben pl. vizsgálhatjuk azt, hogy egy melasszal bekent körlemez mely pontjára száll le egy légy.

Vagyis ebben a feladatban mindegyik válasz jó, de mindegyik más-más eljárás esetén.

4. A paradoxonok jelentős része a fenti okok miatt lép fel; vagyis azért, mert nem tisztázzuk a feladat elején, hogy mit is értünk véletlenszerű kiválasztáson.

Első megoldás:

A számegyenes [0, 10] szakaszának a felét tekinthetjük, az eredmény .

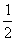
Második megoldás:

A [0, 10] intervallum számai és azok négyzete között kölcsönösen egyértelmű hozzárendelést létesíthetünk. A probléma ugyanaz, mintha azt vizsgálnánk, hogy egy [0, 10] intervallumbeli szám négyzete mikor lesz a [0, 100] intervallum [0, 25] részén; s ennek a valószínűsége már csak .

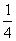
Megjegyzés:

Hogyan oldható fel az ellentmondás?

Megjegyzések:

- Fentebb láttuk, hogy a valószínűség értéke attól függ, hogy milyen mennyiségekkel jellemezzük a háromszöget, ill. a háromszög kiválasztását.
- Különböző mennyiségeket azért választhatunk a jellemzés alapjául, mert különböző eseményeket tekintünk egyenlően valószínűeknek.
- Hogy mely események egyformán valószínűek, néha csak kísérlettel dönthetők el.
- (S néha azzal sem.)

Erre a feladatra 11 megoldási lehetőséget mutatunk.

Első megoldás:

Rögzítsük a középső oldalt! Ekkor p = 0,18.

Második megoldás:

Rögzítsük a maximális oldalt, ekkor p = 0,36.

Harmadik megoldás:

(Egységnyi kerületű) körvonalon az A pontot fixáljuk, a másik két pontot véletlenszerűen választjuk: p = .

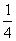
Negyedik megoldás:

Legyen a háromszög beírt körének kerülete 1, az A érintési pont fix, s ehhez választjuk a B, C érintési pontokat: p = .

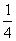
Ötödik megoldás:

Válasszuk ki a maximális szöget! Az összes lehetőség [60°, 180°] közé esik; a kedvező esetek száma a [60°, 90°] intervallum: p = .

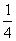
Hatodik megoldás:

Adott kerületű háromszögeket vizsgáljunk.

Megjegyzés:

Lásd 1.13. feladatot!

Hetedik megoldás:

Ugyanezt megtehetjük a trilineáris koordináta-rendszerben is.

Nyolcadik megoldás:

A koordinátasík egységnyi oldalú négyzetében az x és y koordináták véletlenszerű választásával két pontot jelölünk ki (a harmadik csúcs az origó): p = .

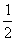
Kilencedik megoldás:

Ugyanúgy járunk el, mint az előző feladatban, csak most mindhárom pontot az egységnégyzetből választjuk: p = .

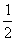
Tizedik megoldás:

Az x + y + z = π a térbeli koordináta-rendszerben egy sík egyenlete. Az első térnyolcadban metszete egy szabályos háromszög, melynek középháromszöge a jó pontok halmaza: p = .

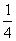
Tizenegyedik megoldás:

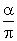
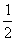
Legyen végül az α hegyesszögű szögtartomány csúcsa A, az egyik szögszáron fix pont B. A B ponton átmenő egyenes forgatásával p = , vagyis p bármilyen, -nél kisebb pozitív szám lehet (α-tól függ).

Megjegyzés:

Középiskolás diákok a kitűzött feladatra néha egy-egy szimulációs programmal válaszolnak, általában a 9. megoldás technikáját alkalmazzák. Egy futási eredmény: 30000 szimulációból 8244 lett a hegyesszögű, 21756 a nem hegyesszögű háromszög. A relatív gyakoriság 0,275.