6. A valószínűség tranzitivitása

Egy ρ reláció tranzitív, ha A ρ B és B ρ C esetén A ρ C is teljesül; ilyen pl. a rendezést létrehozó < vagy ≤ reláció. Ebben a fejezetben arra mutatunk néhány példát, hogy a „nagyobb valószínűség” nem tranzitív reláció; vagyis ha az A esemény valószínűbb, mint a B, valamint a B valószínűbb, mint a C, ebből még nem következik, hogy az A esemény valószínűbb, mint a C.

6.1. példa:

Mindannyian ismerjük a kő - papír - olló játékot: a papír becsomagolja a követ, az olló elvágja a papírt, de kicsorbul a kövön. Ez a három objektum nem rendezhető, nem állapítható meg közöttük erősorrend, ebben a játékban ún. „körbeverés” történik. Ha két játékos úgy játszik, hogy előbb az egyik, majd a másik választ magának egy-egy objektumot, az elsőnek választó játékos hátrányos helyzetben van, hiszen bármelyik objektumhoz található a játék szempontjából nála jobb.

6.2. feladat:

Egy társaságban háromféle rétest lehet választani: almást, meggyest és túróst. Lehetséges-e, hogy bár többen szeretik az almást, mint a meggyest, és többen szeretik a meggyest, mint a túróst, ennek ellenére többen szeretik a túróst, mint az almást?

Megoldás:

Lehetséges, már három ember esetén is. Legyen a három ember „rétes-kedvelési sorrendje” (a, m, t), (m, t, a), (t, a, m), ekkor előáll a kérdezett helyzet.

Megjegyzések:

1. Természetesen több ember esetén is adható konstrukció.

2. Ebben a helyzetben bármelyik fajta rétest is szolgálják fel, a tagok többsége jobbat is kaphatna.

3. Azt az észrevételt, hogy a valószínűség fogalma nem tranzitív, statisztikai megfontolásokkal (gyakoriságok) támaszthatjuk alá, s ezek a problémák a statisztikában is megjelennek, lásd pl. a 8. fejezet problémáit.

6.3. feladat:

András és Béla a következő kockajátékot játsszák. András dobókockáján a 2, 2, 2, 5, 5, 5; Béla kockáján a 3, 3, 3, 3, 3, 6 számok vannak. Mindkét játékos feldobja saját kockáját, s az nyer, aki nagyobbat dobott. Kinek előnyös a játék?

Megoldás:

A 2.10. és 2.11. feladatokban jeleztük, hogy nem az egyes számok abszolút nagysága, hanem egymáshoz viszonyított relatív nagysága a döntő. A 36 lehetőség közül 21 eset kedvező Bélának, így a játék neki előnyös.

6.4. feladat:

Készítsünk nem-tranzitív három dobókockát, pl. a hagyományos 1, 2, 3, 4, 5, 6 számokból! (Nem kell mindegyik számot felhasználni.)

Megoldás:

A kérdés tulajdonképpen az, hogy lehet-e három kockát úgy megszámozni, hogy azok „körbeverjék” egymást? Egy lehetséges megoldás pl. az alábbi:

I: 2, 2, 2, 2, 5, 5; II: 4, 4, 4, 4, 1, 1; III: 3, 3, 3, 3, 3, 3.

(Nem olyan nehéz rájönni a megoldásra. Ha pl. a III-as kocka 3, 3, 3, 3, 3, 3 számait fixáljuk, a másik két kockát pedig I: a, a, a, a, b, b, ill. II: c, c, c, c, d, d alakban keressük, akkor a < 3, b > 3, valamint c > 3, d < 3 feltételek mellett (ekkor I-esnél jobb a III-as és a III-asnál jobb a II-es) elég, ha b > c és a > d teljesül.)

Megjegyzések:

1. Átfogalmazhatjuk a problémát két játékos közötti kockajátékra. Ekkor az I, II vagy III-as kockából választ egyet-egyet a két játékos, s az nyer, aki nagyobbat dob. Ekkor a játék a másodiknak választó játékos számára előnyös.

2. A „körbeverés” jelenségét nevezik rendezési paradoxonnak.

További feladatok

6.5. feladat:

Három játékos, A, B, C játékában három hosszú érmedobás-sorozatot vizsgálunk. Egy szabályos érmét folyamatosan dobálnak a játékosok úgy, hogy a játék szempontjából mindig csak az utolsó három dobás eredményét veszik figyelembe. (Egy lehetséges játék lenne pl. a következő: A nyer, ha az utolsó 3 dobás az FFF célsorozat, B nyer, ha III, C nyer, ha IFI.) A szabály ebben a játékban a következő:

Először az A játékos választ egy három-hosszú sorozatot, ez lesz az ő célsorozata; ezután B választ egy célsorozatot úgy, hogy A-val szemben ez a lehető legjobb legyen számára; majd C választja azt, amelyik számára B-vel szemben a lehető legelőnyösebb. A játékosok által befizetett tét játékonként és fejenként 12 egység. Ez a játék A számára nagyon előnytelennek tűnik, ezért ha B vagy C nyer a játékban, akkor fájdalomdíjként a 36 egység nyereményből 3 egységet átad A-nak.

Kinek legelőnyösebb így ez a játék? Hogyan kezdjen A?

Útmutatás:

A Markov-láncok témakörénél (link) ez volt a 6.13. feladat. Itt megadtuk a kétszemélyes, háromdobásos érmedobálási játékok esélyeit tartalmazó táblázatot, ezt most is közöljük:

 

FFF

FFI

FIF

FII

IFF

IFI

IIF

III

FFF

–

1:1

2:3

2:3

1:7

5:7

3:7

1:1

FFI

1:1

–

2:1

2:1

1:3

5:3

1:1

7:3

FIF

3:2

1:2

–

1:1

1:1

1:1

3:5

7:5

FII

3:2

1:2

1:1

–

1:1

1:1

3:1

7:1

IFF

7:1

3:1

1:1

1:1

–

1:1

1:2

3:2

IFI

7:5

3:5

1:1

1:1

1:1

–

1:2

3:2

IIF

7:3

1:1

5:3

1:3

2:1

2:1

–

1:1

III

1:1

3:7

5:7

1:7

2:3

2:3

1:1

–

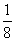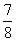Itt pl. az IFF sor FFF oszlopában lévő 7:1 arány azt jelenti, hogy az érmét folyamatosan dobálva annak valószínűsége, hogy előbb jön ki FFF, mint IFF, , míg annak a valószínűsége, hogy hamarabb kapunk IFF-et, . (Lsd. 2.7. feladat.)

6.6. feladat (egy érmedobálás-paradoxon):

Egy érmét folyamatosan feldobálva az FFI, IFF, IIF, FII sorozatok egyaránt átlagosan 8 dobás után jönnek ki. Hasonlítsuk össze ezt a négy esetet abból a szempontból, hogy melyiknek van nagyobb esélye arra, hogy korábban előforduljon. Haladjunk a kisebb valószínűségű esemény felé, legyen a sorrend FFI – IFF, IFF – IIF, IIF – FII (lásd előző táblázat). Tapasztalunk valami érdekeset?

Előző fejezet    Következő fejezet    Tartalom