I/19. feladatának megoldása:
A 10. feladatban a háromról csak annyit használtunk fel, hogy páratlan, tehát általában is igaz, hogy:
Ha n páratlan és d is, akkor nincs n pontú, d-reguláris gráf.
Ha ugyanis volna, akkor minden pontból d él indulna ki, ez nd él, de így minden élt kétszer számoltunk, tehát az élszám nd/2 volna, s ez nem egész szám, ami lehetetlen.Ha viszont n és d közül legalább az egyik páros, akkor már van n pontú d-reguláris gráf.
Egy ilyet a következő képpen lehet csinálni. Legyen eloször
n tetszőleges és
d=2
D páros. Képzeljük most egymást nem ismerő embereknek a gráf pontjait, és ültessük le őket ismét egy kerek asztal köré. Ismertessünk össze mindenkit a tőle jobbra és balra 1, 2, …,
D távolságra ülőkkel. Ha például
d=6 (
D=3), akkor mindenkit összeismertetünk a bal és jobb oldali szomszédjával, másodszomszédjával és harmadszomszédjával. Így mindenkinek pontosan 2
D ismerőse lesz. (Meg kell még gondolnunk, hogy ha egy
E embert bemutattunk egy
E’ embernek, akkor
E’-t is bemutattuk
E-nek, különben nem lennének kölcsönösek az ismeretségek, tehát nem beszélhetnénk – irányítatlan – gráfról.) Mindez persze csak akkor megy, ha az a 2
D ember, akit így sorra veszünk, mind különböző, vagyis ha
n>2
D, azaz
n legalább
d+1.Ha rögtön gráfelméleti nyelven akarjuk elmondani a konstrukciót, akkor mondhatjuk a következőt: Legyenek a gráf pontjai egy szabályos
n-szög csúcsai, és számozzuk meg őket 1-tol
n-ig:
P1,
P2, …,
Pn, és egyezzünk meg abban, hogy
Pn+1=
P1,
Pn+2=
P2, s általában
Pn+k=
Pk. Kössünk össze két pontot, ha a sorszámuk különbsége 1, 2, …,
D. (Így például
P1 össze lesz kötve
P2-vel,
P3-mal, ….,
PD+1-gyel, de össze lesz kötve
Pn-nel,
Pn–1-gyel, …,
Pn–D+1-gyel is (mert
P1=
Pn+1). Így minden pont fokszáma éppen 2
D lesz. Megint fel kell tenni, hogy
n legalább
d+1 és megint meg kell gondolni, hogy ha egy
Pi pontot összekötöttünk egy
Pk ponttal, akkor a
Pk pontot is összekötöttük a
Pi ponttal.
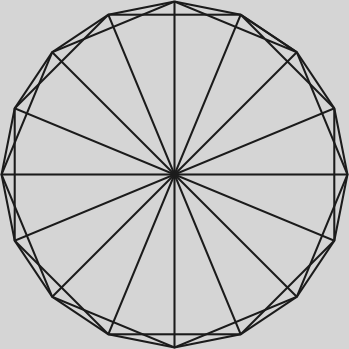
Marad az az eset, ha n=2m páros, d páratlan. Ekkor d–1=2D páros, tehát megcsinálhatjuk az eloző konstrukciót, majd még minden pontot összekötünk a vele szemben levővel, vagyis az i-ediket az m+i-edikkel. Itt persze fel kell tennünk, hogy ezzel a ponttal még nem volt összekötve, tehát hogy m>D, azaz n=2m>2D, vagyis n legalább 2D+2=d+1. (Az ábra D=2-re mutatja a gráf egy darabját.) Összefoglalva azt kapjuk, hogy ha nld+1 és n és d közül legalább az egyik páros, akkor van (egyszerű) n pontú d-reguláris gráf, ha viszont n is, d is páros, akkor nincs.
