17. feladat:

Egy társaságban öt házaspár van jelen. Azok, akik nem ismerik egymást, bemutatkozásul kezet fognak egymással. Kovács úr megkérdezi minden jelenlevőtől, hogy hány emberrel fogott kezet és csupa különböző számot kap válaszul. Hány emberrel fogott kezet Kovácsné? És Kovács úr?
Az összes feladat megoldása

18. feladat:

Egy három házaspárból álló társaság együtt vacsorázik egy étteremben. A társaság minden tagja külön-külön érkezik és kezet nyújt a jelenlevőknek, kivéve saját házastársát. Amikor mind a hatan megérkeztek, Kovácsné  megkérdezi a többiektől, ki hány embernek nyújtott kezet, és mindenkitől más számot kap válaszul. Hanyadiknak érkezett Kovácsné?
Az összes feladat megoldása

19. feladat(a 10. feladat folytatása):

d-reguláris gráfnak neveztük az olyan gráfot, amelyben minden pont foka pontosan d. Milyen n-ekre van n pontú d-reguláris gráf?
Az összes feladat megoldása

20. feladat:

Bizonyítsuk be, hogy bármely (egyszerű véges) gráfban a páratlan fokú pontok száma páros.
Az összes feladat megoldása

21. feladat:

Egy táncos estén négy fiú és négy lány vett részt. Megkérdeztük a lányokat, hogy hány fiúval táncoltak és a következő válaszokat kaptuk: 3, 1, 2, 2. Megkérdeztük a fiukat is, hogy hány lánnyal táncoltak és a következő válaszokat adták: 2, 2, 3, 2. Mutassuk meg, hogy valaki nem az igazat mondta.
Az összes feladat megoldása

22. feladat:

a)Egy táncos estén 21 fiú és 21 lány vett részt. Minden fiú vagy négy lánnyal vagy két lánnyal táncolt, kivéve egyet, aki hat lánnyal táncolt. Lehetséges-e, hogy minden lány három vagy öt fiúval táncolt?
Az összes feladat megoldása
b)

b)Egy 21 tagú társaságból mindenki két vagy négy másiknak írt levelet, kivéve egyet, aki hat társának írt levelet. Lehetséges-e, hogy mindenki három vagy öt levelet kapott?
Az összes feladat megoldása

23. feladat:

Az előző feladat a) részét egy ún. ' páros gráffal' szemléltethetjük: az olyan gráfot nevezzük páros gráfnak, amelynek csúcsai két osztályba sorolhatók úgy, hogy a gráf minden éle két különböző osztálybeli pontot kössön össze. (Jelen esetben a két csúcsosztály: a fiúk ' osztálya' és a lányok ' osztálya' , minden táncospár egy fiúból és egy lányból áll.)
A feladat b) részét egy irányított gráffal szemléltethetjük: minden levél egy él, amelynek kezdőpontja az, aki írta, végpontja az, aki kapta. A feladat azt sejtteti, hogy az irányított gráfok és a páros gráfok között szoros megfeleltetéses kapcsolat van. Mutassuk meg, hogy ez valóban így is van!
Az összes feladat megoldása

24. feladat:

Egy összejövetelen 21 gyerek vett részt. Mindegyiktől sorra megkérdeztem, hány osztálytársa van a jelenlévők közt. Az első 13 válaszoló közül öten mondtak hármat, nyolcan négyet. Vajon hány osztálytársa volt jelen a többi gyereknek, ha azt tudjuk, hogy mindegyiküknek volt jelen legalább egy osztálytársa?
Az összes feladat megoldása

25. feladat:

Egy tíztagú társaságról tudjuk, hogy minden tagja legalább hét másikat ismer. Igazoljuk, hogy a társaságból bármely három személynek van közös ismerőse.
Hogyan általánosítható a feladat?
Fogalmazzuk meg az általános állítást gráfelméleti nyelven!
Az összes feladat megoldása

26. feladat:

Egy 3n tagú társaságban bármely két embernek van közös ismerőse. A 16. feladatban láttuk, hogy kiválasztható n ember, amelyek együttesen az összes többit ismerik. Kiválasztható-e mindig n-nél kevesebb ember is?
**Van-e olyan pozitív

d, amelyre kiválasztható-e n^{1 dd}

ember is?
**Mutassuk meg, hogy van olyan n pontú gráf, amelyben bármely két pontnak van közös szomszédja, és amelyben bármely (n/2)^1/2 1 ponthoz van olyan pont, amellyel egyikük sincs összekötve.

27. feladat:

a)Egy egyszerű véges gráfról a következőket tudjuk: bármely két össze nem kötött pontjának van közös szomszédja, semely két összekötött szomszédjának nincs közös szomszédja. Következik-e ebből, hogy a gráf reguláris?
Az összes feladat megoldása
b) Mi a helyzet, ha azt is megköveteljük, hogy a gráfban ne legyen telített pont, vagyis olyan pont, amelyik minden más ponttal össze van kötve?
Az összes feladat megoldása
c)* Mi a helyzet, ha azt is megköveteljük, hogy a gráfban ne legyen telített pont és azt is, hogy ha két pont nincs összekötve, akkor pontosan egy közös szomszédjuk legyen?
Az összes feladat megoldása
d)** ' Barátság-probléma' : Egy társaságban bármely két embernek pontosan egy közös ismerőse van. Igaz-e, hogy vagy mindenkinek azonos számú ismerőse van, vagy van olyan ember, aki a társaság minden tagját ismeri?
Az összes feladat megoldása

28. feladat:

Van-e olyan, a teljes gráftól különböző 49 pontú gráf, amelyben bármely két pont közös szomszédainak száma páratlan?
*Van-e ilyen tulajdonságú 50 pontú gráf?
Az összes feladat megoldása

29. feladat:

(OKTV 1986. I. kategória, döntő) Egy üdülő bármely három lakója között van kettő, aki nem ismeri egymást, de bármely hét között van legalább kettő, aki ismeri egymást. Az üdülés befejeztével mindenki megajándékozza minden ismerősét egy-egy ajándéktárggyal. Bizonyítsuk be, hogy n lakó esetén legfeljebb 6n ajándéktárgyat adtak át.
Fogalmazzuk át az állítást gráfokra!
Az összes feladat megoldása

30. feladat*:

Az elmúlt évben a világranglistán nyilvántartott teniszezők átlagosan 30 ellenféllel játszottak. Következik-e ebből, hogy kiválasztható közülük néhány úgy, hogy ha csak az ezeknek egymás ellen játszott mérkőzéseit nézzük, mindenki legalább 16 másikkal játszott?
Milyen gráfelméleti állítást mondhatunk ki a válasz alapján?
Az összes feladat megoldása

31. feladat:

a) Minimálisan hány éle van egy olyan tíz pontú gráfnak, amelynek bármely öt pontja között legalább két él fut?
Az összes feladat megoldása
b) Minimálisan hány éle van egy olyan n pontú gráfnak, amelynek bármely öt pontja között legalább két él fut?
Az összes feladat megoldása

32. feladat*:

Egy poliéder minden csúcsára egy-egy egész számot akarunk írni úgy, hogy ha két csúcs élszomszédos, akkor a rájuk írt számoknak legyen egynél nagyobb közös osztójuk, ha nem élszomszédosak, akkor ne legyen. Lehetséges-e ez minden egyszerű poliédernél?
Mi a helyzet ha a követelmény fordított: két csúcson szereplő szám pontosan akkor legyen relatív prím, ha él köti össze őket?
Az összes feladat megoldása

33. feladat:

Egy gráf minden csúcsára egy-egy számot írunk (különböző csúcsokra nem feltételenül különbözőt; a feladat szempontjából az is elég, ha minden csúcsra nullát vagy egyet írunk). A csúcsokon szereplő számok összege legyen S. Ezután minden csúcsra ráírjuk azt a számot, amelyet úgy kapunk, hogy S-ből kivonjuk a csúcs szomszédain álló számok összegét. A kérdés az, hogy az utóbbi számok között hány páratlan lehet, ha
a) a tetraéder,                    b) az oktaéder              c) a kocka

d) az ikozaéder gráfjáról van szó?
Az összes feladat megoldása

34. feladat**:

Egy társaságot  vegyes' társaságnak nevezünk, ha sem olyan nincs benne, aki mindenkit ismer, sem olyan, aki senkit nem ismer. (Az ismeretségek kölcsönösek.) Bizonyítsuk be, hogy ha egy  legalább öttagú  társaság  vegyes' , akkor kiválaszthatók közülük négyen olyanok, akik egymás között  vegyes' társaságot alkotnak.
Az összes feladat megoldása

35. feladat*:

Az erdőben 12 törpe él piros vagy kék házikóban. Minden év i-edik hónapjában az i-edik törpe felkeresi összes barátját, hogy eldöntse, átfesse-e a házát. Akkor és csak akkor fogja átfesteni (pirosról kékre vagy fordítva), ha a barátai többsége másszínű házban lakik, mint ő. Bizonyítsuk be, hogy néhány év után már senki nem festi át házikóját. (A barátságok kölcsönösek és az évek során nem változnak.)  (1990 Arany Dániel verseny, haladó, tagozatos kategória, döntő 2.)
Az összes feladat megoldása

36. feladat*:

Egy értekezletre két delegáció érkezik, A és B, mindkettőnek ugyanannyi tagja van. A két delegáció tagjai közt némelyek már ismerik egymást. Bizonyítsuk be, hogy az A delegációból kiválasztható néhány ember (legalább egy) úgy, hogy a B delegáció minden tagja páros sokat ismer a kiválasztottak közül, vagy úgy, hogy minden tagja páratlan sokat ismer a kiválasztottak közül.
Az összes feladat megoldása

37. feladat**:

Mutassuk meg, hogy minden gráf csúcsai két részre vághatók úgy, hogy a pontoknak a saját osztályukban páros sok szomszédjuk van. (Vagyis a két osztály által feszített két részgráfban minden pont foka páros.)
Az összes feladat megoldása

38. feladat**:

Egy 3n + 1 tagú társaság bármely két tagja vagy teniszezni, vagy sakkozni, vagy pingpongozni szokott egymással. Mindegyiküknek n tenisz-, n sakk- és n pingpongpartnere van.
Bizonyítsuk be, hogy van a társaságban három olyan ember, akik egymás között mind a három játékot játsszák. Kürschák J. verseny, 1987
Az összes feladat megoldása

39. feladat*:

Három iskola mindegyikébe n tanuló jár. Minden tanuló a másik két iskolából együttvéve n+1 tanulót ismer. Bizonyítsuk be, hogy választható a három iskola mindegyikéből egy-egy tanuló úgy, hogy mindhárman ismerik egymást. (Az ismeretségeket kölcsönösnek tételezzük fel.) Kürschák J. verseny, 1977
Az összes feladat megoldása

40. feladat*:

Egy n pontú egyszerű gráf csúcsainak fokszáma nagyság szerinti sorrendben d₁

£d₂£ £d_n. Bizonyítsuk be, hogy minden i-re igaz, hogy d_i+1+d_i+2+& +d_n ³ d₁+d₂+& +d_i i(i 1)/2.
Az összes feladat megoldása

41. feladat*:

a) Melyik az a legkisebb n, amelyre van n pontú egyszerű gráf, amelyben nincs telített pont és nincs izolált pont sem?
Az összes feladat megoldása
b) Hány olyan gráf van, amelynek csúcsai az 1, 2, 3, 4 számok, s amelyekben sem telített pont, sem izolált pont nincsen?
Az összes feladat megoldása
c) Tekintsük azokat a gráfokat, amelyeknek csúcsai az 1, 2, & , n egész számok és n legalább kettő. Bizonyítsuk be, hogy ezek között páros az olyan gráfok száma, a melyekben sem telített pont, sem izolált pont nincsen.
Az összes feladat megoldása
d) Tekintsük azokat a gráfokat, amelyeknek csúcsai az 1, 2, & , n egész számok, s amelyekben nincsen telített pont. Legyen T_n az ilyen gráfok száma. Milyen n-ekre páros T_n?
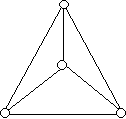
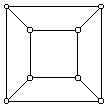
Az összes feladat megoldása