I/27c) feladat megoldása:

c) viszont igaz: ha egy gráfban nincs telített pont, bármely két össze nem kötött pontnak pontosan egy közös szomszéda van, összekötött pontoknak nincs közös szomszédjuk, akkor a gráf reguláris. Most ezt fogjuk bebizonyítani. Először azt bizonyítjuk, hogy ha két pont nincs összekötve, akkor azonos a fokszámuk. Legyen x és y két össze nem kötött pont a gráfban, X és Y legyen x illetve y szomszédainak halmaza. A feltétel szerint X-nek és Y-nak pontosan egy közös pontja van és X-ben, Y-ban nem fut él. Legyen z a közös pont és legyen u X egy tetszőleges, z-től különböző pontja.

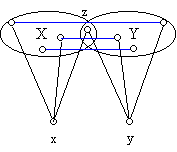
A feltétel szerint u-nak és y-nak pontosan egy közös szomszédja van, tehát u Y-nak pontosan egy pontjával van összekötve és ez a pont nem lehet z (mert X pontjai között nem fut él). Ugyanígy látható be, hogy Y minden, z-től különböző pontja X-nek pontosan egy pontjával van összekötve és ez a pont nem lehet z. Ez azt jelenti, hogy X\{z} és Y\{z} pontjai között a gráf élei egy „matching”-et (egy-egyértelmű megfeleltetést, 1-faktort) alkotnak. Vagyis e két halmaz egyenlő elemszámú. Ezzel beláttuk, hogy x és y foka azonos. Tehát bármely két össze nem kötött pont foka azonos. Ha viszont x és y össze van kötve éllel, akkor van olyan z pont, amellyel egyik sincs összekötve, s ezzel mindkettőnek azonos a foka. Ezzel beláttuk, hogy bármely két pont foka azonos, tehát a gráf reguláris.

HOL A HIBA az elmondott bizonyításban? Hol használtuk ki, hogy nincs a gráfban telített pont? A hiba ott van, hogy feltettük, hogy ha x és y között fut él, akkor van olyan pont, amellyel egyikük sincs összekötve. Ez nem biztos, és nincs is rá szükségünk. Most megmutatjuk, hogy lehet jól befejezni ezt a bizonyítást. Tekintsünk két olyan pontot, amelyek között fut él a gráfban, legyenek ezek x és y. Legyen X x-nek y-tól különböző szomszédai halmaza. Hasonlóan definiáljuk Y-t is. A feladat feltétele szerint e két halmaz diszjunkt és egyiken belül sem fut él. X pontjai nincsenek összekötve y-nal, tehát a már bizonyítottak szerint mindegyikük foka megegyezik y fokszámával. Ugyanígy Y pontjainak fokszáma megegyezik x fokszámával:

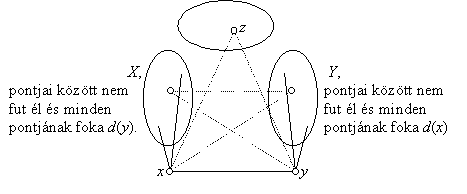
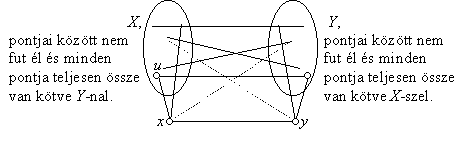
Ha van olyan z pont, amely nincs benne a két halmaz egyesítésében és különbözik x-től és y-tól, akkor a már bizonyítottak szerint z fokszáma egyezik x fokszámával is, y-éval is, tehát x és y fokszáma egyenlő. A továbbiakban feltehetjük, hogy nincs ilyen z, azaz X∪Y∪{x, y} tartalmazza a gráf összes pontját.Ha van olyan u pont X-ben és v pont Y-ban, amelyek között nem fut él, akkor e két pont fokszáma is megegyezik, s ebből már következik, hogy a gráf összes pontjának azonos a fokszáma. Marad az az eset, ha X és Y pontjai között minden él be van húzva:

Ez azt jelenti, hogy X∪{y} és Y∪{x} „teljes páros gráf”: azonos halmazbeli pontok között nem fut él, a két halmaz pontjai között viszont minden él be van húzva. Tegyük fel, hogy X nem üres és legyen u egy pontja. A feladat másik feltétele szerint u-nak és y-nak pontosan egy közös szomszédja van. Tudjuk, hogy x közös szomszédjuk, tehát nincs több közös szomszédjuk. Márpedig Y minden pontja közös szomszédjuk. Ebből következik, hogy Y üres halmaz. De akkor x telített pont, amit a feladat feltétele kizárt. (Itt használjuk ki azt a feltételt, hogy nincs telített pont.)Ezzel bebizonyítottuk az állítást.

MEGJEGYEZZÜK, hogy már tudjuk, hogy bármely két össze nem kötött pont foka egyezik, akkor a bizonyítás talán valamivel egyszerűbben is befejezhető. Ehhez azonban használni kell az összefüggő komponens fogalmát a következő fejezetből: Nyilván elég azt bizonyítani, hogy a komplementer összefüggő. Ez ugyanis pontosan azt jelenti, hogy tetszőleges x és y ponthoz vannnak olyan v1v2…vj pontok, amelyek közül v1 x-szel, vj y-nal nincs összekötve, és vi nincs összekötve vi+1-gyel. De akkor x foka megegyezik v1 fokával, az v2-jével, az v3-éval, stb. végül vj-éval, s az y fokával.Tegyük fel, hogy a komplementer nem összefüggő, tehát a gráf pontjai két nem üres diszjunkt részhalmazra bonthatók, amelyek között a komplementerben nem megy él. Ekkor a két ponthalmaz közötti minden él a gráfban fut. Ha mindkét halmaz legalább kételemű, akkor bármely két pontnak, amely ugyanabban a halmazban van, legalább két közös szomszédja van a gráfban (hiszen a másik halmaz bármely pontja közös szomszéd). Ez azonban ellentmond a feladat feltételének. Tehát legalább az egyik halmaz egyelemű. Ekkor viszont ez a pont az összes többivel össze van kötve, amit szintén kizártunk.