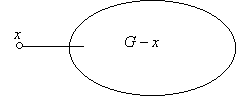SURÁNYI LÁSZLÓ: GRÁFELMÉLET
II. fejezet/1. rész
ÖSSZEFÜGGŐ ÉS KÖRMENTES GRÁFOK, FÁK,
FAVÁZ KERESO ALGORITMUSOK
a) KÖR ÉS ÚT
Először két új fogalmat vezetünk be, a kör és az út fogalmát. Ehhez tekintsük a következő feladatot:
1. feladat:
Egy társaságban mindenkinek van legalább két ismerőse (az ismeretség most is kölcsönös). Bizonyítsuk be, hogy van a társaságban néhány (legalább három) ember, akik leültethetők egy asztal köré úgy, hogy mindenki két ismerőse között üljön. (A társaságnak természetesen véges sok tagja van.)
MEGOLDÁS:
Vegyünk egy tetszőleges embert, legyen ő
A1. Legyen egy ismerőse
A2, legyen továbbá
A2-nek egy
A1-tol különböző ismerőse
A3, és általában legyen
Ak+1-nek egy
Ak-tól különböző ismerőse
Ak+2. Ilyen van, hiszen mindenkinek van legalább két ismerőse. Így kapjuk az embereknek egy
A1A2…
Am… végtelen sorozatát, ahol mindenki ismeri az előtte és utána következőt. Ez a sorozat azonban egy idő után biztosan tartalmaz ismétlődést, hiszen a társaságnak csak véges sok tagja van. Legyen
Am+1 az első olyan ember, aki már szerepelt a sorozatban előbb is, mondjuk az
n-edik helyen:
Am+1=
An (
n<
m). Ekkor
An-et,
An+1-et,
An+2-et, …,
Am-et ilyen sorrendben leültetve az asztal köré mindenki két ismerőse között fog ülni. (Ez igaz
Am-re is, mert
Am+1=
An.)
A feladatot és megoldását átfogalmazhatjuk gráfelméleti nyelvre.
DEFINÍCIÓ:
A gráf csúcsainak egy A1A2…AmAm+1 sorozatát, amelyben minden Ai-t él köt össze az utána következő Ai+1-gyel, a gráf egy sétájának nevezzük.
Ha minden Ai csúcs különböző, akkor útnak nevezzük.
Ha minden Ai különböző, csak Am+1=A1, akkor (gráfelméleti) körnek nevezzük.
Az út, illetve a kör hossza m (vagyis a szomszédos csúcsokat összekötő élek száma), de szokták ehelyett a csúcsok számát is az út, illetve a kör hosszának tekinteni. A kör esetében mindkettő azonos, az út esetében egy a különbség. Megjegyezzük még, hogy a két pontból (tehát egy élből) álló út is út, viszont a legrövidebb körnek is legalább három csúcsa (és három éle) van.
1.a feladat:
Fogalmazzuk át az 1. feladat állítását ezeknek a gráfelméleti fogalmaknak a segítségével!
Az 1. feladat gráfelméleti nyelven a következőképpen szól:
TÉTEL:
1. Ha egy véges egyszerű gráfban minden pont foka legalább ketto, akkor a gráf tartalmaz kört.
Vagy átfogalmazva az állítást:
1’. Ha egy véges egyszerű gráfban nincs kör, akkor van izolált pontja vagy elsőfokú pontja.
Ha egy körmentes gráfból elhagyjuk az izolált pontokat, akkor is körmentes marad. Ha nem csupa izolált pontból áll, akkor marad még pont benne, s ezek között is kell lennie izolált pontnak vagy elsőfokú pontnak. De az izolált pontokat már elhagytuk, tehát van elsőfokú pont a gráfban. A következő állítást kapjuk:
1’’. Ha egy véges egyszerű gráfban nincs kör és van éle, akkor van elsőfokú pontja.
2. feladat:
Bizonyítsuk be az 1. állítás alábbi fontos következményét:
TÉTEL:
Ha egy n pontú egyszerű gráfban nincs kör, akkor legfeljebb n–1 éle van,
azaz:
Ha egy gráfnak legalább annyi éle van, ahány pontja, akkor van benne kör.
A feladat állítását teljes indűkcióval bizonyítjuk.
n=1 esetén a gráfnak nincs éle, n=2 esetén a gráfnak legfeljebb egy éle van.
Tegyük fel, hogy n–1 pontú gráfokra már tudjuk az állítást és legyen G egy n pontú egyszerű, körmentes gráf. Az 1’ állítás szerint G-ben van egy legfeljebb elsőfokú pont (különben G nem körmentes), legyen ez a pont x. Hagyjuk el a G gráfból az x pontot és a belőle (esetleg) induló élt.
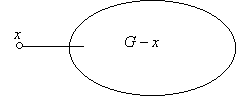
A maradó n–1 pontú gráfban továbbra sincs kör, így legfeljebb n–2 éle van az indukciós feltevés szerint. Ha ehhez hozzávesszük az x-bol induló egyetlen élt (ha van egyáltalán), megkapjuk, hogy G-nek legfeljebb n–1 éle van.
A feladat állítására egy másik bizonyítást is adunk majd (lásd (F)). Ehhez azonban szükségünk lesz pár egyszerű, a körmentes gráfokra vonatkozó állításra és definícióra:
b) A KÖRMENTES ÖSSZEFÜGGŐ GRÁFOKKAL KAPCSOLATOS ALAPVETŐ TÉTELEK ÉS DEFINÍCIÓK
TÉTEL:
(A) Ha egy (egyszerű) gráfban van két pont, amelyek között fut két különböző út (amelyek akár csak egy élben is különböznek), akkor a gráfban van kör.
Vagy másképp fogalmazva:
Egy körmentes gráfban bármely két pont között legfeljebb egy út fut.
3. feladat:
Bizonyítsuk be a fenti (A) állítást!
AZ (A) ÁLLÍTÁS BIZONYÍTÁSA:
Tegyük fel, hogy a gráf A és B pontja között két különböző út indul. Ha e két útnak csak a végpontjaik, A és B a közös pontja, akkor a két utat összerakva máris találtunk egy kört. Ha van a két útnak közös belső pontja is, akkor induljunk el az egyik úton A-ból B-be és menjünk addig, amíg először találunk a másik útnak belső pontjára. Legyen ez a pont C. Forduljűnk vissza a C pontból a másik úton A-ba. Útközben biztosan nem fogjuk az első AC út pontjait érinteni, mert akkor nem C volna az első közös pont. Tehát egy körhöz jutunk.
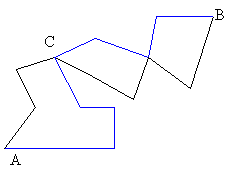
MEGJEGYZÉS:
Az (A) állításnak bizonyos értelemben „párja” a (C) állítás.
TÉTEL:
(B) Ha egy gráf két pontja között van séta, akkor van út is,
másrészt:
ha egy gráfban van A-t és B-t összekötő út és van B-t és C-t összekötő út, akkor van A-t és C-t összekötő út is. Van olyan A-t C-vel összekötő út is, amely csak e két út pontjait és éleit „használja”.
4. feladat:
Bizonyítsuk be a fenti (B) állításait!
(B) ÁLLÍTÁSAINAK BIZONYÍTÁSA:
Az első állításhoz elég meggondolnunk, hogy a két pont közötti legrövidebb sétában nem lehet pontismétlődés, hiszen ha egy pontot többször is érintenénk, akkor a két érintése közötti részt nyugodtan elhagyhatnánk a sétánkból, s továbbra is a két pont közötti sétát kapnánk. (Az ábrán – ahol az élek sorrendjét számozással jelöltük – a kékkel jelölt „hurok” például elhagyható, de a többi él már nem.) Beláttuk tehát, hogy ha két pont között van séta, akkor a legrövidebb séta egyben út is.
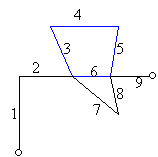
Valójában egy kicsit többet is beláttunk. Legyen a két végpont A és B és vegyünk egy tetszőleges sétát e két pont között. Ha tekintjük azokat a sétákat A és B között, amelyek csak ennek a sétának az éleit tartalmazzák, és kiválasztjuk közülük a legrövidebbet, már az is biztosan út. Ugyanis a fenti eljárással mindaddig hagyhatunk el az eredeti sétából „hurkot”, amíg megszűnnek a pontismétlődések.
Ebből a megjegyzésből viszont már következik (B) második állítása: tekintsük azt a sétát A és C között, amelyet az A-t B-vel összekötő útból, majd a B-t C-vel összekötő útból teszünk össze. Az előbb mondottak szerint A és C közötti út lesz a legrövidebb olyan séta, amely csak ennek a sétának az éleiből áll (tehát csak a két út éleit „használja”).
A második állítás bizonyítására bemutatunk egy másik bizonyítást is, amely egyrészt nagyon hasonlít az előző bizonyításra, másrészt nagyon hasonló a 3. feladat bizonyításához is. Induljunk el az A-ból B-be vezető úton és menjünk addig, amíg az első olyan ponthoz nem érünk, amely rajta van a B-t C-vel összekötő úton is. (Legkésőbb a B pont ilyen lesz.) Ebből a pontból folytassuk az utunkat a B-bol C-be vezető úton C-ig. Útközben biztosan nem találkozunk már érintett ponttal, hiszen D volt az első közös pont. Így kaptunk egy A-t C-vel összekötő utat.
Szükségünk lesz a következő két alapvető definícióra, ezeket lépten-nyomon használjuk a gráfelméletben.
DEFINÍCIÓ:
Összefüggő gráfnak nevezzük azokat a gráfokat, amelyekben bármely két pont között vezet út.
(B) második állítása alapján rögtön adhatunk egy ALTERNATÍV DEFINÍCIÓT is: egy gráfot akkor nevezünk összefüggőnek, ha van olyan X pontja, amelyből az összes többi ponthoz vezet út.
Megjegyezzük, hogy (B) első állítása szerint elég lenne azt megkövetelnünk, hogy egy pontból bármely más pontba vezessen séta.
4a feladat:
Bizonyítsuk be, hogy az összefüggőségre adott két definíció megegyezik!
BIZONYÍTÁS:
Nyilvánvaló, hogy ha egy gráfra teljesül az összefüggőség első definíciója (azaz bármely pontból bármely pontba vezet út), akkor bármely pontja megfelel X-nek a második definícióban: bármely X pontjából vezet út az összes többi ponthoz. Másrészt ha a gráfban van egy X pont, amelyből az összes többi pontba vezet út, akkor legyen Y és Z a gráf két további pontja. X-bol vezet út Y-ba és vezet út Z-be, tehát (B) szerint Y és Z között is vezet út (X játssza B szerepét, Y és Z játssza A és C szerepét).
DEFINÍCIÓ:
Fának nevezzük az összefüggő körmentes gráfokat. (Hogy miért így hívják oket, arra hamarosan fény derül.)
Fa például minden út, ezek a „legkiterjedtebb” fák, másrészt a „legsűrűbb” fa az úgynevezett csillag, amelynek van egy telített pontja, és minden él ebből a pontból indul:
(A) és (B) alapján kimondhatjuk a következőt:
TÉTEL:
(C) Egy gráf pontosan akkor fa (körmentes összefüggő gráf), ha bármely két pontja között pontosan egy út vezet.
5. feladat:
Bizonyítsuk be a fenti (C) állítást!
A (C) ÁLLÍTÁS BIZONYÍTÁSA:
A gráf valóban pontosan akkor fa, ha bármely két pontja között pontosan egy út vezet. Ugyanis pontosan akkor fa, ha összefüggő és körmentes. Az összefüggőség megköveteli, hogy bármely két pontja között vezessen út, a körmentességből pedig (A) szerint következik, hogy nem vezethet két út. Másrészt ha egy gráfban bármely két pont között pontosan egy út vezet, akkor nyilván összefüggő és kört sem tartalmazhat, hiszen a kör bármely két pontja között maga a kör két utat jelent.
TÉTEL:
(D) Osszűk egy összefüggő gráf pontjait tetszőlegesen két nem üres részre: legyen a két rész A és B. Ekkor biztosan van olyan él a gráfban, amely egy A-beli pontot köt össze egy B-beli ponttal.
(D’) Az állítás meg is fordítható: egy gráf pontosan akkor összefüggő, ha ez bármely két részre osztásánál teljesül.
6. feladat:
Bizonyítsuk be a fenti (D) és (D’) állítást!
A (D) ÁLLÍTÁS BIZONYÍTÁSA:
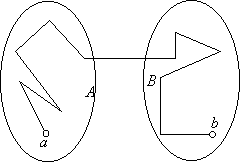
Legyen először a gráf összefüggő és bontsuk a gráf csúcsainak halmazát két nem üres részre: legyen a két rész A és B. Legyen a és b a két részhalmaz egy-egy csúcsa. Az összefüggőség miatt vezet közöttük út. Az út kezdőpontja és végpontja különböző részhalmazokban van, tehát van olyan él is, amelynek egyik végpontja az egyik halmazban van, másik végpontja a másikban. Ezt akartuk bizonyítani.
A (D’) ÁLLÍTÁS BIZONYÍTÁSA:
Ha van két nem üres ponthalmaz, A és B, amelyek között nem fut él, akkor a gráf nem lehet összefüggő, mert A semelyik pontjából nem vezet út B egyik pontjába sem. Ha viszont a gráf nem összefüggő, akkor van két pontja, amely között nem vezet út. Legyen ez a két pont a és b. Ekkor az a-ból úttal elérhető pontok halmaza és a komplementere sem üres (az előbbibe mindenképp beletartozik a, az utóbbiba b). E két halmaz között pedig nem vezet él.
TÉTEL:
(E) Egy n pontú fának pontosan n–1 éle van.
7. feladat:
Bizonyítsuk be az (E) állítást!
AZ (E) ÁLLÍTÁS BIZONYÍTÁSA
először egy eljárást definiálunk, amely a G fa egy G’ részgráfját választja ki:
I. ELJÁRÁS:
1. LÉPÉS:
Válasszűk ki a G gráf egy tetszőleges x1 pontját, ez a pont pontja lesz a G’ részgráfnak.
2. LÉPÉS:
Ha a gráfnak x1-en kívül nincs több pontja, befejezzük az eljárást.
Ha a gráfnak x1-en kívül is van pontja, akkor keressünk egy olyan x2 pontot, amely össze van kötve x1-gyel. Ilyen pontnak kell lennie, különben a gráf nem volna összefüggő. Az x2 pontot és az x1x2 élt beválasztjuk a G’ részgráfba.
k. LÉPÉS:
Tegyük fel, hogy az x1, x2, …, xk–1 pontokat már kiválasztottuk.
Ha az {x1, x2, …, xk–1}=A halmaz tartalmazza a G gráf összes pontját, akkor befejezzük az eljárást.
Ha az {x1, x2, …, xk–1}=A halmaz nem tartalmazza a G gráf összes pontját, akkor (D) szerint van olyan él, amely A és a gráf többi pontja között fut, vagyis egy A-beli xi pontot köt össze egy A-n kívüli xk ponttal. Az xk pontot és az xixk élt beválasztjuk a G’ részgráfba. (Az alábbi ábrán i=2 és k=8.)
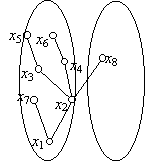
Ha G-nek n pontja van, akkor az eljárás pontosan az n-edik lépésben ér véget és az első lépés kivételével minden lépésben a G gráf egy új élét választja ki és veszi hozzá G’-höz. Ebből következik:
Az I. eljárással kapott G’ részgráf a G gráf összes pontját tartalmazza. Ha G-nek n pontja van, akkor G’-nek n–1 éle van.
DEFINÍCIÓ:
A G gráf olyan G’ részgráfjait, amelyek G összes pontját tartalmazzák, a gráf feszítő részgráfjának nevezzük.
8. feladat:
Bizonyítsuk be a következőket:
a) A G’ részgráf fa.
b) Ha egy összefüggő részgráfba behúzűnk egy élt, akkor az kört zár be.
c) Ha a G gráf, amelyből kiindultunk, fa, akkor G’ megegyezik G-vel.
MEGOLDÁS:
a): Az I. eljárás minden lépésben x1 egy szomszédját választja ki, vagy egy már kiválasztott szomszédjának szomszédját (x1 „másodszomszédját”), vagy x1 egy szomszédjának „másodszomszédját (x1 „harmadszomszédját”), stb. Vagyis minden lépésben olyan pontot választ ki, amelybe vezet út x1-bol. Tehát G’ teljesíti az összefüggőség második definícióját. Másrészt minden lépésben egy újonnan választott pontot kötünk össze egy már korábban kiválasztottal, ezért egyetlen beválasztott él sem zárhat be kört a már korábban beválasztott élekkel. A G’ részgráf tehát körmentes és összefüggő, tehát fa.
b): Egy összefüggő gráf bármely két pontja között megy út. Ha tehát két még össze nem kötött pontját összekötjük, akkor ez az él kört zár be az él két végpontját már eddig is összekötő úttal.
c) Ha a G gráf nem egyezik a G’ részgráfjával, akkor van olyan éle, amely nem szerepel G’-ben. De akkor b) szerint ez az él kört zár be a G gráfban. Tehát G nem lehet fa. Ha tehát G fa, akkor megegyezik a G’ részgráfjával.
(E) ÁLLÍTÁS BIZONYÍTÁSÁNAK befejezése:
Az (E) állítás bizonyítása most már azonnal következik a 8. feladat állításaiból: ha G n pontú fa, akkor valóban n–1 éle van, hiszen megegyezik azzal a G’ részgráffal, amelyet az I. eljárás kiválaszt. Márpedig G’-rol tudjuk, hogy n–1 éle van.
MEGJEGYZÉS:
Ha az I. eljárás alapján rajzoljuk fel a G fát, valahogy így fog kinézni:
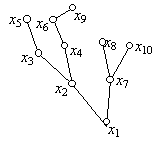
Ebből már látható, miért nevezik az ilyen gráfokat fának (bár a bokor talán megfelelőbb kép volna).
DEFINÍCIÓ:
Az x1 pontot a fa gyökerének szokás nevezni. (Természetesen a fa bármely pontja tekinthető gyökérnek!)
9. feladat:
Milyen G gráfokra működik változtatás nélkül az I. eljárás?
MEGOLDÁS:
Ha G összefüggő, akkor minden pontja elérhető a gyökérből induló úttal, tehát az I. eljárás a gráf minden pontját ki fogja választani. Vagyis minden összefüggő gráfra működik az eljárás. Ha G nem összefüggő, akkor az eljárás nem minden pontot ér el.
Ha G összefüggő, akkor G-nek egy olyan G’ részgráfját választja ki, amely G összes pontját tartalmazza, összefüggő és a pontszámnál eggyel kevesebb éle van (az első lépésben csak egy pontot választ ki, a további lépésekben minden ponttal együtt pontosan egy élet is kiválaszt), tehát fa.
DEFINÍCIÓ:
Ha az összefüggő G gráf egy G’ feszítő részgráfja fa, akkor G’-t G feszítő fájának, favázának vagy kaptafájának nevezzük.
Az I. eljárás ezek szerint tetszőleges összefüggő gráfnak megkeresi egy favázát. Ezzel beláttuk, hogy
TÉTEL:
(G) Tetszőleges összefüggő gráfnak van faváza.
TÉTEL:
(F) Egy n pontú összefüggő gráfnak legalább n–1 éle van.
c) ÖSSZEFÜGGŐ GRÁF FAVÁZAIRÓL:
A SZÉLESSÉGI FAVÁZ
A feszítő fát adó eljárásban két helyen van választási lehetőségünk: ott, hogy melyik xk-t választjuk és ott, hogy ha már kiválasztottuk, melyik korábban kiválasztott xi szomszédjával kötjük össze. Ennek megfelelően általában többféle feszítő fát tudunk kiválasztani és erre többféle eljárás ismert. Most ezek közül ismertetünk néhányat.
DEFINICIÓ:
Definiáljuk egy gráf pontjai közötti távolság fogalmát: Két pont távolságán a köztük a gráfban futó legrövidebb út hosszát értjük. (Ha a két pont között nem fut út a gráfban, akkor távolságukat értelmezhetjük végtelennek.)
Az alábbi ábrán például a b pont egyaránt kettő távolságra van az a, c, e pontoktól, a d ponttól viszont három távolságra van. Az a és e pont távolsága is három. Érdemes meggondolni, mely pontok távolsága változik, ha a gráfból elhagyjuk az fc élt.
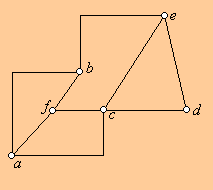
10. feladat:
Van-e olyan faváza minden összefüggő gráfnak, amely „megtartja” bármely két pont távolságát, azaz, ha a és b távolsága a gráfban d, akkor ugyanennyi a távolsága a favázban is?
MEGOLDÁS:
Egy kör bármely két szomszédos pontjának távolsága egy, viszont a favázában egy él nem fog szerepelni, ennek két végpontja közötti távolság tehát a favázban nagyobb lesz egynél. Nyilvánvaló, hogy ha az összefüggő gráf nem körmentes, akkor mindig lesz olyan éle, amely nem szerepel a favázban és ennek végpontjai között a favázban egynél nagyobb lesz a távolság.
Tehát ha egy összefüggő gráf nem körmentes (nem fa), akkor nincs a feladat feltételének megfelelő, azaz „távolságtartó” faváz, vagyis olyan faváz, amely a gráf bármely két pontja között megtartja a távolságot.
Most „enyhítünk” a feladat feltételén:
11. feladat:
Van-e olyan faváza minden összefüggő gráfnak, amely egy rögzített x ponttól vett összes távolságot „megtartja”?
MEGOLDÁS:
Tegyük fel először, hogy az I. eljárásban xk-t mindig úgy választjuk, hogy a lehető legkisebb indexű kiválasztott ponttal legyen összekötve. Másképp fogalmazva ez a következőt jelenti:
II. ELJÁRÁS:
1. LÉPÉS:
Kiválasztjuk x1-et, ez lesz a fa gyökere, és ezt tekintjük a fa első szintjének.
2. LÉPÉS:
Ha nincs több pontja a gráfnak, az eljárást befejezzük.
Ha van még pont a gráfban, akkor x1-nek vannak szomszédai, mert a gráf összefüggő. Kiválasztjuk x1 szomszédait – ez lesz az első szint. Behúzzuk a második szint pontjait a gyökérrel összekötő éleket.

3. LÉPÉS:
Ha a gráfnak már minden pontját kiválasztottuk, akkor az eljárást befejezzük.
Ha nem minden pontot választottunk még ki, akkor (D) állítás szerint a kiválasztott pontok és a még ki nem választott pontok között fut él, mert a gráf összefüggő.
Végigmegyünk az első szint pontjain, és mindegyiknek kiválasztjuk azokat a szomszédait, amelyek még nincsenek kiválasztva. Ezek alkotják a második szintet. A második szint a fent mondottak szerint nem üres. A második szinten azok a pontok vannak, amelyeknek van szomszédja az első szinten, minden második szintű pontot összekötünk egy első szintű szomszédjával (például azzal, „amelyik miatt” kiválasztottuk).
k. LÉPÉS:
Ha a gráfnak már minden pontját kiválasztottuk, akkor az eljárást befejezzük.
Ha nem minden pontot választottunk még ki, akkor (D) állítás szerint a kiválasztott pontok és a még ki nem választott pontok között fut él, mert a gráf összefüggő.
Általában a k+1-edik szintet azok a pontok alkotják, amelyek az k-adik szinten levő pontok szomszédai és még nem szerepelnek valamelyik korábbi szinten. A k+1-edik szint a fent mondottak szerint nem üres. Ezen a szinten azok a pontok vannak, amelyeknek van szomszédja az előző, k-adik szinten, minden k+1-edik szintű pontot összekötünk egy k-adik szintű szomszédjával (például azzal, „amelyik miatt” kiválasztottuk).
Az eljárás akkor ér véget, amikor a gráf minden pontját besoroltuk valamelyik emeletre.
DEFINÍCIÓ:
Az így kapott feszítő fát szélességi faváznak nevezzük.
A távolság és a szélességi faváz definíciójából következik, hogy
a szélességi faváz i-edik szintjén pontosan azok a pontok vannak, amelyek x1-tol i távolságra vannak.
11.a feladat:
Ha egy adott összefüggő gráfban kijelölünk egy y pontot, egyértelműen meghatározott-e az y ponthoz tartozó, vagyis az y gyökerű szélességi faváz?
MEGOLDÁS: Az adott ponthoz tartozó szélességi faváz nem feltétlenül egyértelmű: a
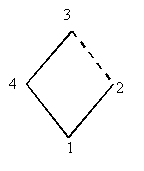
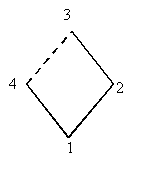
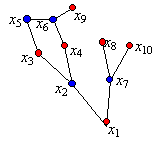
szintek egyértelműek, de az élek nem: hogy melyik élek fognak szerepelni a favázban, ez függ attól, hogy a soron levő pont még nem szereplő szomszédait milyen sorrendben írjuk be a favázba. Ha például veszünk egy négy hosszú kört, amelynek pontjai sorban 1, 2, 3, 4, akkor az 1-es ponthoz tartozó szélességi faváz első szintjén a 2-es és a 4-es pont fog szerepelni, a második szintjén a 3-as. De attól függően, hogy a 2-es és 4-es pontot ilyen sorrendben vettük be a gráfba, vagy fordítva, a 3-as pont a 2-es, illetve a 4-es ponthoz is csatlakozhat a szélességi favázban. (A két ábra mutatja a két lehetőséget, a szaggatottan behúzott él éle a gráfnak, de nem éle a faváznak.)
Szükségünk lesz néhány fával kapcsolatos definícióra:
DEFINÍCIÓ:
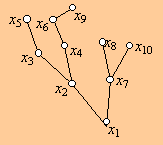
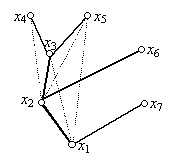
Egy fában az x pont apjának nevezzük azt a pontot, amellyel az alacsonyabb szintű pontok közül össze van kötve. Ez a pont nyilván egyértelműen meg van határozva (egyetlen ilyen pont van és az az i–1-edik szinten van). Az x pont fiának nevezzük az összes olyan i+1-edik szintű pontot, amellyel a fában (!) össze van kötve. Vagyis amelyiknek ő az apja. Egy pont utódai fiai, fiainak fiai, stb., tehát minden olyan magasabb szintű pont, amellyel út köti össze; elődei az apja, az apjának az apja, stb., tehát azok a pontok, amelyek a pontból a gyökérhez vezető úton vannak (így maga a gyökér is). Két pont összehasonlítható pontja a fának, ha az egyik elődje a másiknak (és a másik utódja az egyiknek).
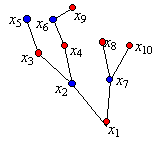
Az alábbi ábrán például az x2 pont apja x1, a gyökér, ez minden más pontnak is elődje, az x2 pont fiai az x3 és x4 pontok, további utódai x5, x6 és x9. Ez utóbbinak nincs utódja, apja viszont az x6 pont.
12. feladat:
Adott egy összefüggő gráf, G. Szeretnénk olyan favázat keresni, amelyre igaz a következő: ha e=xy éle G-nek, akkor x és y a faváznak vagy azonos, vagy szomszédos szintjén van. Vagyis a gráf minden éle a favázon azonos vagy szomszédos szintek között fut. Milyen G gráfokra van ilyen faváz?
MEGOLDÁS:
Bármely ponthoz tartozó bármely szélességi faváz megfelel. Ez következik a szélességi faváz definíciójából. Tegyük fel ugyanis, hogy az xy él alacsonyabb szintű végpontja – legyen ez x – az i-edik szinten van és tegyük fel, hogy y magasabb szintre került. De ekkor biztosan felkerült az i+1-edik szintre, hiszen erre a szintre az összes olyan pontot feltesszük, amely (legalább) egy i-edik szintű ponttal össze van kötve.
d) KITÉRO:
A SZÉLESSÉGI FAVÁZ KERESÉSÉNEK (= II. ELJÁRÁS) SZÁMÍTÓGÉPES MEGVALÓSÍTÁSÁRÓL
A II. eljárásban adott algoritmus végrehajtásához szükségünk van annak adminisztrálására, hogy melyek azok a pontok, amelyekkel már végeztünk, (amelyeknek már összes szomszédját megkerestük), és melyek a „vizsgálat alatt levo” pontok, azaz azok, amelyek már sorra kerültek mint szomszédok (mint fiúk), de még nem kerestük meg a szomszédaikat (a fiaikat). Az előbbi egyszerűen megoldható, amennyiben minden pontot megindexelünk. Kezdetben minden index 0, és ha egy pontot vizsgálat alá veszünk, indexét –1-re változtatjuk, ha pedig végeztünk vele, indexét 1-re változtatjuk. Nem 0 indexű pontokat nem veszünk hozzá újra a favázhoz, sem a “vizsgálat alatt levo” pontokhoz. Viszont a –1 indexű pontokat külön tárolni célszerű, mégpedig úgy, hogy mindig hozzáférjünk a legrégebben tárolt ponthoz, és azt könnyen el tudjuk hagyni, ha már végeztünk vele.
Nyilvánvaló, hogy ha a II. eljárást megvalósító, most leírt algoritmus egy nem 0 indexű ponthoz ér, akkor a gráfban kört talált. A gráf pontosan akkor körmentes, ha ez az algoritmus sosem ér újra nem 0 indexű ponthoz.
Ha kipróbáljuk konkrét gráfokon, akkor jól látható, hogy a II. eljárás alapos, körültekinto, „megfontolva haladó” algoritmus: a kiinduló pont „környezetét” járja végig táguló körökben.
Megjegyezzük, hogy a szélességi faváz „polinomiális időben” megtalálható, ami azt jelenti, hogy van olyan p(n) polinom, hogy bármely n pontú gráf szélességi favázának megtalálásához elég p(n) idő.
A szélességi faváz a pontok távolságával kapcsolatban merült fel. Most még pár oldalról megvizsgáljuk a gráfban definiált távolságfogalmat.
e) A GRÁFBELI TÁVOLSÁGFOGALOMRÓL,
A GRÁF ÁTMÉROJE
13. feladat:
Igaz-e, hogy a gráfokban definiált távolságfogalom „valódi távolságfogalom” abban az értelemben, hogy teljesíti a háromszög-egyenlőtlenséget? Vagyis ha a gráfnak vesszük három pontját, a-t, b-t és c-t, akkor az a és b pontok távolsága és a b és c pontok távolsága együtt nem kisebb az a és c pontok távolságánál: d(a, b) + d(b,c) ³ d(a,c) ?
MEGOLDÁS:
Igaz, ez következik (B)-bol.
Fontos kérdés, hogy egy gráf mennyire „tömör”, vagy másképp fogalmazva: megkérdezhetjük, hogy két pont maximálisan milyen távol van egymástól a gráfban. Véges ponthalmazoknál a pontok között fellépő maximális távolságot nevezzük a ponthalmaz átmérőjének. Pontosan ugyanígy bevezethetjük egy gráf átmérőjének a fogalmát is:
DEFINÍCIÓ:
Egy véges gráf átmérőjének a gráf pontjai között fellépő legnagyobb távolságot nevezzük.
Ha a gráf nem összefüggő, akkor mondhatjuk, hogy az átmérő végtelen, vagy megszoríthatjuk a definíciót összefüggő gráfokra.
Megjegyezzük, hogy a definíció kiterjeszthető irányított gráfokra és végtelen gráfokra is. Utóbbi esetben azonban hozzá kell tenni, hogy ha nincs legnagyobb távolság, akkor a gráf átmérője végtelen: ez az eset például egy végtelen hosszú útnál. Végtelen gráfoknál tehát előfordulhat, hogy a gráf összefüggő, de az átmérő végtelen.
Az átmérőre vonatkozó egyszerű feladatok a következők:
14. feladat:
a) Mely gráfoknak 1 az átmérője?
b) Mennyi a csillag átmérője?
c) Mennyi az 5 hosszú kör átmérője? És a 7 hosszúé? Mennyi általában az n pontú köré?
d) Mennyi egy 10 élből álló út átmérője? És általában az n élu úté?
e) Mennyi a tetraédek és a kocka élgráfjának átmérője?
f) Mennyi az oktaéder élgráfjának átmérője?
g) Mennyi az ikozaéder élgráfjának átmérője?
h) Egy fának a gyökéren kívül 5 emelete van. Legfeljebb mekkora lehet az átmérője?
MEGOLDÁS:
a) A teljes gráf átmérője nyilván 1 és 1 gráf átmérője nyilván pontosan akkor 1, ha a gráf teljes gráf.
b) A csillagban a gyökértől minden pont 1 távolságra van, viszont bármely két másik pont 2 távolságra van. Tehát ha a csillagnak legalább 3 pontja van, akkor átmérője 2. A 2 pontú csillag átmérője 1.
c) Az 5 hosszú kör átmérője 2(!), mert bármely két nem-szomszédos pontját egy 2 és egy 3 élu út köti össze:
Ugyanígy a 7 hosszú kör átmérője 3 és általában a 2k+1 hosszú köré k. A 2k hosszú köré szintén k (a négy hosszúé ketto, a hat hosszúé három, stb.).
d) Egy út átmérője nyilván a két végpontjának távolsága, vagyis egy út átmérője megegyezik az út hosszával.
e) A tetraédek élgráfja 4 pontú teljes gráf, és a teljes gráfok átmérője a) szerint 1. A kocka élgráfjának az átmérője 3: két szemközti csúcs távolsága ugyanis ennyi. Bármely két, nem szemközti csúcs távolsága ennél kevesebb: 1 vagy 2.
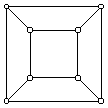
f) Az oktaéder élgráfjában minden pont pontosan egy másikkal, a szemköztivel nincsen összekötve. Ettől tehát kettő távolságra van. Az oktaéder élgráfjának átmérője ezek szerint 2.
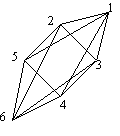
g) Az ikozaéder élgráfjában minden pontnak 5 szomszédja van, ezek mindegyike további két ponttal van összekötve, de összesen öttel, tehát minden pontnak 5 másodszomszédja van. Marad egy pont, ami ben is minden ponttal van egy szemközti pont, ez 3 távolságra van tole, így az ikozaéder élgráfjának átmérője 3. (Az ábrán a legbelső pont körüli ötszög pontjai az első szomszédok, a külső ötszög pontjai a másodszomszédok, a szemközti csúcsot, amely a külső ötszög pontjaival van összekötve, az ábrán nem tüntettük fel: ez van a legbelső ponttól 3 távolságra.)
h) Ha egy fának 5 emelete van a gyökéren kívül, akkor bármely pontjából 5 élu úttal elérhető a gyökér, s így bármely két pontja között legfeljebb 10 élu út megy, tehát az átmérő legfeljebb 10. A 10 élu (11 pontú) út a példa rá, hogy van olyan fa, amelyben pontosan 10 az átmérő és 5 emelet van.
Már sokkal bonyolultabb az a kérdés, hogy milyenek a 2-átmérőjű gráfok. Erre a kérdésre a 29. és a 49. feladatban térünk vissza, majd a IV. fejezet 18–20. feladataiban foglalkozunk részletesen egy nevezetes 2-átmérőjű gráffal.
Az átmérővel kapcsolatban egyelőre csak annyit jegyzünk meg, amit az előző algoritmusainkból ki tudunk róluk olvasni:
14.x feladat:
Bizonyítsuk be, hogy összefüggő gráf átmérője is polinomiális időben meghatározható.
BIZONYÍTÁS:
A bizonyításhoz az egyszerűség kedvéért bevezetjük egy gyökeres fa magasságának fogalmát: ez a gyökértől legtávolibb pont távolsága a gyökértől. Vagy másképp: a fa (gyökértől különböző) szintjeinek száma.
Minden x ponthoz megkeressük az x gyökerű szélességi favázat. Ennek magassága az x-tol legtávolabbi pont távolsága. Jelöljük ezt t(x)-szel. Ha minden x-re meghatározzuk t(x)-et, akkor a gráf átmérője a legnagyobb t(x) lesz. Márpedig t(x) meghatározásához elég p(n) idő, és n pont van, ezért az összes t(x) meghatározásához is elég np(n) idő, ami szintén polinom. A maximum meghatározása minden x-nél csak plusz egy lépés: összehasonlítjuk azt, amit az aktuális t(x)-re kaptunk, az eddigi legnagyobb értékkel és a kettő közül a nagyobbat tároljuk.
f) ÖSSZEFÜGGŐ GRÁFOK FAVÁZAI (folytatás):
MÉLYSÉGI FAVÁZ
15. feladat:
Van-e olyan faváza minden összefüggő gráfnak, amelyben minden él egy elődöt és egy utódot (tehát két, a favázban összehasonlítható pontot) köt össze?
MEGOLDÁS:
Egyáltalán nem magátólértetődo, hogy ilyen faváz mindig létezik. Persze, ha a gráf fa, akkor megfelel. Ha a gráf teljes, akkor bármely olyan út megfelel, amely a gráf minden pontját tartalmazza (az ilyen utat, ha van, a gráf Hamilton-útjának nevezzük). Érdemes ezt összevetni azzal, hogy milyen favázat ad a körkörösen haladó keresés ugyanennél a gráfnál. Itt egy csillagot kapunk, ami már sejtetni engedi, hogy mikor kaphatunk a második kérdés feltételét kielégítő favázat. Nyilvánvaló az is, hogy ha a gráfnak van Hamilton-útja, akkor ez az út megfelelő faváz. Általában is nyilvánvaló, hogy ha a gráfnak van Hamilton-útja, akkor bármely Hamilton-út megfelel a célunknak, ha egyik végpontja a gyökér. Hiszen egy ilyen Hamilton-útban bármely két pont közül az egyik a másik utódja. Vizsgáljuk meg még azt a gráfot, amelyben három háromszög illeszkedik egy pontban:
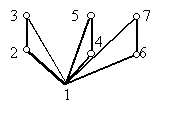
Ha az 1-es pontot választjűk gyökérnek, akkor a szélességi faváz egy csillag lesz, s ez nyilván nem felel meg, hiszen a kimaradó élek mindegyike azonos szintű, tehát nem összehasonlítható pontok között fut. Nézzük, mi lehet jó. Nyilvánvaló, hogy például a 2-es és 3-as pont közül egyik az első emeletre, közvetlenül a gyökér fölé fog kerülni, feltehetjük, hogy a 2-es kerül az első emeletre. De akkor a 3-as pontnak a második emeletre kell kerülnie, különben az első emeletre kerülne, s akkor a 23 él nem előd és utód között futna. Hasonlóan a 4-es és 5-ös pont közül is az egyik az első emeletre kerül, a másik a másodikra, és a 6-os és 7-es pontra is ugyanez áll. A faváz most így néz ki:
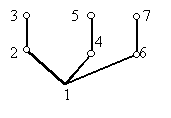
Általában is világos, hogy ha a keresés során eljutunk egy xyz… út xy éléhez, tehát sorra került x és utána bevettük az xy élt is a fába, akkor z-t y utódjaként kell a fához illesztenünk. A legegyszerűbb az, ha y szomszédjaként vesszük sorra. Vagyis itt a szélességi („körkörös”) kereséssel ellentétben célszerű mindig „előre törni”. Olyan algoritmussal érdemes tehát próbálkoznunk, amelyik mindig előre megy, amíg ez lehetséges. Ha valahol elakadunk, akkor visszakozunk, de akkor is csak a lehető legkevesebbet, és onnan próbálunk meg előre törni új pontok felé. Ez lesz a mélységi keresés. Ha egy pontot elérünk, nem az összes szomszédja érdekel minket, hanem csak egy.
A III. ELJÁRÁS tehát a következő: Ha elérünk egy y ponthoz, keresünk egy olyan szomszédját, amelyet még egyetlen korábbi lépésben sem értünk el, ha van ilyen, ezt is felvesszük az elért pontok közé az y-ból hozzá vezető éllel együtt, és ez lesz az új y, majd ettől a ponttól folytatjuk a keresést. Akkor akadunk meg, ha olyan y ponthoz érünk, amelynek már minden szomszédját korábban elértük. Ekkor visszamegyünk ahhoz a ponthoz, ahonnan y-t elértük, és onnan próbálkozunk: ez (vagyis y fabeli „apja”) lesz az új y.
Az algoritmust ezzel megadtuk. Megadjuk valamivel formálisabban is:
1. LÉPÉS:
Kiválasztunk egy x1 pontot, ez lesz a fa gyökere. Legyen y=x1. (y változik az eljárás során!)
2. LÉPÉS:
Keressük meg y-nak egy szomszédját. Ha ilyen pont nincs, akkor az eljárást befejezzük (ekkor a gráf egy pontból állt).
Ha y-nak van szomszédja, válasszűk ki egy szomszédját, legyen ez x2, a faváznak éle lesz az yx2= x1x2 él és most y=x2.
k. LÉPÉS:
Tegyük fel, hogy már kiválasztottuk az x1,x2,…,xk–1 pontokat és y=xi. Járjuk végig y szomszédait, amíg nem találunk olyat, ami még nem szerepel a kiválasztott xj-k között.
1. eset: Ha y-nak van ilyen szomszédja (amely tehát még nem szerepel a kiválasztott xj-k között), akkor az előszörre talált ilyen pont lesz xk, a favázba beillesztjük az yxk=xixk éllel együtt és y=xk.
2. eset: Ha y-nak minden szomszédja szerepel a kiválasztott xj pontok között, akkor megkeressük y apját az xj pontok között, ez lesz az új y, s erre ismételjük az eljárást. Egyetlen esetben nincs y-nak apja: ha y a gyökér. Az eljárás tehát akkor ér véget, ha visszaérünk a gyökérhez, és a gyökérnek már minden szomszédja szerepel a fában. Ekkor az eljárást befejezzük.
Az alábbi hatpontú gráfban a vastagon jelölt éleket a következő sorrendben húztuk be: x1x2, most y=x2. A következő lépésben behúztuk az x2x3 élt és y=x3, ezután behúztuk az x3x4 élt és y=x4. Eddig „nyílegyenesen” haladtunk előre. A következő lépésben azonban y=x4-bol csak visszafelé megy él (x4x2, ezt nem választjuk ki, az ábrán szaggatott), tehát y=x3 és nem húzűnk be élt. Az x3x1 él visszafelé megy, ezt nem húzzuk be (az ábrán szaggatott), viszont behúzzuk az x3x5 élt és y=x5. Innen megint nem megy „előre” él csak visszafelé az x5x2 és x5x1 él (az ábrán szaggatott), ezért visszamegyünk x5 apjához: y=x3, innen sem tudunk már előbbre lépni, ezért y=x2. Behúzhatjuk az x2x6 élt és y=x6, innen már nem tudunk előrébb lépni, tehát ismét y=x2 lesz, onnan sem mehetünk előrébb, tehát y=x1. Most behúzzuk az x1x7 élt és y=x7. Innen nem mehetünk előrébb, tehát ismét y=x1 lesz, s onnan sem indul már új él, tehát az eljárásnak vége. A kiválasztott faélek vastagítva vannak, a többi él szaggatott.
DEFINÍCIÓ:
Ezt az eljárást mélységi keresésnek nevezik.
Az eljárást ezzel megadtuk. A kérdés csak az, hogy a) valóban azt kapjuk, amit várunk tole: egy olyan favázat, amelybe a gráf összes éleit behúzva mindig elődöt és utódot fogunk összekötni; b) elég gyors-e ez az eljárás; és c) hogyan valósítható meg ez az eljárás számítógépen?
először vizsgáljuk meg az a) és b) kérdést. Mindkét kérdésre igenlő a válasz, de egyik válasz sem magától értetődo. Ez az algoritmus is mohó, csakúgy, mint a szélességi keresés: mindkettő minden pillanatban a legkézenfekvőbbet teszi – csak mást tekint legkézenfekvőbbnek. A szélességi inkább védekező jellegű algoritmus, a mélységi inkább offenzív algoritmus. Mindkét esetben meg kell tehát vizsgálnunk, hogy ami adott pillanatban a legkézenfekvőbb, az végeredményben is a legjobb-e, vagy egyáltalán célhoz vezet-e.
Be kell tehát bizonyítanunk, hogy az ismertetett algoritmus véget ér, összefüggő gráf esetén valóban favázat ad és a kapott faváznak megvan a feladatban kívánt tulajdonsága. Ez azonban következik abból, hogy
TÉTEL:
a mélységi keresés – csakúgy, mint a szélességi keresés – az összefüggő gráf összes pontjához eljut és minden élét bejárja.
15.a feladat:
Bizonyítsuk be ezt az állítást!
Ahogy a szélességi keresésre (II. eljárás), úgy a mélységi keresésre (III. eljárás) is igaz, hogy ha eljut egy ponthoz, akkor annak összes szomszédjához is eljut. Hiszen a gyökérhez csak akkor jut vissza, ha már minden pontból kimerítette az összes továbblépési lehetőségeket, tehát minden pont minden szomszédját bejárta. Vagyis az eljárás által bejárt pontok halmazából nem vezet ki él. Minthogy a gráf összefüggő, ebből már (D) szerint következik, hogy a gráf minden pontja sorra került. Ebből viszont a dőlt betűs állítás szerint következik, hogy minden élt is bejárt.
MEGJEGYZÉS:
Az is igaz, hogy minden élt pontosan kétszer jár be: mindkét végpontjánál egyszer „találkozik” az éllel.
Az ismertett eljárásoknak az a tulajdonsága, hogy az összefüggő gráf minden pontját és élét bejárják, sok más, bonyolultabb algoritmusnál is szükségessé teszi oket!
Bizonyítsuk be, hogy a mélységi keresés (III. eljárás) az összefüggő gráfnak valóban egy favázát adja meg!
A mélységi keresés – ismét a szélességi kereséshez hasonlóan – nem választ be olyan élt a felépítendő favázba, amely két korábban már beválasztott pontot köt össze, tehát nem hoz létre kört. De minden élt sorra vesz, így összefüggő gráf esetén valóban feszítő fát fog adni.
DEFINÍCIÓ:
A III. eljárással kapott faváz az összefüggő gráf mélységi faváza.
15.c feladat (a 15. feladat megoldásának befejezése):
Végül bizonyítsuk be, hogy a mélységi faváz valóban rendelkezik a 15. feladatban megkövetelt tulajdonsággal.
A 15. feladat megoldásának befejezése:
Nyilvánvaló, hogy a mélységi kereséssel kapott faváznak megvan a második kérdésben követelt tulajdonsága. Legyen ugyanis uv a gráf egy éle. Feltehetjük, hogy a keresés során u és v közül először u került sorra. Amikor elértünk u-hoz, akkor minden ezután beválasztott pont u utódja lesz a fán, amíg csak u-ból „vissza nem lépünk”. De vissza csak akkor lépünk, ha már u minden szomszédja szerepel, tehát eddigre a v pont sorra kerül. Tehát: a v pont u után és az u-ról való visszalépés előtt kerül sorra, de ez azt jelenti, hogy v biztosan u utódja lesz a fán.
g) ÖSSZEFÜGGŐ KOMPONENSEK
A favázak, illetve a fenti kereső algoritmusok további fontos tudnivalókat is szolgáltatnak a gráfról:
1) Ha a keresés során egy már szereplő ponthoz jutnak vissza mint új szomszédhoz, ez pontosan azt jelenti, hogy a gráfban találtak egy kört.
2) Felmerül a kérdés, hogy mi történik, ha eljárásunkat egy nem összefüggő gráfra alkalmazzuk. A 15.a feladat megoldásánál láttuk, hogy az eljárásban sorra kerülő pontok együtt a gráf ponthalmazának egy olyan H részhalmazát adják, amelyből a) nem vezet ki él a sorra nem vett pontokhoz, b) a gyökérből H minden pontjába vezet út, tehát a H részhalmaz összefüggő részgráfot feszít a gráfban. E két tulajdonságot együtt úgy lehet összefoglalni, hogy H a gráf ponthalmazának egy tartalmazásra nézve maximális olyan részhalmaza, amely összefüggő részgráfot feszít. Röviden ezt úgy is szoktűk mondani, hogy H maximális összefüggő részhalmaza a gráfnak, vagy másképpen: H a gráf egy összefüggő komponense:
DEFINÍCIÓ:
A G gráf pontjainak tartalmazásra maximális összefüggő részhalmazait a gráf összefüggő komponenseinek nevezzük.
16. feladat:
Bizonyítsuk be, hogy ha H és H’ a gráf két összefüggő komponense, akkor vagy megegyeznek, vagy diszjunktak.
Vagyis:
TÉTEL:
Egy tetszőleges gráf felbontható összefüggő komponensek diszjunkt uniójára. A felbontás egyértelmű. Így minden pont pontosan egy összefüggő komponensben van benne, ezt nevezzük a pont komponensének. Két pont pontosan akkor tartozik ugyanabba a komponensbe, ha vezet közöttük út. Egy gráf pontosan akkor összefüggő, ha egyetlen összefüggő komponensből áll.
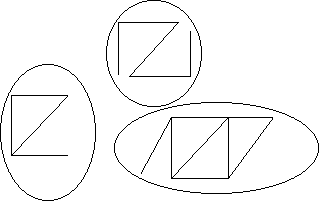
A fenti gráf például három komponensből áll, egy négy-, egy öt- és egy hatpontúból.
BIZONYÍTÁS:
Legyen tehát H és H’ két maximális összefüggő részhalmaz. Ha diszjunktak, kész vagyunk. Ha van közös pontjuk, akkor ebből a közös pontból mind H, mind H’ minden pontja elérhető úttal, tehát H és H’ egyesítésének minden pontja is elérhető belőle úttal, vagyis egyesítésük is összefüggő részhalmaz (összefüggő részgráfot feszít). De H és H’ tartalmazásra maximális összefüggő részhalmazok voltak, s ez csak úgy lehet, ha H=H’.
A feladat többi állítása nyilvánvaló következménye a feladat most bizonyított első állításának.
Ha a három (I., II., III.) eljárás közül bármelyiket tetszőleges gráfra futtatjuk, akkor bármely pontnak megtalálja az összefüggő komponensét. Ha pedig egy összefüggő komponenst megtalált, akkor ezt elhagyhatjuk a gráfból, s megismételhetjük az eljárást. Így pontosan annyi komponense van a gráfnak, ahányszor „újraindítjuk” az eljárást.
Mindhárom algoritmus alkalmas tehát arra is, hogy eldöntse adott gráfról, hogy összefüggő-e. A gráf pontosan akkor összefüggő, ha nem kell újraindítani az eljárást.
Az eljárások általános esetben egy feszítő erdőt adnak, amely a gráf minden komponensében egy-egy favázat ad meg.
h) KITÉRŐ:
A MÉLYSÉGI KERESÉS SZÁMÍTÓGÉPES MEGVALÓSÍTÁSA
A III. eljáráshoz célszerű a gráfot láncolt szomszédsági listán tárolni. Ez kissé egyszerűsítve azt jelenti, hogy minden ponthoz van egy lista, amely valamilyen sorrendben tartalmazza e pont szomszédait, és ezek a listák össze vannak kötve. A mélységi keresés elindul egy ponttól, megkeresi annak első szomszédját a szomszédsági listán, behúzza a favázba az összekötő élt, majd tovább halad az újonnan talált pont szomszédsági listájának legelső (még fel nem keresett) pontjához. Így halad előre nyíl egyenesen, és csak akkor fordul vissza, ha egy olyan ponthoz ér, amelynek szomszédsági listáján szereplő minden pontot már korábban felkeresett (a felkeresés tényét itt is lehet egy 1-es indexszel adminisztrálni). A már felkeresett pontokat itt egy olyan adatstruktúrában kell tárolni, ahol az utoljára felkeresett ponthoz tudunk hozzáférni (ilyen a verem).
Végül az eljárás leírásából és a megvalósítás leírásából kiolvasható, hogy a mélységi keresés is megvalósítható polinomiális időben, azaz van olyan p(n) polinom, hogy az eljárás minden összefüggő n pontú gráfnak p(n) idő alatt megtalálja a mélységi fáját (illetve minden n pontú egyszerű gráfnak p(n) idő alatt megadja egy mélységi erdővázát).
17. feladat:
Bizonyítsuk be, hogy egy gráf leghosszabb útja is megtalálható polinomiális időben.
BIZONYÍTÁS:
Ha a mélységi keresést az x pontból indítjuk, akkor a legmagasabb szintű pontokba futó utak az x pontból induló leghosszabb utak, ez következik abból, hogy a gráf minden pontja a faváz egy elődje és utódja között fut (lásd az előző feladatot). Egy ilyen út megtalálásához elegendő tehát (lényegében) p(n) lépés. Ha minden pontra megcsináljuk ezt, akkor legfeljebb np(n) lépésben megkapjuk minden pontból a leghosszabb utat, s ezek közül a leghosszabb(ak) lesz(nek) a gráf leghosszabb útja(i).
i) FAVÁZ FELHASZNÁLÁSA PÁROS GRÁFOK JELLEMZÉSÉRE
Akár a szélességi faváz, akár a mélységi faváz (valójában bármely faváz) segítségével bebizonyítható egy fontos, a páros gráfokra vonatkozó tétel.
Mint emlékezetes, páros gráfnak az olyan gráfokat nevezzük, amelyeknek csúcsai két osztályba sorolhatók úgy, hogy a gráf minden éle különböző osztályba tartozó csúcsokat köt össze:
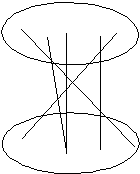
Minden fa páros gráf: a gyökeret rakjuk az első osztályba, az első szint pontjait a másodikba, majd általában a páros szintek pontjai kerülnek az első osztályba, a páratlan szinteké a másodikba. Ekkor nyilván nem fut él a két osztály között. Az ábrán pirossal és kékkel jelöltük a két szint pontjait. Általában is elmondhatjuk, hogy egy gráf pontosan akkor páros, ha csúcsai két színnel színezhetők úgy, hogy azonos színű pontok között ne fusson él.
Nyilvánvaló az is, hogy
TÉTEL:
egy páros gráfban minden kör (ha van) páros hosszúságú,
azaz:
páros gráfban nincs páratlan hosszúságú kör,
hiszen a kör szomszédos pontjai mindig ellentétes osztályhoz tartoznak, s ez páratlan kör esetén ellentmondáshoz vezet. De vajon igaz-e ennek az állításnak a megfordítása is:
18. feladat:
Igaz-e, hogy ha egy gráfban minden kör hossza páros, akkor a gráf páros gráf?
MEGOLDÁS:
Nyilván elég az állítást összefüggő gráfokra vizsgálni, hiszen egy gráf pontosan akkor páros gráf, ha minden összefüggő komponense páros gráf. Legyen tehát G egy összefüggő gráf, amelyben minden kör hossza páros. Keressük meg egy feszítő fáját, például egy szélességi favázát. Színezzük ezt ki két színnel úgy, hogy a páros szintek pontjai (és a gyökér) pirosak legyenek, a páratlan szintek pontjai kékek. Ha sikerül a gráf pontjait két osztályba sorolni úgy, hogy csak különböző osztályok között menjen él, ez csak úgy lehetséges, ha a kék pontok alkotják az egyik osztályt, a pirosak a másikat. Ám a szélességi faváz bizonyított tulajdonsága szerint a gráf minden éle vagy azonos szintű pontok között fut, vagy szomszédos szintek között. A szomszédos szintek között futó élek „nem zavarnak”, mert különböző színű pontokat kötnek össze. Ha van olyan e=xy él, amely két azonos szintű pontot köt össze, akkor keressük meg x és y első közös osét, legyen ez u. Az x-bol u-ba vezető út és az y-ból u-ba vezető út egyforma hosszú és u-n kívül nincs közös pontjuk, hiszen u az első közös os. Ha a két utat összeillesztjük és az így kapott páros hosszú úthoz hozzávesszük az e élt, akkor egy páratlan kört kapunk. Ha ilyen él nincs, akkor viszont a fekete és a fehér pontok valóban két megfelelő osztályra bontják a gráf pontjait. (Az ábrán u=x5, v=x6, a közös os x2, a talált páratlan kör x5x3x2x4x6x5.)
MEGJEGYZÉS:
Az ismertetett algoritmus több szempontból is nagyon kedvezo. Egyrészt végrehajtható polinomiális időben. Másrészt eredményeképpen vagy megkapjuk a gráf egy „jó színezését két színnel”, vagy kapunk egy páratlan kört, vagyis az algoritmus mindenképpen pozitív eredményt ad, akkor is, ha nem páros a gráf: megmutatja ennek az okát. (Nem minden kereső feladatnál van ez így, például ha Hamilton-kört keresünk – tehát olyan kört, amely a gráf minden pontján átmegy –, arra nem ismeretes olyan tulajdonság, amely ebben az értelemben „oka” lehetne annak, hogy nincs Hamilton-köre a gráfnak. Tehát minden Hamilton-kereső algoritmus vagy mutat egy Hamilton-kört, vagy azt mondja: nincs ilyen, és kénytelen vagyunk elhinni, nem tudjuk ellenőrizni – legalábbis ilyen hatékonyan nem.)
Érdemes összefoglalni a kapott állításokat:
TÉTEL:
Egy gráf pontosan akkor páros gráf (vagyis akkor oszthatók pontjai két osztályba úgy, hogy osztályon belül ne fusson él), ha minden köre páros.
j) ERDŐ ÉLSZÁMA,
ÚJ ELJÁRÁS FA- ÉS ERDŐVÁZ KERESÉSÉRE
Korábban ígértünk egy másik bizonyítást a 2. feladatra, tehát arra, hogy bármely n pontú körmentes gráfban legfeljebb n–1 él van. Összefüggő körmentes gráfokra, azaz fákra már (E)-ben bebizonyítottuk, hogy pontosan ennyi éle van. Most egy új bizonyítást adunk az általános esetre, ami egyben pontosítja is 2. feladat állítását:
Ha a gráf nem összefüggő, akkor vegyük az összefüggő komponenseit, vagyis a legnagyobb összefüggő részgráfjait. Körmentes gráf minden részgráfja is körmentes. Így minden összefüggő komponense is körmentes, azaz fa. Ezért a körmentes gráfokat szokás erdőnek, vagy ligetnek is nevezni. (E) szerint egy ilyen erdő minden összefüggő részgráfjának a csúcsszámnál eggyel kevesebb éle van. Ebből kapjuk a következő tételt:
TÉTEL:
Egy körmentes gráf (azaz erdő vagy liget) élszáma egyenlő a csúcsok száma – az összefüggő komponensek száma.
(G)-ben láttuk, hogy minden összefüggő gráfnak van feszítő fája, így egy tetszőleges gráf minden összefüggő komponensének is van. Ebből viszont következik, hogy
(H) Ha egy gráfnak c darab komponense van, akkor van c fából álló feszítő erdeje. Ezért minden n pontú, c komponensből álló gráfnak legalább n – c éle van.
Abból a tényből, hogy összefüggő gráfnak van faváza, következett az (F) állítás, amely szerint összefüggő n pontú gráfnak legalább n–1 éle van. Az összefüggő komponens fogalmát használva erre is adhatunk egy új bizonyítást:
Hagyjuk el a gráf összes élét. Az így kapott üres gráf n komponensből áll. Most húzzuk be újra egyesével a gráf éleit. Nyilvánvaló, hogy minden él behúzása vagy eggyel csökkenti a komponensek számát (ha az él két különböző komponenst köt össze), vagy változatlanul hagyja (ha azonos komponenshez tartozó csúcsokat köt össze). Az eljárást addig folytatjuk, amíg a gráf összes élét be nem húzzuk. Végeredményben összefüggő gráfot kell kapnunk, vagyis olyan gráfot, amelyben a komponensek száma egy. Minden él behúzásánál maximum eggyel csökkent a komponensek száma és kezdetben n volt, ezért legalább n–1 élt kellett behúznunk.
MEGJEGYZÉS:
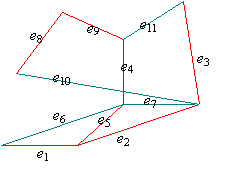
A bizonyításban ismertetett eljáráson csak kicsit kell változtatni ahhoz, hogy ez is a gráf egy favázát keresse meg, vagy általában is egy új algoritmust kapjunk összefüggő gráf feszítő fájának megkeresésére. Mindössze azt kell mondanunk, hogy ha egy él két eddig különböző komponens között fut, vagyis két komponenst egyesít, akkor kiválasztjuk a feszítő fába, ha azonos komponens pontjai között fut, akkor nem választjuk ki (hanem „szemétbe dobjuk”). Az ábrán zölddel jelöltük az elhagyott éleket, pirossal a kiválasztottakat. Az e1, e2, e3 élek egy hárompontú komponenst hoznak létre, e4 egy másik kétpontút. Az e5 él ezeket egyesíti, az e6 és e7 a kapott ötpontú komponensen belül fut, e8 egy új, kétpontú komponenst hoz létre, e9 ezt egyesíti az ötpontúval, végül e10 és e11 már „felesleges”, hiszen a piros élek már egy komponenssé egyesítették a gráf pontjait.
Ehhez az algoritmushoz olyan struktúrára van szükség, amely könnyen tudja kezelni, ha két komponenst egyesíteni kell, űgyanakkor gyorsan eldönthetővé teszi, hogy két pont azonos komponensben van-e, vagy különbözőben.
k) FÁK TOVÁBBI JELLEMZOI,
AZ ELVÁGÓPONT (CUTPOINT) FOGALMA
A most bebizonyított két tétel, amely szerint összefüggő n pontú gráfnak legalább n–1 éle van, körmentes n pontú gráfnak legfeljebb n–1 éle van, együtt ismét kiadja (E) állítás bizonyítását. Ez a gondolatmenet mutatja, hogy a fa egy úgynevezett „mini-max” tulajdonsággal bíró fogalom abban az értelemben, hogy egyszerre megoldása egy minimum- és egy maximum-kereső feladatnak. A körmentes gráfok közül ugyanis a fa élszáma a legnagyobb, míg az összefüggő gráfok közül a fáé a legkisebb. Ez magyarázza azt is, hogy miért játszik olyan fontos szerepet a gráfelméletben is, az algoritmuselméletben is.
Még egy féle módon kifejezhetjük azt, hogy a fának van egy minimum és egy maximum tulajdonsága is:
19. feladat:
Mutassuk meg, hogy ha G fa, akkor
a) bármely élét elhagyva megszűnik összefüggő lenni;
b) bármely új élt behúzva keletkezik benne kör;
c) egy tetszőleges x pontja pontosan akkor elsőfokú, ha G–x összefüggő.
MEGOLDÁS:
a) Az él két végpontja között nem marad út, hiszen a fában bármely két pont között pontosan egy út van, az él két végpontja között az él volt ez az egyetlen út.
b) A behúzott él két végpontját köti össze út a fában.
c) Ha d(x)=1, akkor az elhagyásával keletkező gráf is fa, mert körmentes gráf részgráfja is körmentes és az elsőfokú pont elhagyásával keletkező részgráf összefüggő marad. Ha viszont x-nek legalább két szomszédja van, legyenek ezek u és v. A fában u és v között is egyetlen út van, s ez az uxv út, amelyet x elhagyásával megszüntetünk. Tehát G–x gráfban u és v között nem fut él, azaz G–x nem lehet összefüggő.
DEFINÍCIÓ:
Az olyan pontot, amely elhagyásával az összefüggő gráf megszűnik összefüggő lenni, elvágó pontnak, vagy angol szóval cutpoint-nak nevezzük. A fenti c) állítás tehát azt mondja ki, hogy ha x legalább másodfokú pontja a fának, akkor x elvágó pont.
20. feladat:
Igaz-e, hogy ez utóbbi állítás jellemzi a fát? Azaz igaz-e, hogy ha egy összefüggő gráf bármely legalább másodfokú pontja cutpoint, akkor a gráf fa?
MEGOLDÁS:
A feladat állítása NEM IGAZ. Az alábbi gráf egy egyszerű ellenpélda:
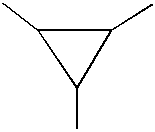
Ez a gráf bármely harmadfokú pont elhagyásával két komponensre esik szét (egy izolált pontra és egy 3 hosszú útra), de nem körmentes.
DEFINÍCIÓ:
Az olyan összefüggő gráfot, amelyben nincs cutpoint, vagyis amelyből bármely pontot elhagyva továbbra is összefüggő gráfot kapunk, kétszeresen összefüggő gráfnak nevezzük. Ezekkel külön fejezetben fogunk foglalkozni.