Az I/21. feladat megoldása:

49 pontú gráf van ezzel a tulajdonsággal: legyen x telített pont, azaz legyen összekötve minden más ponttal. A többi 48 pontot osszuk 24 párba és fusson egy-egy él a az azonos párba tartozó pontok között. (Ezt a gráfot megkaphatjuk úgy is, hogy 24 háromszöget illesztünk úgy össze, hogy egy csúcs mind a 24-ben közös legyen.) Ekkor bármely két ponthoz pontosan egy olyan pont van, amely mindkettőnek szomszédja. Hasonló konstrukció (n háromszög összeillesztésével) minden n-re ad egy 2n+1 pontú megfelelő gráfot. (Az ábra sematikus, út háromszöget rajzoltunk ki az n-bol.)

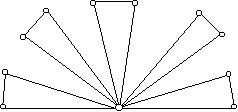
Megmutatjuk, hogy páros pontszám esetén nincs ilyen gráf.

1. MEGOLDÁS: Ha egy G gráfnak megvan az a tulajdonsága, hogy minden pontpárnak páratlan sok közös szomszédja van, akkor a gráfban minden pont foka páros. Legyen ugyanis x egy pont, V a szomszédainak halmaza. Ha y∈V, akkor y pontosan azokkal a pontokkal van összekötve V-ből, amelyek közös szomszédai x-nek és y-nak, s ezek száma páratlan. A V által feszített rászgráfban tehát minden pont foka páratlan. Ebből viszont a 20. feladat szerint következik , hogy V-nek páros sok pontja van.Legyen most x és y két tetszőleges pontja G-nek, legyen V_xy a közös szomszédaik halmaza, V_x x azon szomszédainak halmaza, amelyek nincsenek összekötve y-nal, V_y pedig y azon szomszédainak halmaza, amelyek nincsenek összekötve x-szel. A feltétel szerint |V_xy| páratlan, és láttuk, hogy x és y fokszáma, azaz |V_xy|+|V_x| és  |V_xy|+|V_y| páros, tehát |V_x| és |V_y| is páratlan. V_x,  V_y, V_xy páronként diszjunkt, tehát V_x∪V_y∪V_xy elemszáma páratlan.

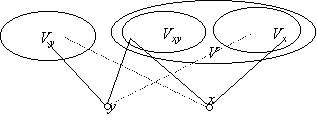
Minthogy a gráf pontszáma páros, a kimaradó pontok száma is páratlan, s ezek éppen azok a pontok, amelyek sem x-szel, sem y-nal nincsenek összekötve. Megjegyezzük, hogy ha x és y össze van kötve G-ben, akkor x benne van V_y-ban és y benne van V_x-ben, ekkor V_x∪ V_y∪ V_xy tartalmazza mindkettőt. Ha viszont x és y nincs összekötve, akkor egyiket sem tartalmazza (az ábra az utóbbi esetet mutatja). Mindkét esetben azt kapjuk, hogy páratlan azoknak a pontoknak a száma, amelyekkel sem x, sem y nincs összekötve és különböznek mindkettőtől. Vagyis: G komplementer gráfjának is megvan az a tulajdonsága, hogy bármely két pontjának páratlan sok közös szomszédja van. De akkor a komplementer gráfban is páros minden pont foka. Márpedig páros pontszámú gráfnál minden pont foka vagy a gráfban vagy komplementerében páratlan (lásd a 8. feladatot). Tehát a feladat feltételének csak olyan gráf felelhet meg, amelyben a pontok száma páratlan.

II. MEGOLDÁS: Ha már tudjuk, hogy a gráfban minden pont foka páros, a bizonyítást gyorsabban is befejezhetjük: vegyünk egy x pontot, legyen szomszédainak halmaza X. A kimaradó pontok száma páratlan, ezért az általuk feszített részgráfban van páros fokú pont, legyen ez y. Minthogy y foka is páros, ezért X-ből páros sok ponttal van összekötve (x-szel nincs összekötve), tehát x és y közös szomszédainak száma páros.

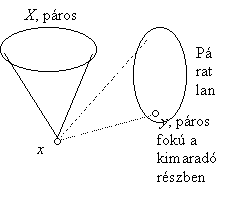
Ez az ellentmondás bizonyítja eredeti állításunkat.