I/27d) feladat megoldása:

d) igaz. Átfogalmazzuk a feladatot gráf-nyelvre: azt állítjuk, hogy ha egy véges egyszerű gráfban bármely két pontnak ugyanannyi közös szomszdéja van, akkor a gráf vagy reguláris, vagy van benne telített pont. Legyen x a gráf egy  tetszőleges pontja, legyen a fokszáma d és legyenek szomszédai x₁, x₂,…,x_d. Először megállapítjuk, hogy minden x_i-nek pontosan egy szomszédja van az x_j-k között. Ez abból következik, hogy x_i-nek és x-nek pontosan egy közös szomszédja van. Ha a gráfnak nincsenek további pontjai, akkor kész vagyunk. Ha vannak, akkor legyen A_i azoknak a pontoknak a halmaza, amelyek szomszédjai x_i-nek, és különböznek x-tol is, x_j-ktől is. Ha i és j különbözo, akkor A_i és A_j diszjunkt (különben x_i-nek és x_j-nek két közös szomszédja volna). Ha x_i és x_j között nem fut él, akkor A_i egy tetszőleges y pontjának és x_j-nek csak A_j-ben lehet közös szomszédja (hiszen x_j-nek szomszédja A_j-n kívül csak x és egy – x_i-tol feltevésünk szerint különböző – x_k lehet). Másrészt y nem lehet két A_j-belivel összekötve, mert ekkor y-nak és x_j-nek két közös szomszédja is volna. Tehát minden y∈A_i pontosan egy A_j-belivel van összekötve, ha x_ix_j nem éle a gráfnak. Természetesen ugyanez igaz i és j felcserélésével is, amiből viszont következik, hogy ha x_ix_j nem éle a gráfnak, akkor |A_i|=|A_j|.

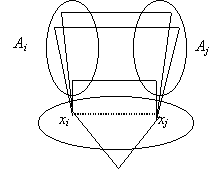
Ha viszont x_ix_j éle a gráfnak akkor y∈A_i és z∈A_j között nem mehet él, mert ezesetben x_iyzx_jx_i négyszög volna a gráfban, amit a feladat feltétele kizár. Végül ugyanígy látható be az is, hogy y∈A_i pontosan egy z∈A_i-beli ponttal van összekötve. Ebből viszont következik, hogy d(y)=1+d–1 (szomszédai: x_i, egy kivétellel minden A_j-ben egy pont, – A_i-ból is egy!). Tehát d minden olyan pont foka, amely valamelyik A_i-ben van. Mivel minden x-szel össze nem kötött pont benne van valamelyik A_i-ben, ezért minden olyan pont foka d, amely nincs összekötve x-szel. Ezzel azt is beláttuk, hogy bármely két össze nem kötött pont foka azonos. Be akarjuk látni, hogy ha sem x, sem szomszédai (tehát az x_i-k) nem telített pontok, akkor szomszédainak is d a foka.Ha x nem telített pont, akkor van olyan A_i, amely nem üres. Ennek minden pontja d-ed fokú. Másrészt nincs olyan x_i-től különböző x_j, amellyel valamely A_i-beli pont össze lenne kötve (különben x_i-nek és x_j-nek x-en kívül is volna közös szomszédja). Tehát minden x_i-től különböző x_j foka is megegyezik az A_i-beli pontok fokával, d-vel. Ezzel beláttuk, hogy minden x_i-től különböző pont foka d. Ha x_i nem telített pont, akkor van olyan pont, amellyel nincs összekötve, s ezzel megegyezik a foka, tehát x_i foka is d.Az állítás bizonyítását ezzel befejeztük.Azt is meg tudjuk mondani, hogy ha nincs telített pont, akkor milyen összefüggés áll fenn d és a pontszám között: minden A_i elemszáma d–2, tehát n=1+d+d(d–2)=d²–d+1. Ha d–1=p prím, akkor a p²+p+1 elemű véges geometriából lehet megfelelő gráfot csinálni: minden pontot a polárisának pontjaival kötünk össze (pontosan p+1=d ilyen pont van). Ismert, hogy ha egy P pont rajta van Q polárisán, akkor Q is rajta van P polárisán, tehát egyszerű (irányítatlan) gráfot kapunk. P és P’ közös szomszédja az a Q pont, amely rajta van P és P’ polárisán, vagyis Q a PP’ egyenes pólusa. Ilyen Q pedig pontosan egy van.