SURÁNYI LÁSZLÓ: GRÁFELMÉLET
I. fejezet/1.rész
GRÁFELMÉLETI ALAPFOGALMAK
a) A GRÁF FOGALMA, PONT, ÉL, FOKSZÁM
Tekintsük a következő feladatot:
1. feladat:
Egy társaságban lejátszottak néhány sakkmérkőzést. Bármely két ember legfeljebb egy mérkőzést játszott egymás ellen. Bizonyítsuk be, hogy mindenképpen volt két olyan ember, aki ugyanannyi emberrel mérkőzött meg.
MEGOLDÁS:
Legyen a társaság tagjainak száma n. Nézzük, egy ember hány mérkőzést játszhatott? Nyilvánvaló, hogy legfeljebb n–1-et, és elképzelhető az is, hogy egyet sem játszott, tehát az általa játszott mérkőzések száma 0-tól n–1-ig bármely egész szám lehet. Nem lehet azonban a társaságban egyszerre olyan, aki 0 mérkőzést játszott, és olyan, aki n–1 mérkőzést játszott, mert az előbbi senkivel nem játszott, az utóbbi mindenkivel játszott, tehát azzal is, aki 0 mérkőzést játszott. Tehát ha mindenkihez hozzárendeljük azt a számot, ahány mérkőzést játszott, akkor erre összesen legfeljebb n–1 lehetőség van: vagy az 1,2,…,n–1 számok közül kerül ki minden szám, vagy a 0,1,2,…,n–2 számok közül. A társaság tagjainak száma azonban n, tehát a „skatulyaelv” szerint van kettő, akihez ugyanazt a számot rendeltük, tehát ugyanannyi mérkőzést játszott.
MEGJEGYZÉS:
A bizonyításban feltettük, hogy a társaság tagjainak száma véges, amit egy társaságról joggal feltételezhetünk. A feltételt azért jegyeztük meg mégis, mert a feladatot át fogjuk fogalmazni, s az átfogalmazásban már nem magától értetődő ez a feltételezés.
1a. feladat:
Egy társaságban az ismeretségek kölcsönösek. Bizonyítsuk be, hogy van két ember, akinek ugyanannyi ismerőse van a társaságban.
MEGOLDÁS:
Legyen a társaság tagjainak száma n. A társaság tagjainak a társaságban 0-tól n–1 ismerőse lehet, ez n lehetőség. Nem lehet azonban a társaságban egyszerre olyan, akinek 0 ismerőse van és olyan, akinek n–1 ismerőse van, mert az előbbi senkit sem ismer, az utóbbi viszont mindenkit ismer. Tehát ismét összesen legfeljebb n–1 lehetőség van arra, hogy kinek hány ismerőse van. A társaság tagjainak száma azonban n, tehát a „skatulyaelv” szerint van kettő, akinek ugyanannyi ismerőse van.
Nyilvánvaló, hogy ez a megoldás nagyon hasonlít az előző feladat megoldásához. Ez nem véletlen, hiszen a feladat is bizonyos értelemben „ugyanaz”, mint az előző.
2. feladat:
Próbáljuk megfogalmazni, mit jelent itt az „ugyanaz” kifejezés!
A második feladatban csak az volt az érdekes, hogy két ember ismeri-e egymást vagy sem, az elsőben az az érdekes, hogy két ember játszott-e egymással vagy sem. A megoldás tehát pontosan ugyanaz lesz, ha az „ismerősök” száma helyett a „sakkpartnerek” számát tekintjük.
3. feladat:
Próbáljunk még olyan feladatokat megfogalmazni, amelyek „ugyanezt az állítást” rejtik magukban.
MEGOLDÁS:
Egy kézenfekvő állítás a következő:
3.a feladat:
Ha egy (véges) társaságban kölcsönösek az ismeretségek, akkor van két ember, aki ugyanannyi embert nem ismer.
Az 1a feladat állításához képest csak annyi a különbség, hogy itt az ismeretség helyett nem-ismeretség szerepel. De az állítás abban az értelemben sem új, hogy ha találtunk két embert, akinek ugyanannyi ismerőse van, akkor ezeknek ugyanannyi a „nem-ismerősük” is.
De képzeljük el, hogy a társaságban azok, akik még nem ismerik egymást, kezet fognak bemutatkozásul. Ekkor egy „új” állítást kapunk, amit rögtön általánosabban is kimondhatunk:
3.b feladat:
Egy társaságban némely emberek kezet fognak egymással. Ekkor biztosan van kettő, aki ugyanannyi emberrel fogott kezet.
Az eddigi „átfogalmazások” mind nagyon hasonlítanak: emberekről és azoknak egymáshoz való viszonyáról szóltak.
De tekinthetjük a következő állítást is:
3.c feladat:
Egy ország különböző repülőterei közül némelyeket közvetlen (oda-vissza) repülőjárat köt össze. Mutassuk meg, hogy van két repülőtér, amelyről ugyanannyi járat indul.
Ez a feladat is ugyanaz, mint az előzők, csakhogy most az emberek szerepét városok játsszák, az „ismeretségek”, a „mérkőzések” illetve a „kézfogások” szerepét a városokat összekötő repülőjáratok veszik át.
Természetesen számtalan további átfogalmazás is található: például vehetjük egy város telefonállomásait és nézhetjük azt, hogy melyikről hány másikkal beszéltek egy adott napon. Ekkor is igaz, hogy biztosan van kettő, amelyről ugyannyi másikkal beszéltek.
A BIZONYÍTÁS természetesen most is, mint mindegyik másik esetben ugyanaz:
Ha n telefonállomás van, akkor mindegyikről 0 és n–1 között valahányat hívtak fel. De az nem lehet, hogy valamelyikről egyáltalán nem beszéltek (0-val beszéltek), egy másikról pedig minden másikkal beszéltek (n–1 másikkal beszéltek), tehát most is csak n–1 lehetőség van tehát, s a „skatulyaelv” alkalmazásával most is kijön, hogy van kettő, amelyikről ugyanannyi másik állomással beszéltek.
Minden alkalommal ugyanaz a bizonyítás, ezért érdemes megkeresni, mi a közös a feladatokban. Ezt a közöset szemléltethetjük a következőképpen:
Ábrázoljuk az embereket, a városokat, illetve a telefonállomásokat egy-egy ponttal. Két embert ábrázoló pontot „összekötünk egy éllel” (azaz például egy egyenes szakasszal), ha játszottak egymással (az 1. feladat megfogalmazásában), ha ismerik egymást (az 1a feladat megfogalmazásában), ha nem ismerik egymást (3a feladat), illetve ha kezet fogtak egymással (3b feladat), két várost jelző pontot összekötünk egy éllel, ha van közöttük közvetlen repülőjárat (a 3c feladat esetében), illetve két telefonállomást jelző pontot összekötünk egy éllel, ha volt közöttük telefonkapcsolat az adott napon. Egyáltalán nem érdekes, hogy milyen alakja van az „élnek”, amellyel a pontokat összekötjük: lehet az él egy egyenes szakasz, de lehet egy görbe is, ennek semmilyen szerepe nincs, csak az számít, hogy „fut-e él” a két pont között vagy sem.

DEFINÍCIÓ:
Az így kapott ábrát – amely tehát pontokból és ezek közül némelyeket összekötő vonalakból áll, ahol a vonal alakjára nem vagyunk tekintettel – gráfnak nevezzük. A pontok a gráf pontjai vagy csúcsai, az összekötő vonalak a gráf élei.
A gráfot véges gráfnak nevezzük, ha a pontjainak száma véges.
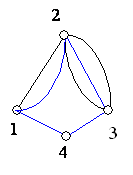
Ha összeszámoljuk, hány él indul ki egy pontból, akkor a kapott szám a pont fokszáma, vagy röviden foka. A fenti ábrán szereplő gráfnak négy csúcsa van, ezeket 1-től 4-ig számoztuk. Az 1-es pont (csúcs) csak a 3-assal van összekötve, viszont 3-as pont (csúcs) minden más ponttal (csúccsal) össze van kötve. Az 1-es pont fokszáma egy, a 2-esé és a 4-esé kettő, a 3-asé három.
Az x ponttal összekötött pontok az x pont szomszédai.
4.a feladat:
Fogalmazzuk meg az 1. feladatot és 3a, 3b, 3c átfogalmazásait gráfelméleti nyelven!
4.b feladat:
Nincsenek-e rejtett hiányosságok ebben a megfogalmazásban? Gondoljunk vissza arra, milyen feltételre volt szükségünk a sakkos megfogalmazásban!
MEGOLDÁS:
A sakkos megfogalmazásnál feltettük, hogy két ember nem játszott egymással több mérkőzést. Ez a gráfos megfogalmazásban azt jelenti, hogy feltettük: semelyik két pont között nem fut több él, vagy másképp fogalmazva: feltettük, hogy a gráfban nincs többszörös él. Feltettük azt is, hogy semelyik pont nincs önmagával összekötve (senki nem játszik önmagával), vagy másképp: a gráfban nincs hurokél.
DEFINÍCIÓ:
Egy gráf két pontja között futó
többszörös élről tehát akkor beszélünk, ha a két pont között több él is be van húzva, ha tehát az is fontos, hogy hányszor vannak összekötve.
Hurokélnek az olyan élt nevezzük, amelynek két végpontja azonos.
Ha egy gráfban nincs többszörös él és nincs hurokél, akkor a gráfot
egyszerű gráfnak nevezzük.
Egyszerű gráf esetén egy pont foka megegyezik szomszédainak számával. Tehát a végleges gráfelméleti megfogalmazás így hangzik:
Egy véges egyszerű gráfban (véges, többszörös él és hurokél nélküli gráfban) mindig van két olyan pont, amelyek fokszáma egyezik.
5. feladat:
Vajon mi a helyzet, ha megengedünk többszörös éleket is? Igaz-e, hogy ha a sakkos megfogalmazásban megengedjük, hogy némelyek többször is játszottak egymással, akkor is biztosan van két olyan ember, akik ugyanannyi sakkpartit játszottak? Az előző feladatunk megoldása nagyon erősen használta, hogy a gráf egyszerű, tehát a fokszámok csak 0 és n–1 között változhatnak. Ha viszont megengedünk többszörös éleket is, akkor a fokszám bármilyen nagy lehet, a bizonyításunk tehát nem működik. Vajon csak a bizonyítás nem működik, vagy az állítás sem igaz?
MEGOLDÁS:
Most könnyű ellenpéldát csinálni: tegyük fel például, hogy a társaságban csak három ember van, A,B és C. Tegyük fel, hogy A és B egy mérkőzést játszott egymással, B és C kettőt, A és C egyet sem. Ekkor A 1, B 3, C 2 mérkőzést játszott.

5.a feladat:
Ez mindenesetre ellenpélda három pont (résztvevő) esetén. De van-e akárhány pont (résztvevő) esetén is ellenpélda?
MEGOLDÁS:
Négy pontra a következőképpen lehet ellenpéldát csinálni: felvesszük az előbbi gráfot, tehát egy hárompontú gráfot, ahol az 1-es és 2-es között 1 él fut, a 2-es és 3-as között pedig kettő.

Felveszünk továbbá egy negyedik pontot, amelyből nem fut ki él:

Ezután berajzolunk a gráfba még egy olyan „kört”, amely minden ponton átmegy (úgynevezett Hamilton-kört , lásd a III. fejezetet), vagyis hozzáveszünk a gráfhoz például egy-egy 12, 23, 34, 41 élt (ahol már van, ott egy-egy további ilyen élt): ekkor 1 és 2 között két él fut, 2 és 3 között 3 él fut, a 3-as és 4-es pont között valamint a 4-es és az 1-es között egy-egy él fut. Most az 1-es pont fokszáma 3, a 2-esé 5, a 3-asé 4, a négyesé 2:
Vegyük észre, hogy ez az eljárás akárhány pontra folytatható. Tegyük fel, hogy már van egy olyan gráfunk, amelyben n–1 pont van és ezek fokszámai mind különböző pozitív számok. Vegyünk hozzá a gráfhoz egy pontot, amelyből nem indul ki él, így kapunk egy olyan gráfot, amelyben n pont van, és bármely két pont fokszáma különbözik. Ebből azonban még nem tudnánk továbbmenni, ezért illesszünk a gráfra egy Hamilton-kört, vagyis egy-egy olyan új élt, amely az 1-es és 2-es, a 2-es és 3-as, a 3-as és 4-es, …, az n–2-es és n–1-es, az n–1-es és n-es, végül az n-es és 1-es pontot köti össze. Ekkor minden pont fokszáma pontosan kettővel nő, tehát továbbra is minden pont fokszáma különböző lesz, de most már minden pont fokszáma pozitív (sőt: legalább kettő). Ezzel minden n-re találtunk olyan n pontú nem egyszerű gráfot, amelyben nincs két azonos fokszámú pont.
Megjegyezzük, hogy a konstrukcióban lényegében használtuk már a kör fogalmát, erre a II. fejezetben térünk vissza. Sőt, a Hamilton körét is, erről részletesebben egy későbbi fejezetben lesz szó. Használtunk azonban egy olyan fogalmat is, amelyre lépten-nyomon szükségünk van:
DEFINÍCIÓ:
Az olyan pontot, amelyből nem indul ki él, izolált pontnak nevezik.
Most teszünk egy kitérőt a végtelen gráfok irányába: megvizsgáljuk, igaz-e ott is az állításunk?
6. feladat:
Említettük már, hogy elképzelhető az is, hogy a gráfnak nem véges sok csúcsa van, hanem végtelen sok. Mi a helyzet ekkor? Igaz-e végtelen egyszerű gráfokra az állítás? Az 1. feladat megoldása a végességet is nagyon használta. Végtelen (megszámlálhatóan végtelen) sok pont esetén ugyanis a fokszám végtelen is lehet, s ekkor nem világos, hogy mit jelent, hogy „ugyanakkora a fokszám”. De ha kikötjük, hogy minden pont foka véges legyen, akkor is a fokszám bármilyen nemnegatív egész szám lehet, a skatulyaelv tehát nem működik. De vajon igaz marad-e az állítás?
MEGOLDÁS:
Megmutatjuk, hogy az állítás végtelen gráfokra nem igaz. Van ugyanis olyan végtelen egyszerű gráf, amelyben minden pont fokszáma különböző. Legyenek a gráf pontjai az 1, 2, 3, 4, … pozitív egész számok. Olyan gráfot akarunk csinálni, amelyben az i-edik csúcspont fokszáma éppen i. Minden pontra ráírjuk tehát a sorszámát, hogy tudjuk: ekkorára akarjuk a fokszámát. Ezután először összekötjük az 1-es pontot a 2-es ponttal. Ezzel az 1-es pont fokszáma megfelelő lett, őt tehát kihúzzuk és a 2-esre most 1-et írunk: még ennyi „hiányzik a fokszámából”, a többi pontra írt szám változatlan marad. Ezután sorra vesszük a 2-es pontot, ezt további 1 ponttal kell összekötnünk, összekötjük a 3-as ponttal. Elhagyjuk a 2-es pontot, hiszen most már az ő fokszáma is megfelelő és a 3-as pontra eggyel kevesebbet írunk. Most sorra vesszük a 3-as pontot, ezen jelenleg 2-es szám áll, ennyi élt kell még belőle behúznunk: összekötjük a 4-es és 5-ös ponttal, majd az ezekre írt számot csökkentjük eggyel és elhagyjuk a 3-as pontot. Így minden lépésben sorra vesszük a következő pontot, ha a pillanatnyilag rajta szereplő szám i, akkor összekötjük i olyan ponttal, amelyen jelenleg pozitív szám áll. Ezután ezt a pontot elhagyhatjuk, és a vele most összekötött pontokra írt számot eggyel csökkentjük. (Ha i=0 volt, akkor e szerint az eljárás szerint egyszerűen elhagyjuk a pontot, mert már „rendben van”.) Ezt az eljárást minden egyes pontra elvégezve egy olyan gráfhoz jutunk, amelyben az i-edik pont fokszáma pontosan i. (Az ábrán azt az állapotot rajzoltuk fel, amikor az első négy pont fokszáma már „rendben van”, az 5-ös pontból a 6-osba, 7-esbe és 8-asba kell majd berajzolni élt.)

7. feladat:
Egy város telefonközpontjában számontartják, hogy a központhoz tartozó telefonállomások mindegyikéről hány másikat hívtak fel aznap (ha egy állomást többször is felhívtak, azt is csak egynek számítják). Igaz-e, hogy van két telefonállomás, amelyről ugyanannyit hívtak?
Most sincs hurokél (egy telefonállomásról sem hívható fel önmaga), és (látszólag) nincs többszörös él sem – legalábbis látszólag – hiszen ha egy állomást többször hívtak egy helyről, azt is csak egy hívásnak számítjuk. De egyféleképp mégis lehetséges: ha az a állomásról felhívták b-t és a b állomásról is felhívták a-t, ami könnyen előfordulhat. Ez rögtön felhívja a figyelmet arra, hogy itt NEM az eddigi értelemben vett gráfról van szó. Itt is pontok vannak és itt is az az érdekes, hogy két pont össze van-e kötve, vagy sincs, de itt NEM MINDEGY, HOGY MELYIK PONTBÓL „INDUL” AZ ÉL ÉS MELYIKBE ÉRKEZIK. Vagyis: itt IRÁNYÍTANI kell a gráf éleit. Az a-ból b-be induló él nem azonos a b-ből a-ba induló éllel.
DEFINÍCIÓ:
Az ilyen gráfot, ahol az élek irányítva vannak, ahol nem elég megmondani, hogy melyik pontok vannak éllel összekötve, hanem azt is meg kell mondani minden élről, hogy melyik a kezdőpontja és melyik a végpontja, irányított gráfnak nevezik. Az irányított gráfban minden pontnak van egy kifoka: ez azt mondja meg, hány él indul ki a pontból, és van egy befoka: ez azt mondja meg, hány él érkezik be a pontba.
A 7. feladat kérdése tehát így fogalmazható meg gráfelméleti nyelven:
7.a feladat:
Igaz-e, hogy egy irányított gráfban mindig van két pont, amelynek ugyanakkora a kifoka?
MEGOLDÁS:
Képzeljük el, hogy a gráf pontjait sorba megszámozzuk, ha n pont van, akkor 1-től n-ig terjed a számozás. Tegyük fel, hogy minden egyes pontból indul ki él az összes nagyobb számú pontba, viszont nem indul él egyetlen kisebb számú pontba sem. Ekkor az 1-es számú pontból n–1 él indul ki, a 2-es számú pontból n–2 él indul ki, s általában az i-es számú pontból n–i él indul ki, az n-edik pontból egy él sem indul ki. Vagyis minden pont kifoka különböző. Az állítás tehát nem igaz! (Az ábra n=5-re mutatja az ellenpéldát.)
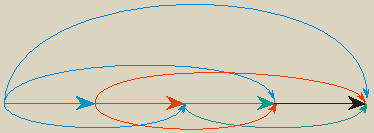
Érdemes elgondolkodni azon, hogy van-e más ellenpélda.
b) A KOMPLEMENTERGRÁF FOGALMA;
TELJES ÉS ÜRES GRÁF
Az 1a. feladat esetében azt a gráfot tekintettük, amelyben a pontok az emberek, és két pontot akkor kötünk össze éllel, ha a nekik megfelelő emberek ismerik egymást. A 3a feladatban és a „kézfogós” feladatnál viszont azt a gráfot tekintettük, amelyben két pontot akkor kötünk össze éllel, ha a nekik megfelelő emberek nem ismerik egymást. Ez a két gráf egymás komplementere. Vagyis
DEFINÍCIÓ:
A G gráf komplementere az a gráf, amelynek pontjai megegyeznek G pontjaival, és amelyben két pont pontosan akkor van összekötve éllel, ha G-ben nincs összekötve.
PÉLDÁK:
Legyen például a G gráf egy háromszög, azaz legyen olyan hárompontú gráf, amelyben bármely két pont között fut él. Ekkor G komplementere a hárompontú üres gráf.
Általában is igaz, hogy ha Kn-nel jelöljük az n pontú teljes gráfot, azaz azt az n pontú gráfot, amelyben bármely két pontot él köt össze, akkor Kn komplementere az n pontú üres gráf, tehát az az n pontú gráf, amelyben egyetlen él sincs behúzva.
Ha G négypontú, és pontjai A,B,C,D, és élei egy „kört” alkotnak, vagyis élei AB,BC,CD,DA, akkor a komplementer gráf az a négypontú gráf, amelynek két éle AC és BD.
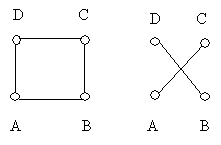
8. feladat:
Bizonyítsuk be, hogy ha egy (egyszerű véges) gráfnak páratlan sok pontja van, akkor bármely pont fokszámának paritása azonos G-ben és a komplementerében. Ha a gráfnak páros sok pontja van, akkor bármely pontnak vagy G-ben, vagy G komplementerében páratlan a fokszáma.
MEGOLDÁS:
Legyen a gráf pontjainak száma n, és egy tetszőleges x pontjának fokszáma G-ben d. Ekkor x fokszáma G komplementerében n–1–d, tehát x pontjának fokszámát G-ben és G komplementerében összeadva pontosan n–1-et kapunk. Ha n páros, akkor n–1 páratlan, tehát a két fokszám közül pontosan az egyik páros, a másik páratlan. Ha n páratlan, akkor n–1 páros, így a két fokszám paritása azonos.
MEGJEGYZÉS:
Ehhez a feladathoz kapcsolódik az I/28 feladat.
c) ÖSSZEFÜGGÉS AZ ÉLSZÁM ÉS A FOKSZÁMOK KÖZÖTT: EULER TÉTELE;
REGULÁRIS GRÁFOK
A gráfok élszáma és pontjainak fokszáma között nyilván van összefüggés. A következő feladatok ezt az összefüggést vannak hivatva megvilágítani. Vizsgáljuk meg először a teljes gráfot:
9. feladat:
Hány éle van egy n pontú teljes gráfnak?
Az I/9. feladat megoldása:
I: MEGOLDÁS: Bárhogyan veszünk két csúcsot a teljes gráfból, ezek össze vannak kötve éllel. Az n pontú teljes gráfnak tehát annyi éle van, ahány féleképpen n elemből ki tudunk választani kettőt. Vagyis:
Az n pontú teljes gráf élszáma pontosan n(n–1)/2.
2. BIZONYÍTÁS: Számolhatunk így is:
Minden pontból n–1 él indul ki, ez n(n–1) él, de így minden élt kétszer számolunk, tehát az élek száma ennek a fele.
10. feladat:
Lehetséges-e, hogy egy 50 tagú társaságban mindenki pontosan három embert ismerjen? Lehetséges-e ez, ha a társaságnak 51 tagja van? És ha 100? És ha 99?
Hogyan fogalmazható meg a feladat gráfokra? Milyen n számokra van olyan társaság, amelyben mindenki pontosan három másik embert ismer?
MEGOLDÁS:
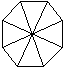
Tegyük fel, hogy van ötven ember, akik közül senki nem ismeri a másikat. Ültessük le őket egy kerek asztal mellé és mutassuk be egymásnak azokat, akik egymás mellett ülnek, valamint mutassuk be egymásnak az egymással szemben ülőket: az elsőt a 26.-nak, a másodikat a 27.-nek, és általában az i-ediket a 25+i-ediknek. Ekkor minden embernek pontosan három ismerőse lesz. Az első kérdésre tehát igen a válasz. Hasonlóan okoskodhatunk száztagú társaság esetén és általában bármilyen páros tagú társaság esetén. Tegyük fel, hogy van 2n ember, akik közül senki nem ismer senkit. Leültetjük őket egy kerek asztal köré, ismét bemutatjuk egymásnak az egymás mellett ülőket és az egymással szemben ülőket. (Most két ember akkor ül egymással szemben, ha a sorszámuk között pontosan n a különbség.) Így kapunk egy olyan 2n tagú társaságot, ahol minden ember három másikat ismer. (Az ábra n=4-re, azaz nyolctagú társaságra mutatja a konstrukciót.)
Ha viszont 51 (99, vagy általában páratlan sok: 2n+1) tagja van a társaságnak, akkor nem lehetséges, hogy mindenki pontosan három másik embert ismerjen. Számoljuk ugyanis össze, hány ismeretség lenne ez esetben. Mindenki három másikat ismer, ez 51·3 (99·3, (2n+1)·3), viszont így minden ismeretséget kétszer számolunk, hiszen az ismeretség „mindkét résztvevőjénél” megszámoltuk. Vagyis az ismeretségek száma 51·3/2 (99·3/2, (2n+1)·3/2), ami nem egész szám, s ez lehetetlen.
Ha a kapott állítást átfogalmazzuk gráfelméleti nyelvre, azt kapjuk, hogy páros n-re van n pontú gráf, amelyben minden pont foka három, páratlan n-re nincs.
DEFINÍCIÓ:
Azokat a gráfokat, amelyekben minden pont foka azonos, reguláris gráfnak nevezzük. Ha minden pont foka d, akkor a gráf d-reguláris.
Ezek szerint előző megállapításunk így is fogalmazható:
Ha n páros, akkor van n pontú 3-reguláris gráf, ha n páratlan, akkor nincs.
A feladat folytatása: I/19
11. feladat:
Végigkérdeztük egy nyolctagú társaság tagjait, hogy ki hány másik embert ismer, és a következő válaszokat kaptuk: 3,5,4,2,5,2,4,4. Lehetséges-e ez, ha az ismeretségek kölcsönösek?
MEGOLDÁS:
Nem lehet, mert ha összeadjuk az ismeretségek számát, akkor 3+5+2+4+5+2+4+4 = 29 páratlan szám, viszont ha az ismeretségek kölcsönösek, akkor minden ismeretséget kétszer kellett számolnunk, vagyis az összegnek párosnak kell lennie.
Az utolsó három feladatban visszatér ugyanaz az ötlet, próbáljuk megfogalmazni, hogy mi volt ez az ötlet:
12. feladat:
Adjuk össze egy gráfban a pontok fokszámát, mit állíthatunk a kapott számról?
MEGOLDÁS:
Véges gráfban a fokszámok összege éppen az élszám kétszerese, hiszen minden élt pontosan kétszer számoltunk össze: a két végpontjánál.
Ez az élszámra vonatkozó Euler-tétel.
Az Euler-tétel egyszerű következménye tehát a következő:
Véges egyszerű gráfban a fokszámok összege mindenképpen páros szám.
További az Euler-tételre vonatkozó feladatok: I/19, I/20
Kapcsolódó feladatok: I/21, I/22, I/28, I/29, I/30
12.a feladat:
Igaz-e Euler tétele többszörös éleket is tartalmazó gráfban?
Az I/12.a feladat megoldása:
Ha a gráfban nincs hurokél, akkor a fokszámok összeadásánál minden élt kétszer számolunk: a két végpontjánál. Tehát a fokszámok összege most is az élszám kétszerese, az Euler-tétel többszörös élek esetén is igaz. Ha viszont hurokélek is vannak, azokat a fokszámnál kétszeresen kell számolnunk (mintha kezdőpontjuknál is, végpontjuknál is megszámolnánk), csak így marad érvényben Euler tétele.
13. feladat:
Lehet-e bármely páros szám a fokszámok összege?
MEGOLDÁSA:
Könnyen beláthatjuk, hogy bármely páros szám lehet a fokszámok összege. Ez az állítás egyenértékű azzal, hogy az élek száma bármilyen pozitív egész n szám lehet. Ez viszont igaz, hiszen ha veszünk n+1 pontot és egy pontot összekötünk minden másikkal, az így kapott úgynevezett csillag gráfnak pontosan n éle van.
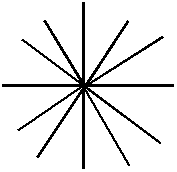
d) FÜGGETLEN PONTOK
14. feladat:
Egy 111 tagú társaságban mindenki legfeljebb tíz embert ismer. Mutassuk meg, hogy van a társaságban 11 ember, akik közül senki nem ismeri a másik tizet. Igaz-e ez minden 110 tagú társaságban is, ha mindenki legfeljebb tíz embert ismer? Van-e mindig 12 ilyen ember is?
MEGOLDÁS:
Mohó algoritmust fogunk használni. Válasszunk ki egy tetszőleges embert, ő lesz E1, és állítsuk félre összes ismerősét. Legfeljebb tíz ismerőse van, így marad még (rajta kívül) legalább száz ember. Válasszunk ki ezek közül is egy tetszőleges E2 embert és állítsuk félre E2 összes ismerősét is. Így megint legfeljebb tízet állítottunk félre, tehát marad még (a két kiválasztotton és a legfeljebb 20 félreállítotton kívül) legalább 89 ember. Ezt az eljárást folytatva minden lépésben kiválasztunk egy új embert (az i-edik lépésben Ei-t) és félre állítjuk az ismerőseit. A (félreállítottakon és kiválasztottakon kívül) maradó emberek nem ismerik az addig kiválasztottakat. (Ezért az újonnan kiválasztott ember sem ismerheti a régebben kiválasztottakat.) A még választható emberek (=maradó) száma minden lépésben legfeljebb 11-gyel csökken. Vagyis a tíz ember kiválasztása után még mindig marad egy, aki az előző tízet nem ismeri. Tehát legalább 11 embert sikerül kiválasztanunk, hogy közülük senki ne ismerjen senkit.
Ha a 110 ember olyan 11 fős „klikkeket” alkot, akik kölcsönösen ismerik egymást, viszont két klikk emberei közül senki nem ismer senkit, akkor ebből a társaságból nem lehet 10-nél több embert kiválasztani, hiszen minden „klikkből” csak egy embert választhatunk. Az állítás tehát ebben az irányban nem javítható. Másrészt ha e 110 tagú társasághoz hozzáveszünk még egy 11 tagú „klikket”, akkor az így kapott 11 „klikk” mindegyikéből csak egy embert választhatunk, tehát még 121 tagú társaságra sem mindig igaz, hogy kiválasztható 12 megfelelő ember. Az állítás tehát mindkét irányban éles. Pontosabban még 120 emberre is igaz, hogy 11 megfelelő ember van benne, de 12 már nincs.
Gráfelméleti nyelven azt bizonyítottuk be, hogy
ha egy 111 pontú gráfban minden pont foka legfeljebb tíz, akkor van 11 pont, amelyek közül semelyik kettő között nem fut él, és ugyanez nem minden 110 pontú gráfra igaz.
DEFINÍCIÓ:
Az olyan csúcshalmazt, amelyben semelyik két pont között nem fut él, a gráf független ponthalmazának nevezzük.
A fenti bizonyítás általában azt adja, hogy ha egy 11k+1 pontú gráfban minden pont foka legfeljebb tíz, akkor van k+1 független pont.
15. feladat:
Hogyan általánosítható tovább ez a feladat?
MEGOLDÁS:
Nyilván ugyanígy igazolható általában, hogy
ha egy n pontú gráfban minden pont foka legfeljebb d, akkor a gráfban van legalább n/(d+1) olyan pont, amelyek közül semelyik kettő nincs összekötve, vagyis van legalább n/(d+1) független pont a gráfban.
Az eljárás most is ugyanaz: minden lépésben kiválasztunk egy pontot és elhagyjuk a szomszédait, így d+1 ponttal kevesebb marad és a maradó pontok közül egy sincs összekötve a már kiválasztott pontokkal. K lépés után K(d+1) pontot hagytunk el, amíg tehát K < n/(d+1), addig marad még kiválasztható pont.
16. feladat*:
Egy 3n tagú társaságban bármely két embernek van közös ismerőse. Bizonyítsuk be, hogy kiválasztható n ember, amelyek együttesen az összes többit ismerik.
MEGOLDÁS:
A feladat feltétele átfogalmazható úgy, hogy ha A a társaság egy tetszőleges tagja, a társaság bármely tagjának van ismerőse A ismerősei között. Ha tehát A-nak legfeljebb n ismerőse van, akkor az ő ismerőseit kiválaszthatjuk, s ezek együtt a társaság összes tagját ismerik.
Ha viszont bármely ember legalább n+1 másikat ismer, akkor A is legalább n+1 embert ismer. A maradó 2n–2 embert valahogyan párokba állítjuk, és bármely kettőnek van közös ismerőse, ez n–1 ember, ők A-val együtt az az n ember, akik együtt ismerik a többit. (Valójában A-n kívül mindenkinek van közöttük ismerőse.)
MEGJEGYZÉS:
Felmerül a kérdés, hogy nem elég-e kevesebb ember is. Erre válaszol a 26. feladat. További kérdés, hogy a feladat feltétele nem gyengíthető-e. Erre a II. fejezet 57. feladatában térünk vissza.









