Az I/37. feladat megoldása:

A gráf pontjai szerinti teljes indukciót alkalmazunk. Ha minden pont foka páros, akkor nincs mit bizonyítanunk. Ha van egy x páratlan fokú pont, akkor legyen S a szomszédainak halmaza, T a többi pont. Vegyük az S által feszített gráf komplementerét, és vegyük hozzá az ST és a TT éleket. (Az ábrán a komplementer éleit kékkel jelöltük.)

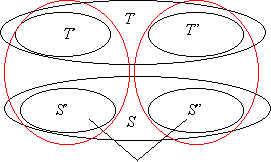
Az így kapott G’ gráfra alkalmazzuk az indukciós feltételt: két részre bontható S=S’+S” és T=T’+T” úgy, hogy az S’∪T’ és az S”∪T” által G’-ben feszített részgráfokban minden pont foka páros. S’ és S” közül az egyik páratlan sok pontból áll, mondjuk S’. Ekkor S” páros sok pontból áll. Cseréljük most vissza S’-ben és S”-ben az éleket az eredeti élekre és tegyük hozzá x-et S’-höz. Ekkor S”-ben marad minden fok paritása, és S’-ben minden fok paritása megfordulna, de hozzávettük x-et, amellyel mind össze van kötve. Ezzel a bizonyítást befejeztük.