SURÁNYI LÁSZLÓ: Gráfelmélet I. fejezet/2.
MEGOLDÁSOK (az első szóra kattintva elérhető a feladat szövege):
17.
A házastársával senki nem fog kezet, ezért a kilenc megkérdezett csak úgy mondhat csupa különböző számot, ha rendre 0,1,2,3,4,5,6,7,8-at mondanak. Aki nyolcat mond, az a házastársán kívül mindenkivel kezett fogott, így nullát csak a házastársa mondhatott. Aki hetet mondott, az a házastársán és a nulláson kívül mindenkivel kezet fogott, így csak az ő házastársa mondhatott egyet (a többiek már legalább kettővel: a nyolcassal és a hetessel kezet fogtak).

Az eljárást folytatva azt kapjuk, hogy a hatos és a kettes, az ötös és a hármas házastársak, a négyesnek pedig a házastársa is néggyel fogott kezet. Tehát a két négyes a Kovács-házaspár. Tehát mindketten négy emberrel fogtak kezet.
18.
A házastársával senki nem fog kezet, ezért az öt megkérdezett csak úgy mondhat csupa különböző számot, ha rendre 0,1,2,3,4 volt a válaszuk. Ez összesen tíz kéznyújtás, viszont összesen 6·4/2=12-szer nyújtottak kezet (egy kézfogásnál mindkét fél kezet nyújt!). Vagyis Kovácsné kétszer nyújtott kezet, tehát érkezésekor ketten voltak már ott, és esetleg még házastársa. Vagyis harmadiknak vagy negyediknek érkezhetett. Mindkét eset lehetséges. Ha például az érkezési sorrend: A,B,C,a,b,c (az azonos betűk jelölik a házastársakat), akkor az érkező kéznyújtásainak száma: 0,1,2,2,3,4. Kovácsné lehet C vagy a.
19.
A 10. feladatban a háromról csak annyit használtunk fel, hogy páratlan, tehát általában is igaz, hogy
Ha n páratlan és d is, akkor nincs n pontú, d-reguláris gráf.
Ha ugyanis volna, akkor minden pontból d él indulna ki, ez nd él, de így minden élt kétszer számoltunk, tehát az élszám nd/2 volna, s ez nem egész szám, ami lehetetlen.
Ha viszont n és d közül legalább az egyik páros, akkor már van n pontú d-reguláris gráf.
Egy ilyet a következő képpen lehet csinálni.
Legyen először n tetszőleges és d=2D páros. Képzeljük most egymást nem ismerő embereknek a gráf pontjait, és ültessük le őket ismét egy kerek asztal köré. Ismertessünk össze mindenkit a tőle jobbra és balra 1, 2, …, D távolságra ülőkkel. Ha például d=6 (D=3), akkor mindenkit összeismertetünk a bal és jobb oldali szomszédjával, másodszomszédjával és harmadszomszédjával. Így mindenkinek pontosan 2D ismerőse lesz. (Meg kell még gondolnunk, hogy ha egy E embert bemutattunk egy E’ embernek, akkor E’-t is bemutattuk E-nek, különben nem lennének kölcsönösek az ismeretségek, tehát nem beszélhetnénk – irányítatlan – gráfról.) Mindez persze csak akkor megy, ha az a 2D ember, akit így sorra veszünk, mind különböző, vagyis ha n>2D, azaz n legalább d+1.
Ha rögtön gráfelméleti nyelven akarjuk elmondani a konstrukciót, akkor mondhatjuk a következőt: Legyenek a gráf pontjai egy szabályos n-szög csúcsai, és számozzuk meg őket 1-től n-ig: P1, P2, …, Pn, és egyezzünk meg abban, hogy Pn+1=P1, Pn+2=P2, s általában Pn+k=Pk. Kössünk össze két pontot, ha a sorszámuk különbsége 1, 2, …, D. (Így például P1 össze lesz kötve P2-vel, P3-mal, …., PD+1-gyel, de össze lesz kötve Pn-nel, Pn–1-gyel, …, Pn–D+1-gyel is (mert P1=Pn+1). Így minden pont fokszáma éppen 2D lesz. Megint fel kell tenni, hogy n legalább d+1 és megint meg kell gondolni, hogy ha egy Pi pontot összekötöttünk egy Pk ponttal, akkor a Pk pontot is összekötöttük a Pi ponttal.
Marad az az eset, ha
n=2
m páros,
d páratlan. Ekkor
d–1=2
D páros, tehát megcsinálhatjuk az előző konstrukciót, majd még minden pontot összekötünk a vele szemben levővel, vagyis az
i-ediket az
m+
i-edikkel. Itt persze fel kell tennünk, hogy ezzel a ponttal még nem volt összekötve, tehát hogy
m>
D, azaz
n=2
m>2
D, vagyis
n legalább 2
D+2=
d+1. (Az ábra
D=2-re mutatja a gráf egy darabját.)
Összefoglalva azt kapjuk, hogy ha
n³d+1 és
n és
d közül legalább az egyik páros, akkor van (egyszerű)
n pontú
d-reguláris gráf, ha viszont
n is,
d is páros, akkor nincs.
20.
Ez egyszerűen következik Eulernek a 12. feladatban bizonyított tételéből: e szerint a fokszámösszeg páros. Márpedig csak úgy lehet páros, ha a páratlan fokszámú pontok száma páros.
21. A lányok szerint összesen 3+1+2+2 = 8 féle táncospár volt, viszont a fiúk szerint 2+2+3+2 = 9, ez ellentmondás, tehát legalább egy valaki biztosan tévedett.
22.
a) Az első esetben a lányok adatait összeadva azt kapjuk, hogy biztosan páros sok táncospár alakult ki az este folyamán, hiszen 21 darab páros számot kell összeadnunk, hogy megkapjuk az összes táncospár számát. Ha viszont minden fiú három vagy öt lánnyal táncolt volna, akkor az ő adataikat összeadva páratlan sok páratlan számot kellene összeadnunk, s így biztos páratlan számot kapnánk, ami ellentmondás volna.
b) Ez a feladat szinte ugyanaz, mint az előző. Ha azt nézzük, hogy ki hány levelet írt (ha valaki egy társának több levelet is írt, azt is csak egynek számoljuk), akkor azt kapjuk, hogy összesen páros sok levelet írtak. Ha viszont mindenki három vagy öt levelet kapna, akkor a kapott levelek száma páratlan lenne, tehát összesen nem ugyanannyi levelet írtak volna, mint amennyit kaptak. (Feltettük, hogy a postán nem kallódik el levél.)
23.
Minden irányított gráfhoz hozzárendelhető egy páros gráf a következőképpen: az irányított gráf pontjait megduplázzuk. Az egyik „osztály” lesz a kezdőpontok halmaza, a másik osztály lesz a végpontok halmaza. Tehát minden irányított élnek megfeleltetjük a páros gráf egy irányítatlan élét, amely a megfelelő kezdőpontból (az első osztályba tartozó pontból) indul ki és a megfelelő végpontba (a második osztályba tartozó pontba) érkezik. Vagyis: számozzuk meg az irányított gráf pontjait 1-től n-ig, majd a páros gráf mindkét osztályának pontjait is számozzuk meg 1-től n-ig. Az i-edik pontból a j-edik pontba mutató irányított élnek a páros gráfban azt az élt feleltetjük meg, amely az első osztály i-edik pontját a második osztály j-edik pontjával köti össze. Nyilvánvaló, hogy erről a páros gráfról „visszaolvasható” az eredeti irányított gráf.
Másrészt így mindig olyan páros gráfot kapunk, amelynek két osztályában ugyanannyi pont van. Vagyis:
a megadott megfeleltetés egyértelmű megfeleltetés az irányított gráfok és az olyan páros gráfok között, amelyeknek két osztályában ugyanannyi pont van.
24.
Osszuk „klikkekre” a társaságot úgy, hogy az egy osztályba járók alkossanak egy klikket. Aki hármat mond, az egy négy fős klikkbe tartozik, s mivel öten mondtak hármat, legalább két négy fős klikk van. Aki négyet mond, az egy-egy öt fős klikkbe tartozik, s mivel nyolcan mondták, így legalább két öt fős klikk is van, ez már összesen 4+4+5+5=18 ember. A társaságban még hárman vannak, akik e négy klikk egyikébe sem tartoznak. Mindegyikük egy legalább két fős klikkhez csak úgy tartozhat, ha ők egy három fős klikket alkotnak. Tehát a hiányzó számok: még három hármas, két négyes és három kettes.
25.
Mindenki legfeljebb két másikat nem ismer, három személy esetében legfeljebb hat olyan van, akit legalább egyikük nem ismer. 3+6=9, még marad egy valaki, aki mindhármukat ismeri.
Általánosítás: Vegyünk egy n tagú társaságot, azt akarjuk, hogy bármely k embernek legyen közös ismerőse, s ehhez olyan feltételt akarunk megadni, hogy bármelyikük legalább d másikat ismerjen. Az a kérdés, hogy mekkorára kell választanunk d-t. Ha mindenki legalább d másikat ismer, akkor legfeljebb n–d–1-et nem ismer. Ez k ember esetében k(n–d–1) ember. Ehhez jön még az a k ember, akinek a közös ismerősét keressük, ez összesen legfeljebb k(n–d) ember. Akkor van biztosan közös ismerősük, ha ez a szám kisebb n-nél, vagyis ha
k(n–d) < n, ahonnan
d > (k–1)n/k.
Azt kaptuk, hogy ha egy n tagú társaságban mindenki több, mint (k-1)n/k másikat ismer, akkor bármely k embernek van közös ismerőse.
Gráfelméleti nyelven:
ha egy n pontú (egyszerű) gráfban minden pont foka nagyobb, mint (k–1)n/k, akkor bármely k ponthoz található olyan pont, amellyel egyik sincsen összekötve.
26.
A megoldáshoz ismételjük el a 16. feladatra adott bizonyítást, mert ebből fogunk továbblépni:
Ha van egy ember, aki legfeljebb n másikat ismer, akkor ez az n ember együttesen mindenki mást ismer. Ha viszont bármely ember legalább n+1 másikat ismer, válasszunk ki egy x embert. Ő ismer legalább n+1 embert. A maradó 2n–2 embert valahogyan párokba állítjuk, és bármely kettőnek van közös ismerőse, ez n–1 ember, ők x-szel az az n ember, akik együtt ismerik a többit.
Ugyanez a gondolatmenet azt adja, hogy legfeljebb 4n2/3 ember is kiválasztható úgy, hogy azok együtt mindenkit ismerjenek. Elég bebizonyítani, hogy van 2n2/3 ember, akik együtt az összes többit ismerik, hiszen ezeknek egy-egy ismerősét hozzájuk véve együtt már mindenkit ismerni fognak. Hogy ne kelljen sokat egész részekkel számolni, csak azt az esetet mutatjuk be, amikor n köbszám.
Ha van valaki, aki legfeljebb 2n2/3 embert ismer, akkor kész vagyunk: az ismerősei együtt mindenki mást ismernek, ez 2n2/3 ember. Ha viszont bármely ember több, mint 2n2/3 másikat ismer, akkor bárhogyan választunk ki n2/3 embert, van köztük n1/3, akiknek van közös ismerősük (hiszen együttesen – multiplicitással számolva – 2n4/3 ismerősük van, tehát legalább egy olyan ember van, aki legalább n1/3-szor ismétlődik). Ezt addig csinálhatjuk, amíg van legalább n2/3 ember, akiket még nem vettünk tekintetbe. Vagyis n– n2/3 embert n1/3-os csoportokba állíthatunk úgy, hogy egy-egy csoportnak legyen közös ismerőse, ez lényegében n2/3 ember, a maradó (kevesebb, mint) n2/3 embert pedig hozzávesszük, így (kevesebb, mint) 2n2/3 embert kapunk, akik együtt az összes többit ismerik. Ezzel a bizonyítást befejeztük.
Megmutatjuk, hogy cn1/2-nél kevesebbre nem igaz az állítás.
Vegyünk ugyanis egy m pontú teljes gráfot, Km-et és csináljunk ebből egy G gráfot a következő módon. A G gráf csúcsai legyenek az n pontú teljes gráf élei, ez n=m(m–1)/2 pont. A G gráfban két pontot akkor kötünk össze, ha a megfelelő éleknek Km-ben van közös csúcsuk. A G gráfban bármely két pontnak van közös szomszédja (és G minden pontja 2m–4-ed fokú, ami nagyságrendileg 2n1/2).
Igaz a következő: akárhogyan választunk ki (m–1)/2-nél kevesebb élt a Km teljes gráfban, van olyan él, amellyel egyiknek sincs közös végpontja, vagyis az új gráfban akárhogyan választunk ki (m–1)/2-nél kevesebb pontot, van olyan pont, amellyel egyikük sincs összekötve. (m–1)/2 lényegében (n/2)1/2, biztos nagyobb, mint (n/2)1/2–1.
27.
A) Ellenpélda a „csillag”:
B) Ellenpélda: veszek két pontot, egymással nem kötöm össze őket, a gráf minden más pontjával összekötöm őket. (Ez a 2+(
n–2)-es teljes páros gráf, lásd a
II. fejezet 40. feladatának megoldása utáni megjegyzést.)
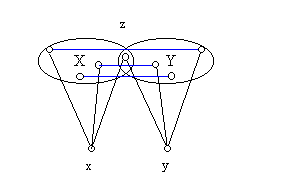
C) viszont igaz: ha egy gráfban nincs telített pont, bármely két össze nem kötött pontnak pontosan egy közös szomszéda van, összekötött pontoknak nincs közös szomszédjuk, akkor a gráf reguláris. Most ezt fogjuk bebizonyítani.
Először azt bizonyítjuk, hogy ha két pont nincs összekötve, akkor azonos a fokszámuk.
Legyen
x és
y két össze nem kötött pont a gráfban,
X és
Y legyen
x illetve
y szomszédainak halmaza. A feltétel szerint
X-nek és
Y-nak pontosan egy közös pontja van és
X-ben,
Y-ban nem fut él. Legyen
z a közös pont és legyen
u X egy tetszőleges,
z-től különböző pontja.
A feltétel szerint
u-nak és
y-nak pontosan egy közös szomszédja van, tehát
u Y-nak pontosan egy pontjával van összekötve és ez a pont nem lehet
z (mert
X pontjai között nem fut él). Ugyanígy látható be, hogy
Y minden,
z-től különböző pontja
X-nek pontosan egy pontjával van összekötve és ez a pont nem lehet
z. Ez azt jelenti, hogy
X\{
z} és
Y\{
z} pontjai között a gráf élei egy „matching”-et (egy-egyértelmű megfeleltetést, 1-faktort) alkotnak. Vagyis e két halmaz egyenlő elemszámú. Ezzel beláttuk, hogy
x és
y foka azonos. Tehát bármely két össze nem kötött pont foka azonos. Ha viszont
x és
y össze van kötve éllel, akkor van olyan
z pont, amellyel egyik sincs összekötve, s ezzel mindkettőnek azonos a foka. Ezzel beláttuk, hogy bármely két pont foka azonos, tehát a gráf reguláris.
HOL A HIBA az elmondott bizonyításban? Hol használtuk ki, hogy nincs a gráfban telített pont?
A hiba ott van, hogy feltettük, hogy ha
x és
y között fut él, akkor van olyan pont, amellyel egyikük sincs összekötve. Ez nem biztos, és nincs is rá szükségünk. Most megmutatjuk, hogy lehet jól befejezni ezt a bizonyítást.
Tekintsünk két olyan pontot, amelyek között fut él a gráfban, legyenek ezek
x és
y. Legyen
X x-nek
y-tól különböző szomszédai halmaza. Hasonlóan definiáljuk
Y-t is. A feladat feltétele szerint e két halmaz diszjunkt és egyiken belül sem fut él.
X pontjai nincsenek összekötve
y-nal, tehát a már bizonyítottak szerint mindegyikük foka megegyezik
y fokszámával. Ugyanígy
Y pontjainak fokszáma megegyezik
x fokszámával:
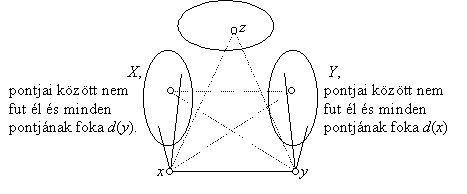
Ha van olyan
z pont, amely nincs benne a két halmaz egyesítésében és különbözik
x-től és
y-tól, akkor a már bizonyítottak szerint
z fokszáma egyezik
x fokszámával is,
y-éval is, tehát
x és
y fokszáma egyenlő. A továbbiakban feltehetjük, hogy nincs ilyen
z, azaz
XÈYÈ{
x,
y} tartalmazza a gráf összes pontját.
Ha van olyan
u pont
X-ben és
v pont
Y-ban, amelyek között nem fut él, akkor e két pont fokszáma is megegyezik, s ebből már következik, hogy a gráf összes pontjának azonos a fokszáma. Marad az az eset, ha
X és
Y pontjai között minden él be van húzva:
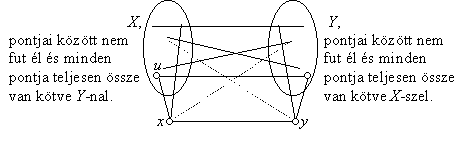
Ez azt jelenti, hogy
XÈ{
y} és
YÈ{
x} „teljes páros gráf”: azonos halmazbeli pontok között nem fut él, a két halmaz pontjai között viszont minden él be van húzva. Tegyük fel, hogy
X nem üres és legyen
u egy pontja. A feladat másik feltétele szerint
u-nak és
y-nak pontosan egy közös szomszédja van. Tudjuk, hogy
x közös szomszédjuk, tehát nincs több közös szomszédjuk. Márpedig
Y minden pontja közös szomszédjuk. Ebből következik, hogy
Y üres halmaz. De akkor
x telített pont, amit a feladat feltétele kizárt. (Itt használjuk ki azt a feltételt, hogy nincs telített pont.)
Ezzel bebizonyítottuk az állítást.
MEGJEGYEZZÜK, hogy már tudjuk, hogy bármely két össze nem kötött pont foka egyezik, akkor a bizonyítás talán valamivel egyszerűbben is befejezhető. Ehhez azonban használni kell az
összefüggő komponens fogalmát a következő fejezetből: Nyilván elég azt bizonyítani, hogy a komplementer összefüggő. Ez ugyanis pontosan azt jelenti, hogy tetszőleges
x és
y ponthoz vannnak olyan
v1v2…
vj pontok, amelyek közül
v1 x-szel,
vj y-nal nincs összekötve, és
vi nincs összekötve
vi+1-gyel. De akkor
x foka megegyezik
v1 fokával, az
v2-jével, az
v3-éval, stb. végül
vj-éval, s az
y fokával.
Tegyük fel, hogy a komplementer nem összefüggő, tehát a gráf pontjai két nem üres diszjunkt részhalmazra bonthatók, amelyek között a komplementerben nem megy él. Ekkor a két ponthalmaz közötti minden él a gráfban fut. Ha mindkét halmaz legalább kételemű, akkor bármely két pontnak, amely ugyanabban a halmazban van, legalább két közös szomszédja van a gráfban (hiszen a másik halmaz bármely pontja közös szomszéd). Ez azonban ellentmond a feladat feltételének. Tehát legalább az egyik halmaz egyelemű. Ekkor viszont ez a pont az összes többivel össze van kötve, amit szintén kizártunk.
D) igaz. Átfogalmazzuk a feladatot gráf-nyelvre: azt állítjuk, hogy ha egy véges egyszerű gráfban bármely két pontnak ugyanannyi közös szomszédja van, akkor a gráf vagy reguláris, vagy van benne telített pont.
Legyen
x a gráf egy tetszőleges pontja, legyen a fokszáma
d és legyenek a szomszédai
x1,
x2,…,
xd. Először megállapítjuk, hogy minden
xi-nek pontosan egy szomszédja van az
xj-k között. Ez abból következik, hogy
xi-nek és
x-nek pontosan egy közös szomszédja van. Ha a gráfnak nincsenek további pontjai, akkor kész vagyunk. Ha vannak, akkor legyen
Ai azoknak a pontoknak a halmaza, amelyek szomszédjai
xi-nek, és különböznek
x-től is,
xj-ktől is. Ha
i és
j különböző, akkor
Ai és
Aj diszjunkt (különben
xi-nek és
xj-nek két közös szomszédja volna). Ha
xi és
xj között nem fut él, akkor
Ai egy tetszőleges
y pontjának és
xj-nek csak
Aj-ben lehet közös szomszédja (hiszen
xj-nek szomszédja
Aj-n kívül csak
x és egy –
xi-től feltevésünk szerint különböző –
xk lehet). Másrészt
y nem lehet két
Aj-belivel összekötve, mert ekkor
y-nak és
xj-nek két közös szomszédja is volna. Tehát minden
yÎAi pontosan egy
Aj-belivel van összekötve, ha
xixj nem éle a gráfnak. Természetesen ugyanez igaz
i és
j felcserélésével is, amiből viszont következik, hogy ha
xixj nem éle a gráfnak, akkor |
Ai|=|
Aj|.
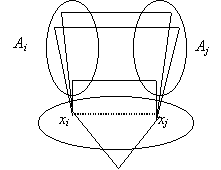
Ha viszont
xixj éle a gráfnak akkor
yÎAi és
zÎAj között nem mehet él, mert ezesetben
xiyzxjxi négyszög volna a gráfban, amit a feladat feltétele kizár. Végül ugyanígy látható be az is, hogy
yÎAi pontosan egy
zÎAi-beli ponttal van összekötve. Ebből viszont következik, hogy
d(
y)=1+
d–1 (szomszédai:
xi, egy kivétellel minden
Aj-ben egy pont, –
Ai-ból is egy!). Tehát
d minden olyan pont foka, amely valamelyik
Ai-ben van. Mivel minden
x-szel össze nem kötött pont benne van valamelyik
Ai-ben, ezért minden olyan pont foka
d, amely nincs összekötve
x-szel.
Ezzel azt is beláttuk, hogy bármely két össze nem kötött pont foka azonos. Be akarjuk látni, hogy ha sem
x, sem szomszédai (tehát az
xi-k)
nem telített pontok, akkor szomszédainak is
d a foka.
Ha
x nem telített pont, akkor van olyan
Ai, amely nem üres. Ennek minden pontja
d-ed fokú. Másrészt nincs olyan
xi-től különböző
xj, amellyel valamely
Ai-beli pont össze lenne kötve (különben
xi-nek és
xj-nek
x-en kívül is volna közös szomszédja). Tehát minden
xi-től különböző
xj foka is megegyezik az
Ai-beli pontok fokával,
d-vel. Ezzel beláttuk, hogy minden
xi-től különböző pont foka
d. Ha
xi nem telített pont, akkor van olyan pont, amellyel nincs összekötve, s ezzel megegyezik a foka, tehát
xi foka is
d.
Az állítás bizonyítását ezzel befejeztük.
Azt is meg tudjuk mondani, hogy ha nincs telített pont, akkor milyen összefüggés áll fenn
d és a pontszám között: minden
Ai elemszáma
d–2, tehát
n=1+
d+
d(
d–2)=
d2–
d+1. Ha
d–1=
p prím, akkor a
p2+
p+1 elemű véges geometriából lehet megfelelő gráfot csinálni: minden pontot a polárisának pontjaival kötünk össze (pontosan
p+1=
d ilyen pont van). Ismert, hogy ha egy
P pont rajta van
Q polárisán, akkor
Q is rajta van
P polárisán, tehát egyszerű (irányítatlan) gráfot kapunk.
P és
P’ közös szomszédja az a
Q pont, amely rajta van
P és
P’ polárisán, vagyis
Q a
PP’ egyenes pólusa. Ilyen
Q pedig pontosan egy van.
MEGJEGYZÉS:
A tétel speciális esete Erdős és De Bruijn nevezetes tételének, amely szerint egy n elemű halmaznak legfeljebb n részhalmaza adható meg úgy, hogy bármely kettőnek pontosan egy közös eleme legyen.
28.
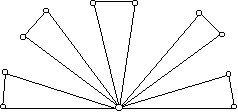
49 pontú gráf van ezzel a tulajdonsággal: legyen x telített pont, azaz legyen összekötve minden más ponttal. A többi 48 pontot osszuk 24 párba és fusson egy-egy él a az azonos párba tartozó pontok között. (Ezt a gráfot megkaphatjuk úgy is, hogy 24 háromszöget illesztünk úgy össze, hogy egy csúcs mind a 24-ben közös legyen.) Ekkor bármely két ponthoz pontosan egy olyan pont van, amely mindkettőnek szomszédja. Hasonló konstrukció (n háromszög összeillesztésével) minden n-re ad egy 2n+1 pontú megfelelő gráfot. (Az ábra sematikus, öt háromszöget rajzoltunk ki az n-ből.)
Megmutatjuk, hogy páros pontszám esetén nincs ilyen gráf.
1. MEGOLDÁS:
Ha egy G gráfnak megvan az a tulajdonsága, hogy minden pontpárnak páratlan sok közös szomszédja van, akkor a gráfban minden pont foka páros. Legyen ugyanis x egy pont, V a szomszédainak halmaza. Ha yÎV, akkor y pontosan azokkal a pontokkal van összekötve V-ből, amelyek közös szomszédai x-nek és y-nak, s ezek száma páratlan. A V által feszített részgráfban tehát minden pont foka páratlan. Ebből viszont a 20. feladat szerint következik , hogy V-nek páros sok pontja van.
Legyen most x és y két tetszőleges pontja G-nek, legyen Vxy a közös szomszédaik halmaza, Vx x azon szomszédainak halmaza, amelyek nincsenek összekötve y-nal, Vy pedig y azon szomszédainak halmaza, amelyek nincsenek összekötve x-szel. A feltétel szerint |Vxy| páratlan, és láttuk, hogy x és y fokszáma, azaz |Vxy|+|Vx| és |Vxy|+|Vy| páros, tehát |Vx| és |Vy| is páratlan. Vx, Vy, Vxy páronként diszjunkt, tehát VxÈVyÈVxy elemszáma páratlan.
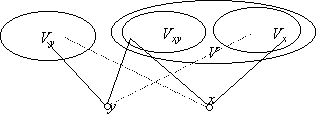
Minthogy a gráf pontszáma páros, a kimaradó pontok száma is páratlan, s ezek éppen azok a pontok, amelyek sem x-szel, sem y-nal nincsenek összekötve. Megjegyezzük, hogy ha x és y össze van kötve G-ben, akkor x benne van Vy-ban és y benne van Vx-ben, ekkor VxÈVyÈVxy tartalmazza mindkettőt. Ha viszont x és y nincs összekötve, akkor egyiket sem tartalmazza (az ábra az utóbbi esetet mutatja). Mindkét esetben azt kapjuk, hogy páratlan azoknak a pontoknak a száma, amelyekkel sem x, sem y nincs összekötve és különböznek mindkettőtől. Vagyis: G komplementer gráfjának is megvan az a tulajdonsága, hogy bármely két pontjának páratlan sok közös szomszédja van.
De akkor a komplementer gráfban is páros minden pont foka. Márpedig páros pontszámú gráfnál minden pont foka vagy a gráfban vagy komplementerében páratlan (lásd a 8. feladatot). Tehát a feladat feltételének csak olyan gráf felelhet meg, amelyben a pontok száma páratlan.
II. MEGOLDÁS:
Ha már tudjuk, hogy a gráfban minden pont foka páros, a bizonyítást gyorsabban is befejezhetjük: vegyünk egy x pontot, legyen ezek szomszédainak halmaza X. A kimaradó pontok száma páratlan, ezért az általuk feszített részgráfban van páros fokú pont, legyen ez y. Minthogy y gráfbeli foka is páros, ezért X-ből páros sok ponttal van összekötve (x-szel nincs összekötve), tehát x és y közös szomszédainak száma páros.
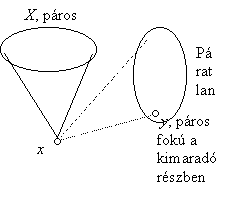
Ez az ellentmondás bizonyítja eredeti állításunkat.
29.
A feladatot gráfelméleti nyelven elmondva azt kell belátnunk, hogy ha egy n pontú gráfban nincs háromszög (vagyis három olyan pont, amelyek közül bármely kettő össze lenne kötve) és nincs üres hétpontú gráf, akkor legfeljebb 3n éle van. Ennél több is igaz: igaz az, hogy minden pont foka legfeljebb hat. Ez azért igaz, mert ha egy gráfban nincs háromszög, akkor bármely pont szomszédai üres gráfot alkotnak. (Az ábrán szaggatott vonal jelzi a nem-éleket.)
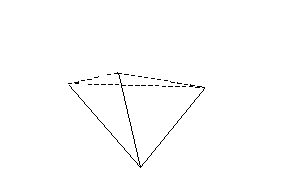
Tehát a mi gráfunkban bármely pontnak legfeljebb hat szomszédja lehet. Ebből viszont már következik a feladat állítása: a 12. feladatban láttuk, hogy az élszám éppen a fokszámok összegének a fele. Esetünkben a fokszám összeg legfeljebb 6n, tehát az élszám legfeljebb 3n.
30.
Tegyük fel, hogy nem. Ekkor van egy V1 versenyző, aki legfeljebb 15 másikkal játszott, különben az összes versenyző halmaza megfelel. Legyen az összes versenyző halmaza H és tekintsük a H1=H–V1 halmazt. Ha ez nem megfelelő, akkor van egy olyan V2 versenyző benne, aki a H1 tagjai közül legfeljebb 15-tel mérkőzött. Tegyük fel, hogy a V1, V2, …, Vk versenyzőkről már tudjuk, hogy közülük Vi a H–{V1,V2,…,Vi–1} halmazba tartozó versenyzők közül legfeljebb 15-tel játszott. Tekintsük a H–{V1,V2,…,Vk} halmazt. Ha ez sem megfelelő, akkor itt is van egy Vk+1 versenyző, aki a halmazban szereplő többi versenyző közül legfeljebb 15-tel játszott. Így végül azt kapjuk, hogy a versenyzők sorozatba rendezhetők úgy, hogy mindenki legfeljebb 15-tel játszott azok közül, akik a sorozatban később következnek. Az utolsó 15 emberről ráaadásul az is nyilvánvaló, hogy kevesebb, mint 15-tel játszottak, hiszen utánuk már csak kevesebb, mint 15-en vannak. De ez azt jelenti, hogy az összes lejátszott mérkőzés száma kevesebb, mint 15n, hol n az összes versenyző száma. Ezesetben viszont a versenyzők átlagosan kevesebb mint 30 mérkőzést játszhattak (lásd a 12. feladatot). A pontos állítás tehát a következő:
Ha egy gráfban az átlag fokszám legalább 2k, akkor van olyan feszített részgráfja, amelyben minden pont foka legalább k+1.
31.
a) „Felépítjük” a gráfot. Egy ilyen gráf bármely feszített részgráfjára is igaz, hogy bármely öt pontja közt legalább két él fut, tehát ún. örökletes tulajdonságról van szó, ezért alkalmazható lesz a teljes indukció.
Egy ötpontú megfelelő gráf élszáma legalább 2, hiszen épp ez a feladat feltétele.
Egy hatpontú megfelelő gráf élszáma legalább három, és három él csak akkor elég, ha a három élből semelyik kettőnek nincs közös végpontja.
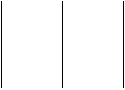
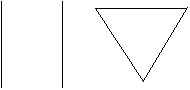
Egy hétpontú megfelelő gráfban már van másodfokú pont. Ha ugyanis minden pont foka legfeljebb 1 volna, akkor csak három él lehetne a gráfban, s ezek közül kettőnek egy-egy végpontját elhagyva olyan öt pont maradna, amelyek közt csak egy él fut. Tehát van egy másodfokú pont. Hagyjuk el ezt, a maradó hat pontú gráfnak legalább három éle van, így az eredeti gráfnak legalább öt éle van. Ha egy gráf két pontfüggetlen élből és egy ezektől pontdiszjunkt háromszögből áll, ez pont megfelelő gráf, és valóban öt éle van. Könnyen belátható, hogy ez az egyetlen jó példa öt élű, hétpontú megfelelő gráfra.
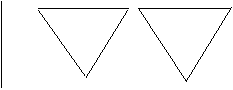
Egy nyolcpontú megfelelő gráfban is van legalább egy legalább másodfokú pont (hiszen bármely hétpontú részgráfjában is van), ezt elhagyva a maradó hétpontú gráfnak legalább öt éle van, ami összesen legalább hét él. Két pontfüggetlen háromszögből és egy tőlük független élből álló nyolcpontú gráf olyan hét élű, nyolcpontú gráf, amely megfelel. (Könnyű látni, hogy több példa nincs is.)
Hasonlóan kapjuk, hogy egy kilencpontú megfelelő gráfban is van legalább egy másodfokú pont, ezt elhagyva a maradó gráf legalább hét élű, így összesen legalább kilenc éle van egy megfelelő kilencpontú gráfnak. Három páronként pontfüggetlen háromszög mutatja, hogy kilenc élű megfelelő gráf van is. Itt is könnyen belátható, hogy ez az egyetlen kilencélű példa.
A tízpontú gráf esetén már azt kell megmutatnunk, hogy van egy legalább harmadfokú pont. Az biztos, hogy van legalább másodfokú pontja, ezt elhagyva a maradó kilenc pontú gráfban legalább kilenc él van, összesen tehát legalább tizenegy éle van a gráfnak. De ha minden pont foka legfeljebb kettő volna, akkor a gráf élszáma az élszámra vonatkozó
Euler-tétel szerint nem lehetne több tíznél. Tehát van legalább harmadfokú pont a gráfban. Ezt elhagyva a maradó kilencpontú gráfban legalább kilenc él van, ez összesen legalább 12 él. Két pontfüggetlen háromszögből és egy tőlük pontfüggetlen teljes négyesből álló gráf megfelelő, és 12 éle van.
b) Általában azt állítjuk, hogy egy megfelelő, legalább 3k+1 pontú gráfban van legalább k-adfokú pont.
Ezt k³3-ra a következőképpen bizonyíthatjuk: Ha egy megfelelő, 3k+1 pontú gráfban minden pont foka legfeljebb k–1, akkor kiválasztható négy pont, amelyek közt nem fut él (lásd az előző feladatot: az első pontot tetszőlegesen választjuk, elhagyjuk a szomszédait, a maradó legfeljebb 2k+1 pontból kiválasztunk egyet tetszőlegesen, elhagyjuk szomszédait, a maradó k+1 pontból megint választunk egyet, elhagyjuk szomszédait, és még mindig marad egy pont, amely a kiválasztott háromtól független.) Mivel a gráf megfelelő, az összes többi pontjából megy legalább két él e négy ponthoz. E négy pontba tehát összesen legalább 2(3k–3) ³ 4k él fut, s így legalább az egyikük fokszáma legalább k, ami ellentmondás. Tehát valóban van benne k-adfokú pont.
Ha már tudjuk, hogy egy legalább 3k+1 pontú megfelelő gráfban van legalább k-adfokú pont, akkor teljes indukcióval könnyű belátni, hogy n=3k esetén egy megfelelő gráf minimális élszáma 3k(k–1)/2, n=3k+1 esetén ennél k-val több, n=3k+2 esetén pedig még k-val több. n=3-ra igaz az állítás (l. a)-t). Tegyük fel, hogy n=3k-ra igaz az állítás, és tekintsünk egy megfelelő 3k+1 pontú gráfot. Az előbb bizonyítottak szerint ebben van legalább k-adfokú pont. Hagyjuk el. A maradó 3k pontú megfelelő gráf élszáma legalább 3k(k–1)/2, s ehhez visszatéve az elhagyott pontot azt kapjuk, hogy az eredeti gráf élszáma legalább 3k(k–1)/2 + k, ahogy állítottuk. n=3k+2-re ugyanígy megy az indukció, és n=3k+3-ra is, utóbbi esetben azt kapjuk, hogy a minimális élszám 3k(k–1)/2 + 3k = 3k(k+1)/2, tehát visszajutottunk az indukciós feltevéshez eggyel nagyobb k-ra.
Ezzel beláttuk, hogy egy megfelelő gráf minimális élszáma 3k(k–1)/2 + ik, ahol n=3k+i alakú (i=0,1 vagy 2). Végül meg kell még mutatnunk, hogy ilyen élszámú megfelelő gráf van is. A fenti bizonyítást végiggondolva azt kapjuk, hogy az egyetlen minimális élszámú megfelelő gráf az, amelyben a pontokat három, lehetőleg egyenletes osztályba soroljuk, s egy osztályon belül az összes élt behúzzuk, különböző osztályok közt nem húzunk be élt.
MEGJEGYZÉS:
Erdős Páltól származik az általános kérdés, hogy minimálisan hány éle van egy olyan n pontú gráfnak, amelynek bármely s pontja között legalább két él fut? Az általános kérdésre a fentihez hasonló módon adható válasz, erre majd a Turán-típusú tételekről szóló fejezetben térünk vissza.
32.
Írjunk minden élre egy-egy prímszámot, különböző élekre különbözőt. (Végtelen sok prím van, tehát ez lehetséges.) Majd minden csúcsra írjuk a belőle induló éleken szereplő számok szorzatát. Ekkor két csúcson szereplő számnak pontosan akkor van egynél nagyobb közös többszöröse, ha él köti össze őket. Az első feladat tehát minden egyszerű poliéderre megoldható. Sőt: minden véges gráfra is. Ebből viszont következik, hogy a második feladat is megoldható: a poliéderhez azt a gráfot rendeljük, amelyben két csúcsot pontosan akkor köt össze él, ha a poliéderben nem szomszédosak.
33.
A tetraéder esetén minden csúcsra ugyanaz a szám kerül másodszor, mint ami először volt rajta, itt tehát annyi páratlan számot kapunk a második menetben, ahányat eredetileg a csúcsokra írtunk. Vagyis 0 és 4 között bárhány páratlan számot kaphatunk. Az oktaéder esetében a második menetben minden csúcsra a rajta és a vele szemben álló szám összegét írjuk. Ebből következik, hogy egy csúcsra és a vele szemben levőre ugyanaz a szám kerül. Az oktaédernek hat csúcsa van, tehát három különböző összeg kerül a hat csúcsra, ezek között viszont bárhány lehet páratlan: ha azt akarjuk, hogy egy párra második menetben páratlan szám kerüljön, akkor az első lépésben az egyikre nullát, a másikra egyet írunk. Ha azt akarjuk, hogy páros szám kerüljön rájuk a második menetben, az első menetben mindkettőre nullát írunk. Itt tehát 0 és 3 között bárhány páratlan szám lehetséges.
A kocka esetében a nyolc csúcsból akárhányra kerülhet páratlan szám a második menetben. Ha mindegyikre nullát írunk az első menetben, akkor a második menetben mindegyikre páros szám (nulla) kerül. Ha mindegyikre egyet, akkor a második menetben mindegyikre 5 kerül, tehát páratlan. Általában igaz az, hogy ha az első menetben írt számok paritását megfordítjuk (például mindegyikhez hozzáadunk egyet), akkor a második menetben írt számok paritása is megfordul, hiszen a második menetben öt csúcson álló számot kell összeadnunk. (Ez minden olyan gráfra igaz, amelyben minden pont „nem-foka”, azaz komplementerbeli foka páratlan, így az ikozaéder gráfjára is.) Elég tehát azt megmutatnunk, hogy lehet 8,7,6,5 vagy 4 páratlan szám a második menetben, mert ekkor lehet ugyanennyi páros is, ami rendre 0,1,2,3 vagy 4 páratlan számot jelent. Láttuk már, hogy 8 db páratlan szám előállítható. Hét páratlan számot kapunk, ha egy x csúcsra, x szomszédaira és a vele átellenesre egyet írunk, a három további csúcsra pedig nullát. Ekkor az x csúcson a második menetben kettő fog állni, minden más csúcson páratlan szám. Most ugyanis S=5, és minden más csúcs páros sok olyan csúccsal van összekötve, amelyre egyet írtunk. Hat páratlan számot kapunk a második menetben, ha egy csúcsra és a vele átellenesre egyet írunk, a többire nullát. Ekkor ugyanis e két csúcson kettő fog állni a második menetben, minden további csúcs pedig pontosan egyikükkel van összekötve, tehát a többi hat csúcson egy fog állni. Írjunk két szomszédos csúcsra, x-re és y-ra, valamint az x-szel átellenes z csúcsra egyet, a többire nullát. Ekkor x-re, y-ra a második menetben kettő kerül, szintén kettő kerül x-nek y-tól különböző két szomszédjára, y és z két közös szomszédjára egy kerül, z-nek a maradó harmadik szomszédjára is kettő kerül, végül magára z-re három, tehát három páratlan számot kapunk a második menetben. A „komplementer” elrendezés adja az 5 páratlan számot. Végül négy páratlan számot a második menetben úgy kaphatunk, ha az első menetben egy x csúcs három szomszédjára írunk egyet, mindenüvé máshová nullát. Ekkor x-re nulla kerül a második menetben, az x-szel ellentétes z csúcsra három, z szomszédaira kettő (mindegyiknek pontosan egy közös szomszédja van x-szel), x szomszédaira pedig három.
A 12 csúcsú ikozaéder esetében is kaphatunk bárhány páratlan számot a második menetben 0 és 12 között. Az előző megjegyzés szerint elég azt megmutatni, hogy 0,1,2,3,4,5 vagy 6 páros számot kaphatunk. 0 db páros számot kapunk (a második menetben), ha minden csúcsra nullát írunk. Legyen A és D az ikozaéder két „átellenes pontja”, A szomszédai legyenek B1B2B3B4B5 (ahol Bi és Bi+1 szomszédosak, az indexelés mod 5 megy), D szomszédai legyenek C1C2C3C4C5 (ahol Ci és Ci+1 szomszédosak, az indexelés itt is mod 5 megy), és Bi szomszédai még Ci és Ci+1. Írjunk nullát A-ra és minden Bi-re, továbbá D-re, és írjunk egyet minden Ci-re. Ekkor a második menetben A-ra öt kerül, minden Bi-re és minden Ci-re kettő, D-re pedig nulla. Most tehát pontosan egy csúcson lesz páratlan szám. Két páratlan számot akkor kapunk, ha A-ra és D-re nullát írunk, minden más csúcsra egyet. Ekkor A-n és D-n a második menetben öt lesz, a többi csúcson hat. Ha A-ra, B1-re és B2-re nullát írunk, a többi csúcsra egyet, akkor a második menetben három páratlan csúcsot kapunk: C1, C3 és B4 lesz páratlan. Ha a Bi csúcsokra írunk 1-et, a többi hét csúcsra nullát, akkor az A csúcsra nulla kerül, D-re páratlan szám (5), minden további csúcsra három kerül, tehát pontosan egy csúcson lesz páros. Ha az eredeti számozásban a 0-k és 1-esek helyét megfordítjuk, akkor pontosan egy páratlan számot kapunk a „második fordulóban”.
Ez utóbbiból kapható rögtön egy általános megoldás is, ha tetszőlegesen megjelölünk k csúcsot, akkor elérhető, hogy pontosan ezeken a csúcsokon legyen a „második fordulóban” páratlan szám. Ehhez csak annyit kell észrevennünk, hogy ha két „első forduló” számait összeadjuk minden csúcson, akkor a „második fordulóbeli” csúcsok is összeadódnak. Ha tehát kijelölünk k darab csúcsot, akkor a következő k darab számozást adjuk össze: kiválasztjuk az egyik kijelölt csúcsot és szomszédaira nullát írunk, a másik hét számra pedig egyest. Ezután ezt a k darab számozást összeadjuk. Kész.
34.
Kiválasztunk egy maximális fokszámú embert, A-t, (egy ember foka=az általa ismert emberek száma), és egy B-t, akit nem ismer. Ha van olyan C, akit B ismer, de A nem, akkor – mivel B foka nem nagyobb A fokánál –, van olyan D is, akit A ismer, de B nem. Ezek négyen jók.
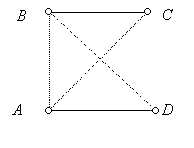
Ha
A ismeri
B minden ismerősét, akkor legyen
C egy közös ismerősük. Van olyan
D ismerőse is
A-nak, akit
C nem ismer, különben
C ismerné
A összes többi ismerősét plusz
A-t és
B-t, tehát magasabb volna a foka
A fokánál.
A,
B,
C,
D megint jó. (Hol használtuk ki, hogy izolált ember sincs?)
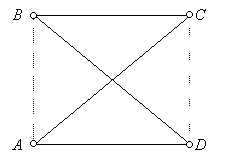
35.
Tekintsük azt a gráfot, amely a barátságokat ábrázolja. Egy törpe pontosan akkor festi át a házát, ha így több barátjával lesz azonos színű a háza, vagyis ha az azonos színű pontokat összekötő élek száma nő a gráfban. Mivel az élek az évek során nem változnak és számuk véges, ezért legkésőbb annyi év múlva, ahány barátság van köztük (ahány él van a gráfban), a törpéknek nem lesz miért átfesteni házikójukat.
36.
Legyen A és B tagszáma n. Tekintsük A összes nem üres részhalmazát, ezek száma 2n–1. Minden ilyen részhalmazhoz rendeljünk hozzá egy n hosszú 0-1 sorozatot: ennek i-edik eleme 0, ha B delegáció i-edik tagja a részhalmazból páros sokat ismer és 1, ha páratlan sokat. A kapott n hosszú 0-1 sorozatok közt vagy előfordul a csupa 0, csupa 1 egyike, s ekkor kész vagyunk, vagy van két egyforma. Legyen a két részhalmaz C és D. Vegyük C és D szimmetrikus differenciáját, ez legyen E. Ha B delegáció i-edik tagja C-ből c(i), D-ből d(i) embert ismer, s ebből f(i) van C és D közös részében, akkor E-ből c(i)+d(i)–2f(i) embert ismer. Mivel c(i) és d(i) paritása ugyanaz (C-hez és D-hez ugyanaz a sorozat tartozik), ezért E-ből B delegáció i-edik tagja páros sok embert ismer. Ez minden i-re igaz és E nem üres (C és D különböző), tehát kész vagyunk.
37.
A gráf pontjai szerinti teljes indukciót alkalmazunk. Ha minden pont foka páros, akkor nincs mit bizonyítanunk. Ha van egy x páratlan fokú pont, akkor legyen S a szomszédainak halmaza, T a többi pont. Vegyük az S által feszített gráf komplementerét, és vegyük hozzá az ST és a TT éleket.
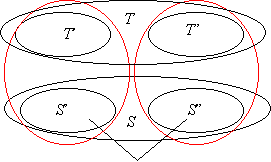
Az így kapott
G’ gráfra alkalmazzuk az indukciós feltételt: két részre bontható
S=S’+S” és
T=T’+T” úgy, hogy az
S’ÈT’ és az
S”
ÈT” által
G’-ben feszített részgráfokban minden pont foka páros.
S’ és
S” közül az egyik páratlan sok pontból áll, mondjuk
S’. Ekkor
S” páros sok pontból áll. Cseréljük most vissza
S’-ben és
S”-ben az éleket az eredeti élekre és tegyük hozzá
x-et
S’-höz. Ekkor
S”-ben marad minden fok paritása, és
S’-ben minden fok paritása megfordulna, de hozzávettük
x-et, amellyel mind össze van kötve. Ezzel a bizonyítást befejeztük.
38.
Megjegyezzük, hogy a feladat feltételéből következik, hogy mindenki mindenkivel csak egyféle játékot játszik. Három embert összesen (3n+1)n(3n–1)/2 féleképpen tudunk kiválasztani. Számoljuk össze, hány olyan hármas van ezek között, amelynek tagjai csak egy vagy kétféle játékot játszanak egymás között. A társaság egy A tagja n emberrel pingpongozik, tehát n(n–1)/2 olyan hármasban van benne, amelynek két tagjával pingpongozik. Ugyanennyi olyan hármasban van benne, amelynek két tagjával teniszezik és ugyanennyi hármas van, amelynek két tagjával sakkozik. Ő tehát 3n(n–1)/2 hármast „ront el”. Az olyan társaságok száma tehát, amelyekben valaki két partnerével ugyanolyan játékot játszik, legfeljebb 3n(n–1)(3n+1)/2. (Azért legfeljebb, mert az olyan hármasokat, amelyben mindenki ugyanazt a játékot játssza két partnerével, háromszor számoltuk.) Az olyan hármasok száma tehát, amelyben mind a három játékot játsszák, legalább
(3n+1)n(3n–1)/2 – 3n(n–1)(3n+1)/2 = (3n+1)n > 0.
Ezzel a feladat állítását bebizonyítottuk. Rögtön egy aránylag nagy alsó becslést is adtunk a megfelelő hármasok számára. Azonban ez az összes szóba jövő hármasnak még csak olyan kis hányada, amely a nullához tart, ha n tart a végtelenbe. Megmutatható, hogy az összes hármasoknak legalább az 1/16-a megfelelő, másrészt 1/6-nál nagyobb része nem mindig megfelelő. (Lásd: Surányi László: Megjegyzések az 1987. évi Kürschák József matematikai tanulóverseny 3. feladatához. KöMaL 38(1988) 337–346.)
A feladat állítására még több szép bizonyítás adható, ezeket lásd Surányi János: Matematikai versenytételek III. rész Tankönyvkiadó 333-337.
39.
Ezt a feladatot a „vegyük a legnagyobbat” módszerrel lehet megoldani: Vegyünk egy olyan tanulót, aki a legtöbb tanulót ismeri a másik két iskola egyikéből. Nevezzük őt A-nak és az iskoláját az első iskolának, azt az iskolát, ahonnan sok tanulót ismer, a második iskolának, a maradót a harmadik iskolának. Ismerjen k tanulót a második iskolából. Ekkor a harmadik iskolából legalább n+1–k tanulót ismer. Vegyünk közülük egyet (ilyen van, mert n+1–k > 0), nevezzük B-nek. Ha B ismer a második iskolából valakit, akit A is ismer, akkor megtaláltuk a három megfelelő tanulót. Ha nem, akkor B a második iskolából legfeljebb n–k tanulót ismer, így az első iskolából legalább n+1–(n–k) = k+1 tanulót ismer. De akkor találtunk valakit: B-t, aki egy másik iskolából több, mint k tanulót ismer és ez ellentmondás.
40.
Legyen a j-edik csúcs fokszáma dj.
Tekintsük az első i csúcs halmazát, legyen ez H, és legyen a többi csúcs halmaza L.
Becsülni fogjuk a H és L halmaz között futó élek számát, jelöljük ezt EH,L-lel. Ezek száma legfeljebb annyi, ahány él az L halmaz csúcsaiból kiindul, tehát legfeljebb
EH,L £ di+1+di+2+…+dn.
Másrészt a H halmazból legalább d1+d2+…+di–i(i–1)/2 él indul az L halmazba, hiszen az egyes csúcsokból kiinduló élek száma d1+d2+…+di, és a H halmazon belül futó élek száma legfeljebb i(i–1)/2, az összes további él egy H és egy L-beli pontot köt össze. (Éppen ezért ezek mindegyikét csak egyszer számoljuk.) Tehát
EH,L ³ d1+d2+…+di–i(i–1)/2.
Az EH,L-ra kapott két becslést összevetve éppen a kívánt állítást kapjuk:
di+1+di+2+…+dn ³ d1+d2+…+di–i(i–1)/2.
41.
a) Az egypontú gráf pontja telített pont is, izolált pont is. A kétpontú, élnélküli gráfban két izolált pont van, ha behúzzuk az élt, két telített pont lesz. A hárompontú gráfok közül az üres és az egyélű gráfban van izolált pont, a két- és háromélűben van telített (másodfokú) pont. A négypontú gráfok között már van olyan gráf, amelyben nincs sem telített, sem izolált pont: például az, amelyik két, közös pont nélküli élből áll.
b) Ha egy négypontú gráfban nincs sem telített pont, sem izolált pont, akkor minden pont foka egy vagy kettő. Három eset van:
– Minden pont foka egy, ami csak úgy lehet, ha két, közös pont nélküli élből áll a gráf. Ez három lehetőség:



– Minden pont foka kettő. Az ilyen gráfok komplementerében minden pont foka egy, tehát ilyenből is három van. Egyébként ezek a gráfok négy hosszú úgynevezett „
körök”, például az utolsó gráf komplementere ilyen:

– Két pont foka kettő, két pont foka egy (a gráf egy gráfelméleti „út”), a két első fokú pont egy-egy másodfokúval van összekötve és a két másodfokú egymással is össze van kötve:

A két elsőfokú pontot hatféleképpen választhatjuk, a maradó két pont sorrendjét pedig kétféleképpen, ez összesen 12 lehetőség.
Összesen tehát 3+3+12=18 olyan négypontú gráf van, amelyben nincs telített pont és nincs izolált pont sem.
c)
Egy gráfban nem lehet egyszerre telített és izolált pont. Ha egy gráfban van telített pont, akkor a komplementerében van izolált pont és fordítva. Ha egyik sincs a gráfban, akkor a komplementerében sincs egyik sem. Tehát a sem telített, sem izolált pontot nem tartalmazó gráfokat párba állíthatjuk: mindegyiknek a komplementere lesz a párja. Minthogy
n legalább 2,
a csúcsok számozottak, egyetlen gráfnak sem lehet önmaga a komplementere. Ezzel a feladat állítását beláttuk.
d)
Ha egy pont telített a gráfban, akkor a gráf komplementerében izolált pont. Ezért az izolált pontot tartalmazó gráfok száma is
Tn. Ezt fogjuk meghatározni. A logikai szitaformulát használjuk.
Rögzítsünk
k pontot a gráfban és tekintsük azokat a gráfokat, amelyekben ez a
k pont izolált pont. Nyilvánvalóan annyi ilyen gráf van, ahány gráf van a maradó
n–
k ponton:
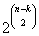
(lehetnek további izolált pontok is: ezért lesz szükség a logikai szitára). A
k pontot
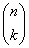
féleképpen választhatjuk ki. Ezért az izolált pontot tartalmazó gráfok száma a logikai szitaformula szerint:
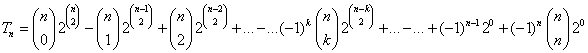
.
Itt az utolsó kettő kivételével minden tag páros. Az utolsó mindig páratlan (1), viszont az utolsó előtti paritása megegyezik
n paritásával. Így
Tn minden páros (pozitív egész)
n-re páratlan, minden pozitív páratlan
n-re páros.

























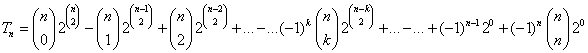 .
.