MEGOLDÁSOK:
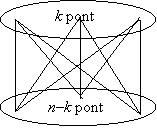
21. Ha a gráf nem összefüggő, akkor legalább két komponensből áll. Ha több mint két komponensből áll, akkor valamelyik két komponens között még húzhatunk be éleket, ezzel az élszámot növeljük és a gráf továbbra sem lesz összefüggő. Tehát a maximális élszámú nem összefüggő gráfban két komponens van. Ha ezek pontszáma k és n–k (feltesszük, hogy k≤n–k), akkor az élszám kétszeresének maximuma
k2 – k + (n–k)2 – n + k = n2 – n – 2k(n–k) ≤ n2 – 3n + 2.
Tehát a nem összefüggő n pontú gráf élszámának maximuma (n2 – 3n + 2)/2.
22. Azt kell belátnunk, hogy ha egy körből elhagyunk egy xy élt, akkor továbbra is bármely két pont között megy út. Az x és y között továbbra is megy út: ez éppen a kör megmaradt éleiből áll. Legyen tehát a és b a gráf két pontja. Elég belátni, hogy megy közöttük séta. Az eredeti gráfban ment közöttük út. Ha ez az út nem tartalmazta az xy élt, akkor továbbra is benne van a gráfban. Ha tartalmazta az xy élt, akkor helyettesítsük az élt azzal az xy-úttal, amely a kör megmaradt éleiből áll. Így egy sétát kapunk a két pont között, amely nem használja az xy élt, tehát továbbra is van séta a gráfban a és b között.
23. Ha a gráf körmentes volna, akkor legfeljebb n–1 éle lehetne. Tehát van benne kör. Ha ebből a körből elhagyunk egy élt, akkor a gráf továbbra is összefüggő (lásd az előző feladatot). Másrészt n–1 éle van, tehát fa. Az elhagyott él nélkül tehát nincs benne kör. Ebből következik, hogy minden körének éle az elhagyott él. Ha viszont lenne két különböző köre, akkor lenne olyan él is, amelyik ezek közül az egyikben nincs benne. De akkor elhagyhatjuk ezt az élt is, s akkor összefüggő n–1 élű gráfot kapnánk. De az ilyen gráf fa, tehát nem lehetne benne kör.
24. Azonos paritású színek pontjai között nem fut él, hiszen a fában minden él két szomszédos szintet köt össze egy éllel. Vagyis a gráf pontjait két osztályba sorolhatjuk úgy, hogy az azonos osztálybeli pontok független ponthalmazt alkotnak. (Ez csak más megfogalmazása annak, hogy minden fa páros gráf.) A két ponthalmaz egyike a gráf csúcsainak legalább a felét tartalmazza.
25. Ha az állítás nem volna igaz, akkor két útnak volna két közös pontja, amelyeket két különböző út kötne össze, és ez (C) szerint lehetetlen.
26. Tegyük fel, hogy van két leghosszabb út, U1=P1P2…Pk és U2=Q1Q2…Qk, amelyeknek nincs közös pontjuk. A gráf összefüggő, tehát van olyan út, amely a két út egy-egy pontját köti össze. Nyilván feltehetjük azt is, hogy ez az út nem tartalmaz egyetlen további pontot sem a két útról. Legyen ez az út PiR1…RlQj (lehet, hogy csak egy élből áll, ekkor nincsenek R-pontok). Vegyük a P1…Pi és Pi…Pk utak közül a hosszabbat (ha egyforma hosszúak, mindegy melyiket vesszük), és a Q1…Qj és Qj…Qk utak közül is a hosszabbat (ha egyforma hosszúak, itt is bármelyiket vehetjük). Illesszük ezeket össze a két utat összekötő PiR1…RlQj úttal: így egy utat kapunk amely U1 egyik végpontját köti össze U2 egyik végpontjával és nyilván hosszabb e két útnál (az összekötő út legalább egy élt tartalmaz, a két „félút” mindegyike legalább (k–1)/2 élt tartalmaz). Ez az ellentmondás bizonyítja a feladat állítását.
27. Erre az állításra két lényegesen különböző megoldást mutatunk.
1. MEGOLDÁS: Felhasználunk egy ismert feladatot: Ha egy könyvtárban egy napon t látogató járt, mindegyik csak egyszer, és bármely két látogató találkozott a könyvtárban, akkor volt olyan időpont, amikor minden látogató egyszerre volt a könyvtárban. (Ennek bizonyítása is a „vegyük a legszélsőt” elv egyszerű alkalmazása: Vegyük azt az időpontot, amikor először távozik valaki a könyvtárból, ekkor már mindenki ott van, mert aki nincs ott, azzal már nem találkozhatna.)
Ezután a bizonyítás a következő: Vegyünk egy leghosszabb utat a fában, ez lesz a „könyvtár”. Az előző feladat szerint ezt a fa minden további útja metszi. A 25. feladat szerint a közös rész egy út (vagy egy pont, amit most szintén útnak tekintünk). Ez pontosan azt jelenti, hogy a többi leghosszabb út tekinthető egy-egy látogatónak, és bármely látogató pontosan egyszer járt a „könyvtárban”. Hogy bármely két „látogató” „találkozott” is a „könyvtárban”, az most azt jelenti, hogy bármely három leghosszabb útnak van közös pontja. Ez viszont igaz, mert ha nem lenne, akkor – mivel bármely kettőnek találkoznia kell, volna kör. Az idézett feladatból mostmár következik, hogy az minden „látogató” „találkozott” a „könyvtárban”, vagyis az összes leghosszabb útnak van közös pontja.
2. MEGOLDÁS: Ismét használjuk az előző feladatot. Vegyünk egy leghosszabb utat, és vegyük ennek (egyik) középső pontját. Ha egy leghosszabb út nem menne ezen keresztül, akkor a metszésponttól indulva mindkét út hosszabbik felén, egy a leghosszabbnál hosszabb utat kapnánk.
28. Ha xy él, akkor d(x,y)=1. Az n pontú fának pontosan n–1 éle van, tehát ennyi párra lesz 1 d(x,y) értéke. A többi pontpárra d(x,y)≥2. Itt pontosan akkor áll minden más pontpárra egyenlőség, ha a fa csillag. Tehát a minumumot a csillag szolgáltatja: (n–1)2.
29. a) Ha bármely két össze nem kötött pontnak van közös szomszédja, akkor bármely két pont között van 1 vagy 2 élből álló út, tehát bármely két pont távolsága legfeljebb 2. Ha viszont bármely két pont távolsága legfeljebb kettő, akkor bármely két össze nem kötött x és y pont között van egy xuy út, s ekkor u közös szomszéd.
b) Ha egy szélességi faváz magassága kettő, akkor a gyökérből bármely pont elérhető legfeljebb kettő hosszú úttal, tehát bármely pontnak a gyökértől vett távolsága legfeljebb kettő. Ha ez bármely pontra igaz, akkor bármely két pont távolsága legfeljebb kettő, tehát a gráf átmérője 1 vagy kettő. De egy csak úgy lehet, ha a gráf teljes gráf, s ekkor bármely pontból induló szélességi faváza 1 magasságú.
30. Ha a gráf nem összefüggő, akkor legalább két összefüggő komponensre bomlik. Tíz pont esetén ez csak úgy lehet, ha van egy legfeljebb ötpontú összefüggő komponens. De az ilyen komponensben egy pont foka sem lehet nagyobb négynél. Ezzel beláttuk, hogy ha egy tízpontú gráfban minden pont foka legalább öt, akkor összefüggő. Ha itt öt helyett négyet írnánk, akkor már nem volna igaz az állítás: ellenpélda az a gráf, amelynek két komponense egy-egy teljes ötös. (Érdemes meggondolni, hogy van-e más ellenpélda?)
Az is igaz, hogy a gráf átmérője 2: legyen a gráf két pontja x és y. Azt kell belátnunk, hogy ha nincsenek összekötve, akkor van közös szomszédjuk. De ha nincsenek összekötve, akkor rajtuk kívül 8 pont van, s ezek közül öttel-öttel vannak összekötve. Ez pedig csak úgy lehet, ha van olyan pont, amellyel mindkettő össze van kötve.
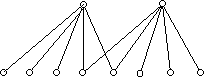
A két teljes ötös mutatja, hogy ha minden pont foka négy, akkor a gráf nem feltétlenül 2-átmérőjű, hiszen nem is feltételenül összefüggő.
Az általános esetben ha egy 2n pontú gráf nem összefüggő, akkor legalább két összefüggő komponensre esik szét, s ekkor a legkisebb komponensben legfeljebb n pont van, így ott minden pont foka legfeljebb n–1. A következő állítást kaptuk:
Ha egy 2n pontú gráfban minden pont foka legalább n, akkor a gráf összefüggő. Ha csak annyit követelünk meg, hogy minden pont foka legalább n–1 legyen, akkor a két pontdiszjunkt teljes n-esből álló 2n pontú gráf ellenpélda az állításra. (Érdemes meggondolni, hogy van-e más ellenpélda?)
Az általános esetben is igaz, hogy ha egy 2n pontú gráfban minden pont foka legalább n, akkor a gráf 2-átmérőjű. Ha ugyanis két pont nincs összekötve, akkor mindkettő legalább n-nel van összekötve a maradó 2n–2 pontból, s ez csak úgy lehetséges, ha van közös szomszédjuk. A két teljes n-es példája mutatja, hogy ez az állítás sem javítható.
MEGJEGYZÉS: Ha egy 2n pontú gráfban minden pont foka legalább n, akkor viszont sokkal több is igaz: nemcsak hogy összefüggő a gráf, hanem még az is igaz, hogy bármely pontját elhagyva is összefüggő marad. Tegyük fel ugyanis, hogy van olyan x pontja, amelyet elhagyva a gráf szétesik több komponensre. Legyenek ezek a komponensek K1, K2, …, Km. Legyen K1 a legkisebb pontszámú közöttük. Mivel m≥2, ezért K1 pontszáma legfeljebb n–1. Legyen y K1 egy pontja. Ez a pont csak K1 pontjaival és esetleg x-szel lehet összekötve. Ezért fokszáma legfeljebb n–1, ami ellentmondás. Azt is beláttuk tehát, hogy ha egy 2n gráfban pontú gráfban minden pont foka legalább n, akkor nincs benne elvágó pont, vagyis kétszeresen összefüggő. Ha viszont az n–1-es fokszám is meg van engedve, akkor már az sem biztos, hogy összefüggő.
Valójában még ennél is több igaz minden ilyen gráfra. Az is igaz, hogy van benne Hamilton-kör is (ami egy sokkal erősebb foka az összefüggőségnek). Erről majd a következő, a Hamilton-körökről (is) szóló fejezetben lesz szó (lásd Dirac tételét**).
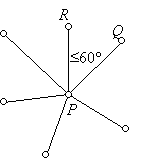
31. a) Ha egy P pontból menne hat él különböző pontokhoz, akkor volna ezek között kettő, Q és R, amelyekre QPRÐ ≤ 60° volna. Így QR nem lehet a háromszög legnagyobb oldala. A szimmetria miatt feltehetjük, hogy PQ a háromszög legnagyobb oldala, s ekkor PQ nem lehetne behúzva a távolsággráfban (mind P-hez van Q-nál közelebbi pont: R, mind Q-hoz van P-nél közelebbi pont: R).
Ugyanez az állítás a leghosszabb szakaszokból álló távolsággráfban nem igaz, hiszen az még csillag is lehet: ha n–1 pontot „egy kupacban” veszünk fel, például egy egységkör belsejében, és az n-edik pontot ettől „jó távol”, például legalább 3 egységnyi távolságra a kör középpontjától.
b) Belátjuk, hogy a távolsággráf körmentes: Ha P1 P2… Pn P1 egy kör volna a gráfban, akkor ez a gráfelméleti kör egy geometriai sokszöget határozna meg. Feltehetjük, hogy P1P2 e sokszög leghosszabb oldala. P3 közelebb van P2-höz, mint P1, Pn közelebb van P1-hez, mint P2, tehát P1P2 sem P2, sem P1 miatt nem lehet behúzva. Ez ellentmondás, tehát nem lehet kör a gráfban.
Ez a bizonyítás ugyanígy megy legrövidebb helyett leghosszabb szakaszokra is, tehát b)-t mindkét fajta távolsággráfra beláttuk.
b)-ből viszont következik d), hiszen n pontú körmentes gráfnak legfeljebb n–1 éle van, és ha egy gráfban minden pontból indul ki él, akkor legalább n/2 éle van. Másrészt a 24. feladat alapján következik az is, hogy van egy legalább n/2 pontú üres részgráfja, tehát c) is igaz.
32. Ha a gráf nem összefüggő, akkor több összefüggő komponensre bomlik. Legyen az egyik komponens ponthalmaza A, ez lesz az egyik osztály, az összes többi pontot a másik osztályba tehetjük: A és a többi pont között nem fut él a gráfban. Másrészt ha a gráf pontjait sikerült A és B osztályba sorolnunk úgy, hogy egyik sem üres és a két osztály között nem fut él, akkor a gráf nyilván nem összefüggő.
33. Ha a gráf összefüggő, kész vagyunk. Ha nem az, akkor a pontjai két nem üres osztályba sorolhatók úgy, hogy a két osztály pontjai között nem fut él. Legyen a két osztály A és B. Ekkor minden A-t B-vel összekötő él a gráf komplementerében van. Ezért A bármely pontjából el lehet jutni B bármely pontjába éllel és onnan vissza A bármely másik pontjába. Ezzel azt az erősebb állítást is beláttuk, hogy ha egy gráf nem összefüggő, akkor komplementere 2-átmérőjű. Vagyis vagy összefüggő a gráf is, a komplementere is, vagy az egyik nem összefüggő, a másik 2-átmérőjű.
34. Addig veszünk hozzá a részgráfhoz éleket a gráfból, amíg hozzá tudunk venni anélkül, hogy kört kapnánk. Az így kapott részgráf körmentes lesz (úgy csináltuk) és összefüggő: ha komponensekre esne szét, azok között menne él a gráfban, s ezt az élt hozzávehetnénk anélkül, hogy kört zárnánk be, hiszen végpontjai között még nem megy út a részgráfban. A kapott részgráf tehát (kapta)fa, faváz.
35. Az veszít, akinek az n-edik élt kell behúznia, mert ha még csak legfeljebb n–2 él van behúzva, akkor a gráf (F) szerint biztosan nem összefüggő. Két különböző komponensbe tartozó élét összekötve biztosan nem zárunk be kört, így az n–1-edik él behúzásáig nem kell kört bezárnunk. Aki viszont az n-edik élt kényszerül behúzni, az biztosan hoz létre kört, mert n élű gráf a 2. feladat szerint nem lehet körmentes.
36. n–1 mérkőzés mindig elég. Párosítsuk például a versenyzőket, ha páratlan sokan vannak, akkor egyikük legyen erőnyerő és párosítsuk a többit. Ezek közötti mérkőzés nyertesei és az erőnyerő jut a következő fordulóba, ahol ismét párosítjuk az „állva maradt” versenyzőket. Ha páratlan sokan maradtak állva, egyikük erőnyerő lesz. Ezt addig csináljuk, amíg csak egy versenyző maradt állva. Mivel minden mérkőzésen egy valaki esett ki, éspedig olyan, aki eddig versenyben volt (tehát korábban csak nyert), ezért pontosan n–1 mérkőzés lejátszása után marad egy versenyző: ő a legerősebb.
Másrészt kevesebb mérkőzés sehogyan sem lehet elég, mert ha legfeljebb n–2 mérkőzést játszottak le, akkor a mérkőzések gráfja még nem összefüggő, tehát több komponensre bomlik a gráf. Minden komponensben van egy legerősebb és ezek közül bármelyik lehet a legerősebb, ezt még nem tudjuk eldönteni.
MEGJEGYEZZÜK, hogy a megadott lebonyolítás a kupamérkőzések eredeti lebonyolítási elve. A „kihívásos” versenyeken más módszert alkalmaznak: egy versenyző „kihív” egy másikat, majd a győztesnek kell kihívnia a következőt, és így tovább, amíg már mindenki mérkőzött egyet. Az „állva maradó” versenyző a legjobb. Itt is minden mérkőzésen egy valaki esik ki, tehát n–1 mérkőzés után lesz győztes.
37. A második legerősebb csak olyan valaki lehet, aki a legerősebbtől kapott ki az előző feladat („kupamérkőzéses”) versenyén. Nyilván akkor tudjuk a leggyorsabban kiválasztani, ha bárki is nyer, az kevés mérkőzést játszott, vagyis a lehető legegyenletesebben kell a versenyt lebonyolítani. Ezt 2m versenyző esetén úgy érhetjük el, ha az előző feladatban alkalmazott lebonyolítási módot alkalmazzuk. Ekkor egyetlen fordulóban sincs erőnyerő és így bárki is a győztes, pontosan m mérkőzést játszott, tehát a második helyre még m jelölt van: azok, akiket ő vert meg. Ezek közül kell a legjobbat megkeresnünk, amit m–1 mérkőzéssel megtehetünk. Azt kaptuk, hogy 2m+m–2 mérkőzéssel megtalálható a két legerősebb versenyző. Ha nem pont kettőhatvány számú versenyző van, akkor is célszerű úgy csinálni, hogy az első fordulóba berakunk annyi „fiktív” versenyzőt, hogy a versenyzők száma kiegészüljön kettőhatványra, és a fiktív versenyzők partnerei az első fordulóban erőnyerők. A többi fordulóban már nem lesz erőnyerő.
Ha n versenyző van és 2m–1<n<≤2m, akkor m+n–2 (vagy ennél eggyel kevesebb) mérkőzés kell a második legjobb kiválasztásához.
Belátható, hogy kevesebb nem elég.
38. Megmutatjuk, hogy [(3n–2)/2] mérkőzés elég. Csináljuk a következőt: ha n=2m páros, akkor az első fordulóban párosítsuk az összes résztvevőt, ez m mérkőzést jelent. Ezután az m nyertesből m–1 mérkőzéssel kiválasztható a legerősebb, az m vesztesből viszont ugyanazzal a módszerrel (csak itt mindig a vesztes jut tovább!) m–1 mérkőzéssel kiválasztható a leggyengébb. Ez összesen 3m–2=3n/2–2 mérkőzés.
Ha n=2m+1 páratlan, akkor az első fordulóban lesz egy erőnyerő. Közbeiktatunk a kedvéért egy „külön fordulót”, amelyben ő játszik az egyik győztessel. Ez eddig m+1 mérkőzés, amely után m győztes marad és m+1 vesztes. Az előbbiekből m–1 mérkőzéssel kiválasztjuk a legerősebbet, az utóbbiak közül m mérkőzéssel a leggyengébbet. Ez összesen 3m=3(n–1)/2 mérkőzés. Mindkét eredmény felírható [3(n–1)/2] alakban.
MEGJEGYZÉS: Kevesebb nem mindig elég. Ennek bizonyítása megtalálható például
39. a) Elég megmutatni, hogy egy olyan fában, amelyben van él (tehát nem egy pontból áll), van legalább két elsőfokú pont. Egy ilyen fában nem lehet izolált pont, tehát minden pont foka legalább egy. Ha csak egy elsőfokú volna, akkor az összes többi pont foka legalább kettő volna, így a fokszámok összege legalább 2(n–1)+1 volna, de a fokszámok összege az élszám kétszerese, azaz 2n–2.
Másik megoldás: Ha a gráfnak van éle, akkor a leghosszabb útjában is van él, tehát két végpontja különböző. De a leghosszabb út két végpontja biztosan elsőfokú, különben a gráfban volna kör, hiszen a leghosszabb út végpontjából bármely további él csak az út egy pontjához vezethetne.
MEGJEGYZÉS: Hasonló gondolatot használtunk a fejezet
1. feladatában is.
b) Ha a fának
n pontja van, akkor
n–1 éle van, tehát a fokszámok összege 2(
n–2). Ha két elsőfokú pont van, akkor az összes többi pont fokszáma legalább kettő, így a fokszámok összege legalább 2+2(
n–2)=2
n–2. Másrészt pontosan ennyi a fokszámok összege, tehát az összes többi pont foka kettő. Vagyis a fa egy út.
40. Ha egy gráfban nincs páratlan kör, akkor a gráf a 18. feladat után adott jellemzés szerint páros gráf, vagyis pontjai két osztályba sorolhatók úgy, hogy a gráf minden éle a két osztály között fut. Ha az egyik osztályban k pont van, akkor a másik osztályban n–k pont van, így a gráfban maximálisan k(n–k) él van: ha a két osztály között minden él be van húzva. A számtani és mértani közép közötti egyenlőtlenség szerint k(n–k)<≤n2/4. Ha n páros, akkor ez a pontos érték: k=n/2 esetén (tehát ha mindkét osztályban n/2 pont van) az élek száma pontosan n2/4. Ha viszont n páratlan, akkor n2/4 nem egész, tehát a nála kisebb legnagyobb egész, (n2–1)/4 a maximális élszám. Ez akkor lép fel, ha az egyik osztályban (n–1)/2 él van, a másikban (n+1)/2.
MEGJEGYZÉS:
Az olyan páros gráfot, amelynek két pontosztálya
között minden él be van húzva,
teljes páros gráfnak nevezzük. Ha a két osztályban
k, illetve
l pont van, akkor
k+
l pontú teljes gráfról beszélhetünk.
41. Ha a háromszögek súlypontjait vesszük egy gráf pontjainak és két ilyen pontot összekötünk, ha a megfelelő háromszögek határosak, akkor az így kapott gráf fa.
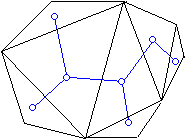
Ugyanis a behúzott átlók és a gráf élei között egy-egyértelmű megfeleltetés van, másrészt a gráf nyilván összefüggő, n–2 pontja van (mert ennyi háromszög van) és eggyel kevesebb éle, mert n–3 átlót húztunk be. Tehát ez a gráf fa, amelynek n>3 miatt van éle, így a 39a. feladat szerint legalább két elsőfokú pontja van. Az elsőfokú pontnak pedig olyan háromszög felel meg, amelyet csak egy átló határol, ez pedig pontosan akkor fordul elő, ha a háromszög határa két oldal és egy legrövidebb átló. Ha n > 4, akkor a két elsőfokú pont nem szomszédos, így a két legrövidebb átló nem lehet azonos. (Ha n=4, akkor a két háromszögnek ugyanaz az átló a határa.)
42. Fa esetén az egyenlőség következik abból, hogy az n pontú fa élszáma n–1, és abból, hogy a fokszámösszeg kétszerese az élszámnak. A fordított állítást teljes indukcióval bizonyítjuk. Az állítás n=1,2-re semmit mondó, feltehető, hogy n>2.
Tegyük fel, hogy n–1 számra tudjuk az állítást. Ha adott n pozitív egész szám, amelyek összege 2n–2, akkor a legkisebb nyilván egy, különben az összeg legalább 2n volna. Legyen ez di. Másrészt a legnagyobb nyilván nagyobb egynél, különben az n szám mindegyike egy volna, így az összegük n<2n–2 volna. Legyen a legnagyobb dj. Hagyjuk el az n szám közül di-t és csökkentsük eggyel dj-t. Ekkor n–1 számot kapunk, amelyek mindegyike továbbra is pozitív és összegük 2n–4 = 2(n–1)–2, tehát alkalmazható az indukciós feltevés: van olyan fa, amelynek fokszámai rendre ezek a számok. Legyen xj az a pont, amelynek fokszáma dj–1. Illesszünk a gráfhoz egy xjy élt, amely tehát ezt a pontot egy új ponttal köti össze. A gráf nyilván továbbra is fa marad, hiszen összefüggő marad és nem keletkezik benne kör. Másrészt minden pont fokszáma változatlan marad, csak xj fokszáma lesz eggyel nagyobb, azaz éppen dj, keletkezik továbbá egy elsőfokú pont, vagyis di-fokú pont. Ezzel az indukciós lépést befejeztük.
43. A számok között van (legalább) egy legnagyobb. Ha ez az A csúcson áll, akkor az A-val szomszédos csúcsokon nem szerepelhet kisebb szám (különben valamelyik szomszédon nagyobb szerepelne). Tehát A minden szomszédján is a legnagyobb szám áll, így a vele szemközti háromszög lapon levő D szomszédján is. D-re ugyanezt elmondhatjuk, és így azt kapjuk, hogy mind a hat csúcson ugyanaz a szám áll.

44. Kockára ugyanígy megy a bizonyítás, hiszen csak annyit használunk, hogy a) van legnagyobb a csúcsokra írt számok között, b) ha egy csúcson a legnagyobb szám áll, akkor minden szomszédján is a legnagyobb szám áll, c) bármely csúcsból el lehet jutni minden más csúcshoz élek mentén, vagyis a test gráfja összefüggő.
Tehát a következőt kaptuk: ha egy véges összefüggő gráf minden csúcsára egy-egy valós számot írunk úgy, hogy minden csúcson a szomszédos csúcsokon álló számok számtani közepe áll, akkor minden csúcsra ugyanazt a számot kellett írnunk.
Ha a gráf nem véges, de összefüggő, akkor az állítás már nem feltételenül igaz, mint ezt a számegyenes egészei mutatják (minden számot a két szomszédjával kötünk össze): itt bármely kettő a két szomszédjának számtani közepe. Végtelen gráfnál összefüggőségen kívül azt is fel kell tennünk, hogy van a felírt számok között legnagyobb, vagy legkisebb.
45. A gráf pontjai legyenek a számok, két pont akkor van össze-kötve, ha a hozzájuk tartozó két szám összege racionális. Ha a gráfban van páratlan hosszú kör, akkor e kör minden pontjához tartozó szám raconális. Ugyanis pl.
2a1 = (a1 + a2) – (a2 + a3) + (a3 + a4) – (a4 + a5) + … – … + (a2k–1 + a1)
racionális, s így a1 is. Ha a gráfban nem volna páratlan kör, akkor a 18. feladat után adott jellemzés szerint páros gráf volna, s ha ennek két osztályában k és n–k pont van, akkor az élek száma maximum k(n–k), ami legfeljebb [n2/4]. (Lásd a 40. feladatot és megoldását) Ez n≥5 esetén kevesebb a feladat feltételében szereplő élszámnál. Tehát a gráfban van páratlan kör, s így vannak olyan pontok, amelyek racionális számhoz tartoznak. Nyilvánvaló, hogy minden olyan ponthoz is racionális szám tartozik, amely egy ilyen ponttal van összekötve. Ebből következik, hogy ha egy ponthoz racionális szám tartozik, akkor az összes, vele azonos komponensben levő ponthoz is racionális szám tartozik. A megadott élszám mellett azonban a 21. feladat szerint összefüggő, így azt kapjuk, hogy minden szám racionális. S ekkor az összes összeg is racionális.
46. Az első esetben a Másodiknak van nyerő stratégiája. A következőt csinálja: ha van olyan csupa színes élből álló út, amelyet egy él behúzásával körré lehet zárni, akkor ezt az élt húzza be. Ha nincs, akkor az Első által legutoljára behúzott élnek a főátlóra való tükörképét húzza be. Így minden lépés után a főátlóra szimmetrikus gráfot hagy maga után, feltéve, hogy nem nyert. Ebből következik, hogy mindig fog tudni lépni, hiszen az Első mindig megbontja a szimmetriát. Még az volna elképzelhető, hogy az Elsőnek sikerül (színes) kört bezárnia. Tekintsük azt az utat, amelyet az Első körré zár be. Ha ez az út nem metszené legalább kétszer a főátlót, akkor a főátlóra vett tükörképe is színes út volna, hiszen a Második lépése után mindig szimmetrikus a gráf a főátlóra. Ez az út is egy éllel körré zárható volna, és a két út közül legalább az egyik nem tartalmazza a Második által utoljára behúzott élt. Tehát legalább az egyik út olyan, hogy azt a Második körré zárhatta volna, s ez esetben a stragégia szerint meg is tette. Ez az eset tehát nem jöhet létre. Ez a meggondolás mindig érvényes, ha az Első által talált színes útnak és tükörképének nincs közös éle. Ha van, akkor a közös él tükörképe is közös él, és a főátló másik oldalán helyezkedik el (a főátlóra nem illeszkedik él). De ekkor az Első által talált út legalább kétszer metszi a főátlót, vagyis a főátló az utat legalább két éldiszjunkt útra bontja. Vegyük ezek közül az (egyik olyan) P utat, amelynek két végpontja a főátlón van. Ennek a főátlóra vett P’ tükörképe is csupa színes élből áll, hiszen a Második szimmetrikus gráfot hagyott maga után. De P’ és P ugyanabban a két pontban éri el a főátlót, tehát P és P’ együtt a gráf egy ciklusát alkotja, s így tartalmaz egy kört. A színes élek tehát legalább egy kört már tartalmaznak, így Elsőnek már nincs módja lépni. Első tehát nem nyerhet, így (mivel a játék véges) a Második nyer.
A fordított játékban elég azt meggondolni, hogy pontosan akkor feszítenek kört a színes élek, ha a nem-színes élek által alkotott gráf (az összes ponton, tehát az (n+1)2 ponton) nem összefüggő. Vagyis akkor kényszerül valamelyik játékos színes kört bezárni, ha a nem-színes élekből alkotott gráf fa, azaz n2+2n éle van. Eredetileg 2n(n+1)=2n2+2n nem színes él van, tehát (ha mindketten jól játszanak) az veszít, akinek az n2+1-edik élt kell behúznia. Vagyis páros n-re az Első nyer, páratlanra a Második.
47. A feladat gráfelméleti nyelven így hangzik: egy gráfban minden pont foka legfeljebb öt és bármely két pont távolsága legfeljebb négy(!). Hány pontja lehet maximálisan a gráfnak?
Gondoljuk meg először, hogy miért biztos egyáltalán, hogy nem lehet akármilyen sok pontja. A megoldásra nyilvánvalóan kínálkozik a szélességi faváz. Keressük meg egy tetszőleges x ponthoz tartozó szélességi favázát a gráfnak. Miután minden pont foka legfeljebb öt, ezért az első szinten legfeljebb öt pont lesz és minden további szinten az előző szint pontszámának legfeljebb négyszerese. Másrészt bármely két pont távolsága legfeljebb négy, ezért maximálisan négy szint lesz az x gyökéren kívül. Tehát valóban csak korlátos sok pontja lehet a gráfnak. Egyelőre az 1+5+20+100+400=526 felső korlátot kaptuk, ez azonban még túl sok pont: ha lerajzoljuk a fát, kiderül, hogy ebben a legfelső szint pontjai között olyanok is vannak, amelyek egymástól négy helyett nyolc távolságra vannak. Tehát ennél csak jóval kevesebb pont lehet. Megpróbálhatjuk ezt az eljárást folytatni, de akkor meg kell gondolnunk, hogy mit csinálunk az esetleg fellépő körökkel. Célszerűbb megpróbálni ügyesen megválasztani az x pontot: úgy, hogy biztosan alacsonyabb legyen a szélességi faváz. S valóban: vegyük a gráf (egyik) leghosszabb útját. Ez a feladat feltétele szerint legfeljebb négy hosszúságú. Feltehetjük, hogy potosan négy hosszúságú (MIÉRT?!). Legyen x ennek középső pontja. Azt állítjuk, hogy az x gyökerű szélességi faváz már csak kétszintes lehet. Tegyük fel ugyanis, hogy van egy y pont a faváz harmadik szintjén. Az y pontból a gyökérhez vezető út az első szintről pontosan egy pontot tartalmaz, legyen ez z. Az a leghosszabb út, amelynek x a középső pontja, két kettő hosszú, x-ből induló útra bomlik, s ezek közül (legalább) az egyik nem tartalmazza z-t, s így az yz út egyetlen pontját sem. Ha ezt az utat hozzáillesztjük az y-ből x-be menő úthoz, akkor egy öt hosszú utat kapunk, ami ellentmond a feladat feltételének.
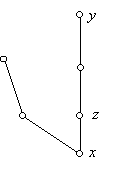
Tehát az x gyökerű szélességi faváz valóban legfeljebb kétemeletes. Ezért legfeljebb 1+5+20=26 pontja van.
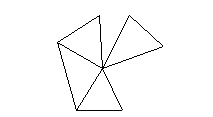
Ha felrajzoljuk azt a fát, amelynek első szintén öt pont van és minden pontjából négy második szintű ponthoz indul él, akkor ez a gráf megfelel a feladat feltételeinek. Tehát 26 a pontos válasz.
48. a) Nyilván elég az állítást a gráf feszítő fájára igazolni (MIÉRT?). Vegyük a gráf (egyik) leghosszabb, 2k hosszú útját és egészítsük ki ezt favázzá. Ezt a 34. feladat szerint megtehetjük. Nyilván a faváznak is ez a(z egyik) leghosszabb útja. Vegyük a középső pontját, legyen ez x, két útbeli szomszédja y és z. Ha x-ből indulna ki k-nál hosszabb U út a favázban (vagyis a faváz magassága nagyobb volna k-nál), akkor ez az út y és z közül csak az egyiket tartalmazhatja, például y-t, és minden további pontja y utódja volna. De akkor ezt az U utat hozzáillesztve a leghosszabb út z-t tartalmazó „félútjához” kapnánk egy 2k-nál hosszabb utat, ami ellentmondás. Ezzel bebizonyítottuk az állítást.
Kérdés: hol használtuk ki, hogy favázat vettünk az elején?
b) Ez nyilvánvalóan nem igaz, már akkor sem, ha a gráf egy út: például a végpontjai között ugyanakkora a távolság, mint a leghosszabb út hossza.
49. a) Ha egy gráf 2-átmérőjű, akkor összefüggő, tehát n pont esetén legalább n–1 éle van. Másrészt a csillag olyan 2-átmérőjű n pontú gráf, amelynek pontosan n–1 éle van. Tehát a minimális élszám n–1. Könnyen belátható az is, hogy más 2-átmérőjű fa nincs, ez következik b)-ből:
b) Ha x elsőfokú és y a(z egyetlen) szomszédja, akkor y minden más ponttal is össze van kötve, mert ha egy z ponttal nem lenne összekötve, akkor x-nek és z-nek nem volna közös szomszédja, tehát x és z távolsága nem lehetne 2, azaz a gráf nem volna 2-átmérőjű. Az állítás tehát igaz: Ha egy 2-átmérőjű gráfban van elsőfokú pont, akkor annak szomszédja telített pont.
Ennek alapján már könnyen belátható, hogy az n pontú, n–1 élű gráfok közül csak a csillag 2-átmérőjű: egy n pontú, n–1 élű összefüggő gráf fa, tehát van elsőfokú pontja, s annak szomszédja telített pont. Tehát valóban csillagról van szó.
c) Hárompontú 2-átmérőjű gráf csak kettő van: a két élből álló út és a teljes hármas. Mindkettőben van telített pont, tehát hárompontú 2-átmérőjű gráfban van telített pont.
Ha egy négypontú 2-átmérőjű gráfban nincs telített pont, akkor minden pont foka legfeljebb kettő. Másrészt elsőfokú pont sem lehet benne b) szerint. (Izolált pont pedig nem lehet benne az összefüggőség miatt.) Tehát minden pont foka kettő. Ilyen négypontú gráf csak egy van: a négy hosszú kör.
Ha egy ötpontú 2-átmérőjű gráfban nincs telített pont, akkor minden pont foka legfeljebb három. Másrészt nincs benne izolált pont és nincs benne elsőfokú pont sem b) szerint. Tehát minden pont foka 2 vagy 3. Nem lehet minden pont foka 3, hiszen páros sok páratlan fokú pontja van (lásd az I. fejezet 20. feladatát). Tehát van egy másodfokú pontja. Azt is tudjuk, hogy vagy egy vagy három másodfokú pontja van, vagy minden pontja másodfokú. Az utóbbi esetben egy öt hosszú körről van szó, amely valóban 2-átmérőjű (!). Ha csak egy másodfokú pont van, legyen ez x és legyen két szomszédja y és z és legyen u és v a két további pont. Ezek csak úgy lehetnek harmadfokúak, ha össze vannak kötve y-nal is, z-vel is és egymással is, hiszen x-szel nincsenek összekötve. A következő gráfot kaptuk:
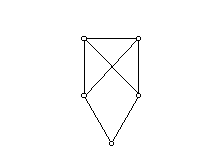
Ezt a gráfot leírhatjuk úgy, hogy ötszög két „metsző” átlóval. Végül ha három másodfokú és két harmadfokú pont van, akkor két eset lehetséges: ha a két harmadfokú pont van összekötve, akkor az összekötő élt elhagyva egy 2-reguláris gráfot kapunk, s ez öt pont esetén csak az ötszög lehet, tehát az így kapott gráf az ötszög egy átlóval. Ha viszont a két harmadfokú pont nincs egymással összekötve, akkor a következő gráfot kapjuk:
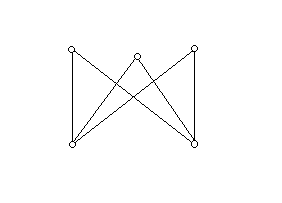
Ez a 2+3 pontú teljes páros gráf.
Végeredményben a következő ötpontú, 2-átmérőjű, telített pont nélküli gráfokat találtuk: az ötszög, az ötszög egy átlóval, az ötszög két egymást metsző átlóval és a 2+3 pontú teljes páros gráf.
d) A páros gráf csak úgy lehet 2-átmérőjű, ha bármely két, különböző osztályba tartozó pont össze van kötve. Ha ugyanis az x és y pont különböző osztályba tartozik, akkor nem lehet kettő hosszú úttal összekötve (és semmilyen páros élhosszú úttal sem lehet összekötve). Vagyis csak a teljes páros gráfoknak 2 az átmérője. Azok viszont nyilvánvalóan 2-átmérőjűek.
e) Ha egy körnek legalább hat pontja van, akkor van két olyan pontja, amely a kör mentén mindkét irányban legalább három távolságra van. Ha a gráfnak nincs további éle, akkor nem lehet 2-átmérőjű. Tehát csak a három-, négy- és ötpontú kör 2-átmérőjű.
f) A b) rész szerint a gráfban nem lehet elsőfokú pont. Legyen x egy minimális fokú pont a gráfban és legyen a fokszáma k, k≥2. Ha minden pont foka legalább három, akkor a gráfnak legalább 3n/2 éle van, nincs mit bizonyítanunk. Feltehetjük tehát, hogy k=2. A 29. feladat szerint az x gyökerű szélességi faváznak két emelete van. Az első emeleten van x két szomszédja, a második emeleten vannak x másodszomszédai, ez további n–3 pont. A szélességi faváznak n–1 éle van, a második szinten levő n–3 pont legalább másodfokú, viszont a favázban elsőfokú, tehát a gráfban mindegyik ilyen pontból indul ki legalább még egy él. Ez összesen legalább (n–3)/2 további él.
A gráfnak tehát legalább n–1+(n–3)/2=(3n–5)/2 éle van, s ezt akartuk bizonyítani.
g) A c) részben talált 2+3 pontú teljes páros gráf mintájára könnyen találunk olyan 2-átmérőjű, telített pont nélküli gráfot, amelynek n pontja és 2n–4 éle van: ilyen a 2+(n–2) pontú teljes páros gráf, azaz az a páros gráf, amelynek egyik osztályában két pont van, a másikban n–2 pont és a különböző osztályba tartozó pontok között minden él be van húzva. De kérdés, hogy nincs-e ennél kevesebb élű is? A c) részben láttuk, hogy n=4-re nincs, de n=5-re van: az ötszög. A 2+n–2 pontú teljes gráf megkapható úgy is, hogy veszünk egy kettő hosszú xuy utat – ez 2 átmérőjű gráf! –, és középső pontját, u-t „megsokszorozzuk”, azaz felveszünk még n–3 pontot és azt is összekötjük az út két végpontjával, x-szel és y-nal. Általában is igaz, hogy ha egy 2-átmérőjű gráfban van egy u másodfokú pont, akkor azt ily módon megsokszorozhatjuk, vagyis: ha felveszünk további pontokat, amelyeket összekötünk u két szomszédjával, akkor ismét 2-átmérőjű gráfot kapunk. Hiszen ha u-ból bármely pontba el lehetett jutni legfeljebb kettő hosszú úttal, akkor az újonnan felvett pontokból is el lehet jutni bármely régi pontba. Másrészt bármely két új pont között is van kettő hosszú út.
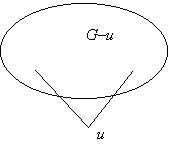
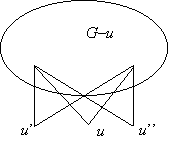
(Természetesen az állítás akkor is igaz marad, ha u fokszámáról nem mondunk semmit, és az új pontokat u összes szomszédjával összekötjük.) Ezzel viszont beláttuk, hogy akármilyen n≥5-re van olyan n pontú, telített pont nélküli 2-átmérőjű gráf, amelynek 2n–5 éle van, s ezt az ötszögből kaphatjuk úgy, hogy valamelyik pontját megsokszorozzuk (vagy akár két másodszomszéd pontját is megsokszorozhatjuk):
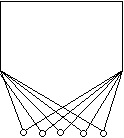

h) Ezek után a pontszámra vonatkozó teljes indukcióval belátjuk, hogy ha n≥5, akkor egy n pontú, 2-átmérőjű, telített pont nélküli gráfnak legalább 2n–5 éle van. n=5-re már c)-ben beláttuk ezt.
A f) részhez hasonlóan most is induljunk ki egy minimális fokú pontból, legyen ez x és legyen x fokszáma k. Most is tudjuk, hogy k≥2. Másrészt ha minden pont fokszáma legalább négy, akkor a gráfnak legalább 2n éle van, tehát nincs mit bizonyítanunk. Ezek szerint k=2 vagy 3. Tekintsünk egy x gyökerű szélességi favázat. Legyen először k=3.
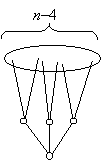
Az első emeleten ekkor három pont lesz, a második emeleten van a további n–4 pont. A favázban ezek mindegyike elsőfokú, a gráfban viszont legalább harmadfokú, tehát mindegyikből indul ki további legalább két-két él. Ez összesen még legalább további n–4 él, a faváznak n–1 éle van, vagyis a gráfnak legalább n–1+n–4=2n–5 éle van.
Marad az az eset, ha k=2. Ekkor az első emeleten van x két szomszédja, a második emeleten vanak x másodszomszédai, ez most n–3 pont.
Hagyjuk el a faváz éleit, ez n–1 élt jelent. Azt kell belátnunk, hogy legalább n–4 él marad. Elég tehát belátnunk, hogy a második szinten levő pontok fokszámösszege a faváz éleinek elhagyása után 2(n–4).
Tudjuk, hogy a gráf minden pontja eredetileg legalább másodfokú, tehát a második szinten a faváz éleinek elhagyása után minden pont legalább elsőfokú. Ha legfeljebb két elsőfokú van (tehát a gráfban legfeljebb két másodfokú pont van ezen a szinten), akkor a második emeleti pontok fokszám összege legalább 2+2(n–5)=2(n–4), amit bizonyítanunk kell.
Marad az az eset, ha a második szinten legalább három másodfokú pont van. Ebben az esetben kicsit pontosabban kell számolnunk. Használni fogjuk az indukciós feltevést is, éspedig olyan formában, hogy elhagyunk egy pontot a gráfból. Nyilván célszerű a legkisebb fokú pontot elhagyni, tehát egy másodfokú pontot. Ha az elhagyásával keletkező gráfban fennállnak az indukciós feltevés használásához szükséges feltevések, akkor e gráfban legalább 2(n–1)–5=2n–7 él van, s ha ehhez hozzávesszük az elhagyott két élt, akkor az eredeti gráfban legfeljebb 2n–5 él van, s ezt akarjuk bizonyítani.
Nézzük tehát először, hogy a másodfokú x pont elhagyása után keletkezhet-e telített pont a G\x gráfban.
Tegyük fel, hogy keletkezett egy t telített pont. Ez a t nem lehet az x pont valamelyik szomszédja (azaz nem lehet az x gyökerű szélességi faváz első emeletén), mert akkor t a G gráfban is telített pont volna, lévén, hogy x-szel is össze van kötve. Ha a második emeleten van, akkor a faváz éleinek elhagyása után is marad legalább n–3 (t-ből induló) él, hiszen t G-ben n–2-ed fokú és a favázban elsőfokú. Ez esetben a G gráfban legalább 2n–4 él van, s ez több, mint amit bizonyítani akarunk.
Azt kaptuk, hogy G\x-ben nincs telített pont. Ha tehát G\x 2-átmérőjű, akkor alkalmazhatjuk az indukciós feltevést, és kész vagyunk.
Minthogy x tetszőleges másodfokú pont volt G-ben, a továbbiakban feltehetjük, hogy ha z másodfokú, akkor a G\z gráf nem 2-átmérőjű. Ám ha z két szomszédjának volna egy további z’ közös szomszédja, vagy két szomszédja össze lenne kötve, akkor G\z 2-átmérőjű volna:
Legyen ugyanis u és v a G\z gráf két, éllel össze nem kötött pontja. A G gráf 2-átmérőjű, tehát van a gráfban kettő hosszú uyv út. Ha y≠z, akkor ez az út benne van a G\z gráfban is. Ha viszont y=z, akkor u és v az z pont két szomszédja. De ekkor az első esetben uz’v is út és benne van G\z-ben is, a második esetben uv 1 hosszú út G\z-ben. Azt kaptuk, hogy ha u és v G\z gráf két, éllel össze nem kötött pontja, akkor van közöttük egy vagy kettő hosszú út G\z-ben. Ez pontosan azt jelenti, hogy G\z valóban 2-átmérőjű – vagy esetleg 1-átmérőjű!
A továbbiakban tehát feltehetjük, hogy ha z másodfokú, akkor két szomszédja között nem fut él és két szomszédjának nincs több közös szomszédja.
Legyen tehát x egy másodfokú pont. Ha felrajzoljuk az x gyökerű szélességi fát, és u-val és v-vel jelöljük x két szomszédját, akkor az aláhúzott állítás szerint u-nak és v-nek x-en kívül nincs közös szomszédja, és uv nem éle a gráfnak. Jelöljük U-val, illetve V-vel az u, illetve v pont x-től különböző szomszédainak halmazát. Ezek egyike sem lehet üres, mert ha például U üres volna, akkor u elsőfokú volna, ami c) szerint maga után vonná, hogy G-ben van telített pont. Szintén az aláhúzott állításból következik, hogy u nincs összekötve V pontjaival, v nincs összekötve U pontjaival:
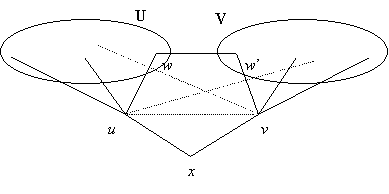
Ezután térjünk vissza oda, hogy a faváz második emeletén van legalább három másodfokú pont, legyen ezek egyike w∈U. Az aláhúzott állítás szerint w másik szomszédja nem lehet U-ban, de nem lehet v és x sem, vagyis w másik szomszédja V-ben van, jelöljük ezt w’-vel. Ahhoz, hogy w-ből el lehessen jutni kettő hosszú úttal V minden pontjába, w’-nek össze kell kötve lennie V minden pontjával, hiszen w másik szomszédja, u egyikkel sincs összekötve.
Megjegyezzük, hogy az így talált,
w’-ből induló |
V| él „új” él a favázhoz képest.
Tegyük fel, hogy V-ben is van egy másodfokú pont, z. Ennek v-től különböző szomszédja, z’ az előzőek szerint U-ban van és össze van kötve U minden pontjával. De ekkor a w’-ből induló |V| „új” él és a z’-ből induló |U| „új” él összesen |U|+|V|=n–3 „új” él, s ez a faváz további n–1 élével együtt ismét legalább 2n–4 él.
A továbbiakban tehát feltehető, hogy minden másodfokú pont U-ban van. Legyen z∈U egy további másodfokú pont. Ekkor z másik szomszédja, z’ V-ben van, és össze van kötve annak minden pontjával. Nem lehet z’=w’, mert akkor például z két szomszédja, u és z’ megegyezne w két szomszédjával, és ez ellentmond az aláhúzott állításnak. Így a második emelet minden másodfokú pontja U-ban van és mindegyikhez van egy-egy különböző pont V-ben, amellyel össze van kötve, s amely V minden pontjával össze van kötve. Viszont legalább három másodfokú pont van a második emeleten, ez legalább három különböző ilyen pontot jelent V-ben, vagyis V legalább három pontból áll. De akkor az összes másodfokú ponthoz találtunk egy-egy legalább negyedfokú pontot. Így a második emeleten a fokszámok átlaga legalább három. A favázban viszont a második emelet minden pontja elsőfokú. Ha tehát a faváz éleit elhagyjuk, a kapott gráfban a második emelet pontjainak átlagfokszáma még mindig legalább kettő, s ez azt jelenti, hogy az élszám legalább annyi, ahány pont van a második emeleten: n–3. Ehhez hozzávéve a faváz éleit ismét legalább 2n–4 élet kapunk, s ezzel a bizonyítást befejeztük.
21. Egy körön nyilván megadható ilyen hozzárendelés: irányítjuk a kört és minden élhez a „későbbi” végpontját rendeljük.
Másrészt ha P=x1x2…xm egy út, akkor az xi→xixi+1 hozzárendelés minden ponthoz egy megfelelő élt rendel, csak a kezdőponthoz nem rendel semmit.
Általában minden fában megadható megfelelő hozzárendelés úgy, hogy csak a fa gyökeréhez nem rendelünk élt: minden ponthoz azt az élt rendeljük, amely a pontot az apjával köti össze.
Nyilván feltehetjük, hogy a gráfnak pontosan n éle van.
Egy n pontú és legalább n élű gráfban van kör. E körön adjuk meg a hozzárendelést, majd hagyjuk el a kör éleit a favázból. Így egy olyan erdőt kapunk, amelyben minden fakomponens gyökere a kör egy pontja, tehát van már hozzárendelt él. A fakomponens többi pontjához (ha van ilyen) pedig hozzárendelhetjük azt az élt, amely az apjával köti össze.
MEGJEGYZÉS: A megoldást elmondhattuk volna úgy is, hogy először vesszük a gráf egy feszítő fáját, és egy olyan xy élt, amely nincs benne a feszítő fában és ezt az élt megfeleltetjük x-nek. A fa bármely pontját tekinthetjük a fa gyökerének, legyen tehát a gyökér x. Az x gyökerű fában minden más ponthoz hozzárendeljük az őt az apjával összekötő élt. Így egy a feladat feltételét teljesítő hozzárendelést kapunk.
51. a) Tegyük fel indirekte, hogy minden y-hoz van két olyan részhalmaz, Fi és Fj, amely X–y-on nem megkülönböztethető. Ez csak úgy lehetséges, ha a két halmaz csak „y-ban különbözik”: Fi=Fj\{y} (vagy fordítva). Minden y-hoz kiválasztunk egy (és csak egy!, ennek később lesz jelentősége) ilyen Fi,Fj párt. Különböző y-hoz nyilván különböző Fi,Fj párok tartoznak. Tekintsük azt a H gráfot, amelynek pontjai az Fi halmazok és élei az ilyen FiFj párok. Írjuk is rá minden élre, hogy az X halmaz melyik y eleme „miatt” választottuk ki ezt az élt.
Az így kapott H gráfnak n pontja és n éle van: minden y elemhez pontosan egy él tartozik és különböző y-okhoz különböző élek tartoznak. A H gráfban tehát van egy E1E2…EkE1 kör. Ez a kör olyan, hogy bármely két szomszédos ponthoz tartozó halmaz csak egy elemben különbözik: éppen abban az elemben, amit az élre „írtunk”. Tekintsük azt az y elemet, amelyben E1 és E2 különbözik. Feltehető (a csúcsok esetleges átszámozása után), hogy E1=E2\{y}. Ekkor y nem eleme E3-nak, mert csak úgy lehetne eleme, ha E2 és E3 éppen y-ban különbözne, ami (itt használjuk ki, hogy minden y-hoz csak egy halmazpárt választottunk) lehetetlen. Ugyanígy lehetetlen az is, hogy valamelyik további Ei-nek eleme legyen y. Ha ugyanis Ei-nek eleme volna, de Ei–1-nek nem, akkor Ei és Ei–1 éppen y-ban különbözne, de (ismét használjuk, hogy minden y-hoz csak egy halmazpárt választottunk) ez lehetetlen. Így viszont oda jutunk, hogy E2, E3,…, En, E1 sem tartalmazza y-t, ami viszont E1 esetében ellentmondás. Ezzel bebizonyítottuk az állítást.
A b) rész pontosan ugyanígy bizonyítható, most az egyes sorok a gráf pontjai és két sort jelölő pont akkor van összekötve, ha pontosan egy elemben különböznek. Ha minden oszlophoz volna két sor, amelyek csak ebben az oszlopban álló helyen különböznek, akkor a gráfunkban volna kör, s arra megint elmondható volna az előző rész bizonyítása.
52. Nyilván nem változik a feladat, ha f(x,y) értéke az x és y közti összes séta közül a legkisebb súlyú séta súlya. Hagyjunk el a gráfból éleket mindaddig, amíg összefüggő marad és minden x,y csúcspárra f(x,y) értéke változatlan marad. Azt állítjuk, hogy az így kapott gráf fa. Ha ezt belátjuk, akkor kész vagyunk, hiszen f(x,y) csak e fa éleinek értékét veheti fel. – Tegyük fel, hogy van a gráfban egy C kör, és legyen C legnagyobb értékű éle e=ab. Ha ezt az élet elhagyjuk, akkor minden olyan x,y-ra változatlan marad f(x,y), amelyet összekötő legkisebb súlyú séta nem tartalmazza e-t. Ha viszont tartalmazza, akkor e helyettesíthető a C kör a és b közötti másik útjával. Ennek súlya nem nagyobb e értékénél, így a kapott séta súlya sem lesz nagyobb az eredeti sétáénál. Vagyis f(x,y) most sem nőtt (nyilván nem is csökkenhetett). e tehát elhagyható, amivel állításunkat igazoltuk: mindaddig hagyhatunk el a kívánt módon élt, amíg fához nem jutunk.
53. Megszámozzuk az éleket úgy, hogy minden legalább másodfokú ponthoz már két olyan él is legyen, amelyekre egymáshoz relatív prím számokat írunk (ez elég). Legyenek a gráf legalább másodfokú csúcsai A1,A2, …, An (ha n=0, akkor nincs mit biz.ni). Járjuk végig a következő ciklust: A1-ből elmegyünk A2-be, A2-ből A3-ba,…, An–1-ből An-be, majd An-ből A1-be a gráf egy-egy útján. Ilyen utak vannak, mert a gráf összefüggő. Ez a ciklus minden Ai-be bemegy egyszer, majd ki is jön egyszer. Sorra számozzuk az érintett éleket 1-gyel kezdve, és minden élt csak akkor számozunk meg, amikor az utazás során először érintjük, ekkor 1-gyel nagyobbat írunk rá, mint az utoljára használt szám. Arra kell vigyáznunk, hogy amikor egy csúcsba először megyünk be, akkor egy másik élen keresztül jöjjünk ki belőle, mint amin bementünk. Ez csak akkor nincs így, ha valamelyik Ai-be vezető út utolsó éléről van szó, és Ai-ből Ai+1-be ugyanezen az élen kellene elindulnunk. De ekkor van még legalább egy Ai-ből induló él (lehet, hogy ez később valamelyik úton még szerepelni fog, ez nem okoz gondot, csak az a lényeg, hogy eddig még nem szerepelhetett, mert most vagyunk először Ai-ben). Ezt az élt kétszer hozzávesszük a ciklushoz és először ezen megyünk tovább majd rögtön vissza is fordulunk, s csak ezután megyünk tovább az AiAi+1 úton. Nyilvánvaló, hogy így minden Ai-ből induló két élre két egymás utáni szám került, és az első l db számot használtuk el, ha a (esetleg bővített) ciklusban l él van. A többi élre az l+1, l+2, …, k számokat tetszőleges sorrendben ráírhatjuk.
54. Rajzoljuk be a (0,1) intervallumba az a/p és a b/q alakú pontokat (0<a<p és 0<b<q egész). Ez az intervallumot p+q–d részintervallumra osztja, s ha a tortát sorra olyan darabokra vágjuk, mint az egyes, így keletkezett intervallumok hossza, akkor nyilván egy megfelelő vágást kapunk p+q–d részre. Másrészt osszuk fel a tortát a feladat feltételeinek megfelelő módon. Tekintsük azt a páros gráfot, amelynek “fent” p pontja, “lent” q pontja van; a fenti pontok azok a halmazok, amelyeket az egyes vendégek kapnak, ha p egyenlő részre osztjuk a tortát, a lenti pontok azok a halmazok, amelyeket az egyes vendégek kapnak, ha q részre osztjuk a tortát. Két pont akkor van összekötve, ha a két halmaznak van közös eleme. (A felső i-edik pont és az alsó j-edik pont akkor van összekötve, ha az i-edik vendég a p-ből és a j-edik vendég a q-ból legalább egy azonos tortaszeletet kapna.) Ha d=1, akkor ez a gráf összefüggő. Ha ugyanis fentről a, lentről b pont alkot egy komponenst, akkor vegyük a pontoknak megfelelő a illetve b embert. Ez az a ember csak olyan tortarészeket kapna a p-es felosztásnál, amilyeneket a b másik kapna a q-as felosztásnál. Ez viszont azt jelenti, hogy az a embernek járó a/p rész és a b embernek járó b/q rész egyenlő. Vagyis aq=bp. Ha most p és q relatív prímek, akkor p|a>0 és q|b>0, vagyis a≥p és q≥b, tehát a=p, b=q, és ez pontosan azt jelenti, hogy a gráf összefüggő (csak egy komponensből áll). Ha viszont (p,q)=d, és p=dP, q=dQ, akkor P|a, Q|b, tehát a≥P=p/d, b≥Q=q/d, amiből viszont következik, hogy a gráf legfeljebb d komponensből áll, vagyis legalább p+q–d éle van. Ez azt jelenti, hogy legalább p+q–d részre vágtuk a tortát (minden él legalább egy tortaszeletet jelent, különböző élek különböző tortaszeletet jelentenek).
55. Ha e≤n–2, akkor G nem összefüggő, tehát e=n–1 vagy e=n. Ha e=n–1 és G összefüggő, akkor fa. Viszont fában mindig van elsőfokú pont. Marad az az eset, ha e=n. A G gráf összefüggő, ezért tekinthetjük egy favázát, legyen ez F. F-et G-ből egyetlen e él elhagyásával kapjuk, hiszen F-nek n–1 éle van. Láttuk, hogy egy legalább két pontú fában mindig van legalább két elsőfokú pont (39. feladat). Ha az e él nem ezt a két pontot köti össze, akkor ismét van elsőfokú pont a G gráfban. Tehát tudjuk, hogy e az F fa két elsőfokú pontját köti össze, és a fának nincs több elsőfokú pontja. Vagyis a G gráfnak minden pontja legalább másodfokú. De n éle csak úgy lehet, ha minden pontja pontosan másodfokú. Ekkor viszont minden komponense kör. Mivel egy komponense van, a gráf maga egy kör, és ezt akartuk bizonyítani.
56. Összefüggő gráfokban e≥n–1. Ha e=n–1, azaz a gráf fa, akkor nyilván egyetlen ilyen részgráf van, hiszen minden erdőben van elsőfokú pont, kivéve az üres gráfot. Ha e=n és a gráf összefüggő, akkor egy köre van (ld. a 23. feladatot). Ha ennek a körnek bármely élét elhagyjuk, akkor már egy legfeljebb n–1 élű gráfot kapunk, amelyről azt is tudjuk, hogy körmentes. Így minden komponense fa. Ha valamelyik komponense nem üres, azaz tartalmaz élt, akkor a 39. feladat szerint van benne (legalább két) elsőfokú pont, tehát az ilyen részgráf nem megfelelő. Vagyis ha a körből hagyunk el élt, akkor már a gráf minden élét el kell hagynunk, azaz ezesetben csak az üres gráf felel meg. Ha viszont olyan xy élt hagyunk el a gráfból, amely nincs benne körben, akkor a gráf több komponensre esik szét: x és y különböző komponensbe kerül, mert nem megy köztük út (ha menne, az az xy éllel együtt kört zárna be). A gráf egyetlen körét csak az egyik komponens tartalmazhatja, az összes többi komponens tehát fa. Ezek minden élét el kell hagynunk, mert különben nem-üres erdőt alkotnak, s abban van elsőfokú pont. Másrészt a kört tartalmazó komponensnek sem lehet a kör pontjain kívül pontja az előző feladat előző feladat szerint. Tehát e=n esetén két megfelelő részgráf van: az üres gráf és az a feszítő gráf, amelynek élei a gráf egyetlen körének élei.
Belátható az is, hogy ha e=n+1 és a gráf összefüggő, akkor a gráfnak négy megfelelő feszítő részgráfja van. Ebben az esetben ugyanis két lehetőség van: a gráfban vagy két éldiszjunkt kör van, vagy egy kör van átlóval. Az előbbi esetben a négy megfelelő feszítő részgráf: az üres gráf, az egyik kör éleiből álló feszítő részgráf, a másik kör éleiből álló feszítő részgráf és a két kör éleiből álló feszítő részgráf. A második esetben is négy megfelelő részgráf van: az üres gráf, az a gráf, amelyiket úgy kapunk, hogy elhagyjuk az átlót és minden olyan élt, amelyiknek van a körön kívüli végpontja, és valamint az a két részgráf, amelynek élei egy-egy olyan kör élei, amely tartalmazza az átlót; ilyenből pont kettő van.
Ha még megvizsgáljuk például a négypontú teljes gráfot, abban n=4, e=6 és az üres gráfon kívül megfelelőek azok a részgráfok, amelyek egy háromszög három éléből állnak, ilyen négy van, továbbá az olyanok, amelyek egy-egy négy hosszú kör négy éléből állnak, ilyen három van. Ez összesen nyolc megfelelő feszítő részgráf.
Az ötpontú teljes gráfnak megfelelő részgráfjai az üres gráf, a tíz háromszög, az 5·3=15 négyszög, a 12 ötszög, valamint azok, amelyekben van negyedfokú (telített) pont: ilyen maga a teljes gráf, ilyenek azok, amelyek két, egy pontban érintkező háromszögből állnak, ilyenből van 3·5=15, továbbá azok, amelyekben két telített pont van, a másik három pontja másodfokú, ilyenből tíz van. Ez összesen 64 megfelelő részgráf, ami 2e–n+1. Ugyanez a képlet jó az előzőleg tárgyalt esetekben is.
Az eddigi példák alapján megpróbálkozhatunk annak bizonyításával, hogy minden n pontú, de e élű összefüggő gráfnak 2e–n+1 megfelelő részgráfja van.
1. MEGOLDÁS (Maga Péter megoldása alapján): Az e=n–1, e=n esetekben már bebizonyítottuk az állítást. Ezután adott n mellett az élszámra alkalmazunk indukciót. Ha e>n, akkor van kör a gráfban, legyen e=xy olyan él, amely benne van valamely C körben (nem hídél). Ez a C kör lesz a „váltó”, ezt fogjuk átállítani a következőképpen. Tekintsük G egy tetszőleges H részgráfját, ehhez hozzárendelünk egy másik részgráfot úgy, hogy a C kör éleit „kicseréljük”: azokat az éleit, amelyek benne vannak H-ban, elhagyjuk belőle, azokat az éleit, amelyek nincsenek H-ban, hozzávesszük H-hoz. Így minden H-hoz hozzárendelünk egy H’-t. (A hozzárendelés H’-höz H-t rendeli.) Ezzel az eljárással a kör pontjainak fokszáma páros számmal változik (vagy változatlan marad, vagy kettővel nő, vagy kettővel csökken), a többi pont fokszáma nem változik, tehát ha H megfelelő volt, H’ is az; ha H nem volt megfelelő, akkor H’ sem az. Másrészt H és H’ közül pontosan az egyik tartalmazza az e élt, s ez a G–e gráfban nem részgráf. Vagyis a megfelelő részgráfoknak pontosan a fele megfelelő G–e-ben: azok, amelyek nem tartalmazzák az xy élt. G nem-megfelelő részgráfjai közül azok, amelyek nem tartalmazzák az e élt, G–e-ben sem megfelelők, azok pedig, amelyek tartalmazzák ezt az élt, nem is részgráfjai G–e-nek. Tehát G megfelelő részgráfjainak a száma G–e részgráfjai számának pont a kétszerese. Ezzel az indukciót befejeztük.
2. MEGOLDÁS. A gráf összefüggő, tehát vegyünk egy favázát. A favázban nem szereplő élek száma e–n+1. Válasszunk ki ezek közül az élek közül egy tetszőleges E’ részhalmazt. Megmutatjuk, hogy E’ élhalmaz a faváz éleivel egyértelműen egészíthető ki úgy egy E’’ élhalmazzá, hogy minden pont foka páros legyen. Vegyük először a faváz elsőfokú pontjait: ezekről egyértelműen dönthető el, hogy a belőlük induló élt hozzá kell-e venni E’’-hoz, vagy sem: ez csak attól függ, hogy az illető elsőfokú pont (legyen a) fokszáma az E’ élhalmazban páratlan-e (ekkor a fa a-ba érkező élét hozzávesszük E’-höz), vagy páros (ekkor a fa a-ba érkező élét nem vesszük hozzá E’-höz). Ezután elhagyjuk ezeket az elsőfokú pontokat a favázból és újra megkeressük a maradó faváz elsőfokú pontjait, azokra ismét alkalmazzuk az eljárást. Az eljárást addig ismételjük, amíg az elsőfokú pontok elhagyása után már nem marad él a favázból. Ezzel beláttuk, hogy az E’ élhalmaz élei egyértelműen egészíthetők ki a faváz éleivel egy megfelelő élhalmazzá. Ilyen E’ élhalmaz viszont pontosan 2e–n+1 van. Ennyi megfelelő részgráf van.
3. MEGOLDÁS (Hubai Tamás megoldása): Azt, hogy az E’ élhalmaz élei egyértelműen egészíthetők ki megfelelő E’’ élhalmazzá, bebizonyíthatjuk másképp is. Először megjegyzezzük, hogy ha F és F’ megfelelő élhalmaz (tehát a gráf minden pontjának páros a foka mindkettőben), akkor megfelelő élhalmaz a kettő szimmetrikus differenciája, az F∇F’ élhalmaz is (F és F’ uniójából elhagyjuk a közös éleket). Másrészt ismert, hogy a szimmetrikus differencia művelete kommutatív és asszociatív (k halmaz szimmetrikus differenciája pontosan azokat az elemeket tartalmazza, amelyek a k halmazból páratlan sokban vannak benne).
Nevezzük a faváz éleit 1-típusú éleknek, a favázból kimaradó éleket 2-típusú éleknek. Minden 2-típusú e élhez hozzárendelhetjük azt a Ce kört, amely e-n kívül csupa 1-típusú élből áll. Ilyen kör pontosan egy van, mert a favázban e két végpontja között pontosan egy út fut. Ce nyilván megfelelő élhalmaz. Legyen most E’ a 2-típusú élek halmazának egy tetszőleges részhalmaza, ehhez rendeljük hozzá azoknak a Ce élhalmazoknak a szimmetrikus differenciáját, amelyekre e benne van E’-ben. Az üres részhalmazhoz az üres gráfot rendeljük. Így E’ minden részhalmazához egy-egy megfelelő G’ részgráfot rendeltünk. Nézzük, melyik 2-típusú élek szerepelnek ennek élhalmazában. Minden 2-típusú e él eleme Ce-nek és nem eleme egyetlen más f élhez tartozó Cf körnek sem. Tehát a szimmetrikus differenciában e pontosan akkor van benne, ha Ce szerepel azok között a körök között, amelyek szimmetrikus differenciáját képeztük. Vagyis: a kapott G’ részhalmaz a 2-típusú élek közül pontosan E’ elemeit tartalmazza. Ebből már következik, hogy bármely két különböző E’-höz tartozó G’ is különböző. Ez pontosan 2e–n+1 megfelelő (feszítő) részgráf. Azt kell még belátnunk, hogy nincs más megfelelő részgráf. Tegyük fel, hogy van, legyen ez H. Legyen E’ azoknak a 2-típusú éleknek a halmaza, amelyek elemei H-nak. Tekintsük az E’-höz az előbb definiált G’ megfelelő részgráfot. Ekkor G’∇;H=L is megfelelő részgráf. Másrészt G’-nek is, H-nak is ugyanazok a 2-típusú élek az elemei: E’ elemei. Tehát ebben az L részgráfban nem szerepel egyetlen 2-típusú él sem, csak 1-típusú él. De azt már láttuk, hogy a faváz éleinek csak egy megfelelő részhalmaza van: az üres halmaz. Vagyis L az üres halmaz, ami azt jelenti, hogy G’ megegyezik H-val. Ez ellentmondás, vagyis valóban csak az előbb definiált 2e–n+1 megfelelő (feszítő) részgráfja van G-nek.
MEGJEGYZÉS (Rácz Béla András): A 2. megoldásban bizonyított állítást teljes indukció nélkül is beláthatjuk. Az állítás ugyanis a következő: ha egy G gráf fa, és minden pontjára ráírunk 0-t vagy 1-et úgy, hogy a pontokra számok összege páros legyen, akkor G-nek pontosan egy olyan feszítő részgráfja van, amelyben a 0-val jelölt pontok foka páros, az 1-gyel jelöltek foka páratlan. Ezt bebizonyíthatjuk a következőképpen is: ha G-nek n pontja van, akkor összesen 2n–1 olyan 0-1 sorozatot írhatunk a pontokra, amelyben az összeg páros. Másrészt G-nek n–1 éle, tehát pontosan ugyanennyi feszítő részgráfja is van. Elég tehát belátnunk, hogy minden feszítő részgráf különböző 0-1 sorozathoz tartozik, vagyis hogy ugyanahhoz a 0-1 sorozathoz nem tartozhat két különböző feszítő részgráf. Tegyük fel, hogy F és F’ két feszítő részgráf, amelyben minden pont fokának paritása megegyezik. Vegyük F és F’ élhalmazának szimmetrikus differenciáját, vagyis vegyük az uniójukat és hagyjuk el azokat az éleket, amelyek mindkettőben szerepelnek. Könnyen belátható, hogy így egy olyan feszítő részgráf élhalmazát kapjuk, amelyben minden pont foka páros. (Tetszőleges x pont fokának F-ben és F’-ben ugyanolyan volt a paritása, így a két fokszám összege páros. Ha k darab x-ből induló élt kellett elhagyni, mert mindkettőben szerepelt, akkor a fokszámösszeg 2k-val csökkent, tehát továbbra is páros maradt.) Márpedig G minden részgráfja erdő, tehát ha nem üres, akkor van elsőfokú pontja. Így F és F’ szimmetrikus differenciája csak az üreshalmaz lehet, ami pontosan azt jelenti, hogy F megegyezik F’-vel, és ezt akartuk bizonyítani.
57. a) Az I/16-ban alkalmazott megoldás nyomán haladunk. Válasszunk ki egy tetszőleges embert: ő és az ismerősei együtt mindenkit ismernek (most őrá is szükség van, mert akiket ismer, azokkal nem biztos, hogy van közös ismerőse). Ha tehát van a társaságnak olyan tagja, aki legfeljebb n-et ismer, akkor kész vagyunk.
Tegyük fel, hogy mindenkinek legalább n+1 ismerőse van. Most is kiválaszthatunk találomra valakit, az ő legalább n+1 ismerősével akkor már nincs gondunk. Marad még 2n–2 ember, ezeket kellene párba állítanunk úgy, hogy bármely párnak legyen közös ismerőse. Ha e 2n–2 ember között van kettő, akik nem ismeri egymást, akkor nekik van közös ismerősük, K1, válasszuk ki K1-et és hagyjuk el e két embert. A maradó 2n–4 ember közül megint keresünk kettőt, akik nem ismerik egymást, s megismételjük az eljárást, kiválasztjuk egy közös ismerősüket, K2-t. Addig választunk ki Ki embereket, amíg el nem akadunk. Az eljárás csak akkor akad el, ha néhány lépés után a maradó 2l ember között már nincs kettő, akik ne ismernék egymást, vagyis e 2l ember közül már mindenki mindenkit ismer. De akkor bármelyiküket kiválaszthatjuk, s ő már ismerni fogja a többit. Így tehát mindenképpen találunk legfeljebb n–1 további embert, akik együtt a maradék 2n–2-őt ismerik. Ebben az esetben tehát találtunk n embert, akik együtt mindenkit ismernek.
b) Könnyen ellenőrízhető, hogy amikor az I. fejezet 26. feladatánál azt bizonyítottuk, hogy mindig van 4n2/3 olyan ember, akik együtt mindenkit ismernek, valójában csak azt használtuk, hogy az ismeretség-gráf 2-átmérőjű.
58. Tekintsük a fa végpontjait (=elsőfokú pontjait): ezek mindegyikéhez kell egy új élet illesztenünk, különben nem mehet át rajtuk kör. Ha a fának k végpontja van, akkor ezek szerint legalább [(k+1)/2] új élt be kell húznunk ahhoz, hogy a fa minden pontján menjen át él.
Most a pontok számára vonatkozó teljes indukcióval megmutatjuk, hogy ennyi éllel mindig meg is oldható a feladat. Még valamivel többet is állítunk (így ugyanis könnyebben megy az indukció): megmutatjuk, hogy [(k+1)/2] él behúzásával már elérhető az is, hogy minden él is benne legyen körben. (Ez valóban több, hiszen például az alábbi gráfban minden pont benne van körben, de a vastagabban jelölt él hídél, nem megy át rajta kör: )

Még egy kicsit erősítjük állításunkat: az újonnan behúzandó élek mindegyike végpontokat köt össze. (Ha k páros, akkor a mondottak szerint nem is lehet másképp. Páratlan k esetén elképzelhető volna, hogy egy él egyik végpontja nem elsőfokú a fában, feltételünk ezt zárja ki.) Tehát a következő állítást fogjuk belátni:
Ha egy n pontú fának k elsőfokú pontja van, akkor az elsőfokú pontjai között behúzható [(k+1)/2] él úgy, hogy a kapott gráfban minden élen menjen át kör.
Állításunk könnyen igazolható, ha k=2, azaz a fának csak két végpontja van: ekkor a fa egy út, s ennek két végpontját összekötve egy olyan gráfot kapunk, amely egyetlen körből áll. A csillagra is könnyen igazolható az állítás: ha páros sok végpontja van, akkor párosítjuk a végpontokat és e párokat összekötjük, a kapott gráf egy pontban illeszkedő háromszögekből áll, minden él egy háromszögben van. Ha páratlan sok végpont van, akkor egy pont kimarad a párosításból, ezt egy tetszőleges végponttal összekötjük, így most is minden él benne van egy háromszögben.
Most megmutatjuk, hogy a kezdőlépésekre igaz az állítás: n=3 esetén csak egy fa van és ez út is, csillag is; n=4 esetén pedig csak két fa van: az út és a csillag.
Tegyük fel, hogy n>4 és n–2 és n–1 pontú fákra már beláttuk állításunkat és legyen G egy n pontú fa. Ha G-ben van másodfokú pont, akkor legyen x egy ilyen másodfokú pont, legyen két szomszédja y és y’. Hagyjuk el a fából x-et, és a belőle induló két élet, és kössük össze y-t y’-vel. Ez az él nem szerepelt G-ben, hiszen G-ben nincs kör. Másrészt a kapott G’ gráf továbbra is összefüggő és körmentes, tehát fa. Másrészt eggyel kevesebb pontja van, tehát alkalmazható indukciós feltevésünk. Végül még azt kell észrevennünk, hogy G’-nek ugyanazok a végpontjai, mint G-nek, tehát az indukciós feltevés szerint behúzható közöttük [(k+1)/2] él úgy, hogy a kapott gráf minden éle benne legyen körben. De akkor az yy’ él helyére visszaillesztve az yxy’ utat ez a tulajdonsága továbbra is megmarad: az a kör, amelyik yy’ élen ment keresztül, most keresztül fog menni yx és xy’ éleken, a többi élen pedig továbbra is fog keresztül menni kör.
A továbbiakban tehát feltehetjük, hogy a végpontokon (elsőfokú pontokon) kívül a fa minden pontjának foka legalább három. Azt is feltehetjük, hogy G nem csillag, mert ezt az esetet már elintéztük. Vegyük most a gráf egy leghosszabb útját, legyenek ennek végpontjai u és v, u szomszédja az úton u’, v szomszédja v’. Ha u nem volna elsőfokú pont a fában, akkor u’-től különböző u’’ szomszédja nem szerepelhetne az út pontjai között, hiszen ez esetben volna kör a fában. De akkor az uu’’ élt hozzáilleszthetnénk az úthoz, így nagyobb utat kapnánk, ami ellentmond feltevésünknek. Tehát u – s ugyanígy v is – elsőfokú. G nem csillag, ezért u’ és v’ különböző belső pontjai az útnak. De akkor u’ és v’ fokszáma legalább kettő, de feltevésünk szerint pontosan kettő nem lehet, ezért legalább három. Ha tehát u-t és v-t elhagyjuk a gráfból, nem keletkezik új elsőfokú pont, viszont két elsőfokúval kevesebb pont lesz. A fa pontszáma kettővel csökkent, tehát indukciós feltevésünk alkalmazható: a maradó k–2 elsőfokú pont között behúzható [(k–1)/2] él úgy, hogy a kapott gráfban minden élen menjen át kör. Ha most „visszatesszük” a gráfba az uu’ és vv’ éleket és u-t összekötjük v-vel, akkor egy olyan kört kapunk, amely keresztül megy uu’, uv, vv’ éleken is. Tehát minden élen megy keresztül kör. A behúzott élek száma eggyel nőtt, azaz éppen [(k+1)/2].
58.
I. MEGOLDÁS:
Nyilvánvaló, hogy ha egy gráfban van elsofokú pont, akkor az nem cutpoint. Az elsofokú pont bármely favázban is elsofokú lesz, tehát végpont lesz. Ha az összefüggo G gráfban nincs elsofokú pont, de találunk olyan x pontot, amely hasonlóan „végpont”-jellegu, akkor x elhagyásával nem fog „szétesni” a G gráf, így G-ben is van olyan pont, amely nem cutpoint. Erre már ismerünk egy módszert: vegyük a G gráf leghosszabb útját vagy azok közül egyet, legyen ez P, és legyen x a P út egyik végpontja. Tudjuk, hogy x minden szomszédja az úton van: ha például y olyan szomszédja volna x-nek, amely nincs rajta P-n, akkor P-t meghosszabbíthatnánk az xy éllel, tehát P nem volna leghosszabb út. Most belátjuk a következo
SEGÉDTÉTELt:
Megmutatjuk, hogy x pontosan akkor cutpoint, ha van két olyan szomszédja, u és v, amelyek között az uxv úton kívül nem megy út a gráfban.
Nyilvánvaló, hogy ha u és v két ilyen szomszédja x-nek, akkor x elhagyásával ok különbözo komponensekbe kerülnek, tehát a G–x gráf valóban nem összefüggo, x valóban cutpoint. Ha pedig x cutpoint, akkor G–x több komponensre esik szét, így lesz olyan y és z pont, amelyek között G–x-ben nem megy út. Másrészt G összefüggo, tehát G-ben megy közöttük út, jelöljük ezt R-rel. Az R út ezek szerint biztosan tartalmazza x-et. Legyen ezen az úton x két szomszédja u és v. Az R út tehát így néz ki: z…uxv…y. Ha u és v között a gráfban menne az uxv útvonaltól különbözo út, akkor azt beírva uxv helyett kapnánk egy olyan sétát z és y között, amely nem tartalmazza x-et. Vagyis y és z között lenne séta G–x-ben. De akkor út is lenne közöttük G–x-ben, ami ellentmond az y-ra és z-re tett kikötésünknek. Ezzel beláttuk, hogy u és v valóban olyan szomszédai x-nek, amelyek között uxv az egyetlen út G-ben.
Segédtételünkbol már következik, hogy x nem cutpoint. Láttuk ugyanis, hogy x minden szomszédja az úton van. De ebbol következik, hogy bármely két szomszédjához van olyan út, amely „elkerüli” x-et: tudniillik a P útnak az a szakasza, amely e két szomszédját összeköti. Ez viszont a segédtételünk szerint azt jelenti, hogy x nem lehet cutpoint. Ezzel beláttuk, hogy minden összefüggo gráfnak van olyan pontja, amely nem cutpoint.
II. MEGOLDÁS:
A faváz segítségével sokkal hamarabb is célhoz érhetünk:
Vegyük a gráf egy favázát és annak egy elsofokú (vég-)pontját. Ha ezt elhagyjuk a fából, a fa továbbra is összefüggo marad, s akkor az egész maradó gráf is nyilván összefüggo marad, hiszen van faváza.
MEGJEGYZÉS:
Mindkét bizonyítás rögtön azt is adja, hogy tetszoleges összefüggo gráfban legalább két pont van, amely nem cutpoint. Mindkét bizonyításból kijön az is, hogy pontosan akkor van csak két cutpoint, ha a gráf egyetlen útból áll (ha minden faváza egyetlen út).






















