b) Ha egy négypontú gráfban nincs sem telített pont, sem izolált pont, akkor minden pont foka egy vagy kettő. Három eset van:– Minden pont foka egy, ami csak úgy lehet, ha két, közös pont nélküli élből áll a gráf. Ez három lehetőség:
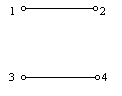
,
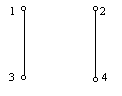
,
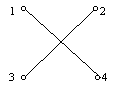
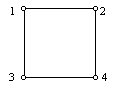
.– Minden pont foka kettő. Az ilyen gráfok komplementerében minden pont foka egy, tehát ilyenből is három van. Egyébként ezek a gráfok négy hosszú úgynevezett „körök”, például azutolsó gráf komplementere ilyen:
.– Két pont foka kettő, két pont foka egy (a gráf egy gráfelméleti „út”), a két első fokú pont egy-egy másodfokúval van összekötve és a két másodfokú egymással is össze van kötve:
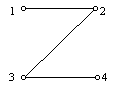
.A két elsőfokú pontot hatféleképpen választhatjuk, a maradó két pont sorrendjét pedig kétféleképpen, ez összesen 12 lehetőség.Összesen tehát 3+3+12=18 olyan négypontú gráf van, amelyben nincs telített pont és nincs izolált pont sem.