Ha az i pont telített a gráfban, akkor a gráf komplementerében izolált pont. Ezért az izolált pontot tartalmazó gráfok száma is Tn. Ezt fogjuk meghatározni. A logikai szitaformulát használjuk.Rögzítsünk k pontot a gráfban és tekintsük azokat a gráfokat, amelyekben ez a k pont izolált pont. Nyilvánvalóan annyi ilyen gráf van, ahány gráf van a maradó n–k ponton:
![]()
(lehetnek további izolált pontok is: ezért lesz szükség a logikai szitára). A k pontot
![]()
féleképpen választhatjuk ki. Ezért az izolált pontot tartalmazó gráfok száma a logikai szitaformula szerint:
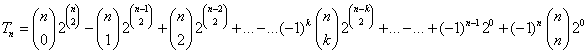
Itt az utolsó kettő kivételével minden tag páros. Az utolsó mindig páratlan (1), viszont az utolsó elotti paritása megegyezik n paritásával. Így Tn minden páros (pozitív egész) n-re páratlan, minden pozitív páratlan n-re páros.