Korábban ígértünk egy másik bizonyítást a II/2. feladatra, tehát arra, hogy bármely n pontú körmentes gráfban legfeljebb n–1 él van. Összefüggő körmentes gráfokra, azaz fákra már (E)-ben bebizonyítottuk, hogy pontosan ennyi éle van. Most egy új bizonyítást adunk az általános esetre, ami egyben pontosítja is 2. feladat állítását:
Ha a gráf nem összefüggő, akkor vegyük az összefüggő komponenseit, vagyis a legnagyobb összefüggő részgráfjait. Körmentes gráf minden részgráfja is körmentes. Így minden összefüggő komponense is körmentes, azaz fa. Ezért a körmentes gráfokat szokás erdőnek, vagy ligetnek is nevezni. (E) szerint egy ilyen erdő minden összefüggő részgráfjának a csúcsszámnál eggyel kevesebb éle van. Ebből kapjuk a következő tételt:
Egy körmentes gráf (azaz erdő vagy liget) élszáma egyenlő a csúcsok száma – az összefüggő komponensek száma.
(G)-ben láttuk, hogy minden összefüggő gráfnak van feszítő fája, így egy tetszőleges gráf minden összefüggő komponensének is van. Ebből viszont következik, hogy
(H) Ha egy gráfnak c darab komponense van, akkor van c fából álló feszítő erdeje. Ezért minden n pontú, c komponensből álló gráfnak legalább n – c éle van.
Abból a tényből, hogy összefüggő gráfnak van faváza, következett az (F) állítás, amely szerint összefüggő n pontú gráfnak legalább n–1 éle van. Az összefüggő komponens fogalmát használva erre is adhatunk egy új bizonyítást:
Hagyjuk el a gráf összes élét. Az így kapott üres gráf n komponensből áll. Most húzzuk be újra egyesével a gráf éleit. Nyilvánvaló, hogy minden él behúzása vagy eggyel csökkenti a komponensek számát (ha az él két különböző komponenst köt össze), vagy változatlanul hagyja (ha azonos komponenshez tartozó csúcsokat köt össze). Az eljárást addig folytatjuk, amíg a gráf összes élét be nem húzzuk. Végeredményben összefüggő gráfot kell kapnunk, vagyis olyan gráfot, amelyben a komponensek száma egy. Minden él behúzásánál maximum eggyel csökkent a komponensek száma és kezdetben n volt, ezért legalább n–1 élt kellett behúznunk.
MEGJEGYZÉS:
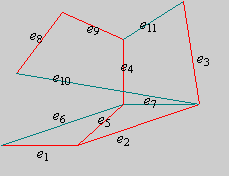
A bizonyításban ismertetett eljáráson csak kicsit kell változtatni ahhoz, hogy ez is a gráf egy favázát keresse meg, vagy általában is egy új algoritmust kapjunk összefüggő gráf feszítő fájának megkeresésére. Mindössze azt kell mondanunk, hogy ha egy él két eddig különböző komponens között fut, vagyis két komponenst egyesít, akkor kiválasztjuk a feszítő fába, ha azonos komponens pontjai között fut, akkor nem választjuk ki (hanem „szemétbe dobjuk”). Az ábrán zölddel jelöltük az elhagyott éleket, pirossal a kiválasztottakat. Az e1, e2, e3 élek egy hárompontú komponenst hoznak létre, e4 egy másik kétpontút. Az e5 él ezeket egyesíti, az e6 és e7 a kapott ötpontú komponensen belül fut, e8 egy új, kétpontú komponenst hoz létre, e9 ezt egyesíti az ötpontúval, végül e10 és e11 már „felesleges”, hiszen a piros élek már egy komponenssé egyesítették a gráf pontjait.
Ehhez az algoritmushoz olyan struktúrára van szükség, amely könnyen tudja kezelni, ha két komponenst egyesíteni kell, ugyanakkor gyorsan eldönthetővé teszi, hogy két pont azonos komponensben van-e, vagy különbözőben.
FÁK TOVÁBBI JELLEMZŐI
A most bebizonyított két tétel, amely szerint összefüggő n pontú gráfnak legalább n–1 éle van, körmentes n pontú gráfnak legfeljebb n–1 éle van, együtt ismét kiadja (E) állítás bizonyítását. Ez a gondolatmenet mutatja, hogy a fa egy úgynevezett „mini-max” tulajdonsággal bíró fogalom abban az értelemben, hogy egyszerre megoldása egy minimum- és egy maximum-kereső feladatnak. A körmentes gráfok közül ugyanis a fa élszáma a legnagyobb, míg az összefüggő gráfok közül a fáé a legkisebb. Ez magyarázza azt is, hogy miért játszik olyan fontos szerepet a gráfelméletben is, az algoritmuselméletben is.
Még egy féle módon kifejezhetjük azt, hogy a fának van egy minimum és egy maximum tulajdonsága is:
19. feladat:
Mutassuk meg, hogy ha G fa, akkor
a) bármely élét elhagyva megszűnik összefüggő lenni;
b) bármely új élt behúzva keletkezik benne kör;
c) egy tetszőleges x pontja pontosan akkor elsőfokú, ha G–x összefüggő.
