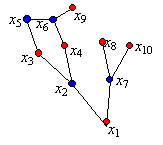
Nyilván elég az állítást összefüggő gráfokra vizsgálni, hiszen egy gráf pontosan akkor páros gráf, ha minden összefüggő komponense páros gráf. Legyen tehát G egy összefüggő gráf, amelyben minden kör hossza páros. Keressük meg egy feszítő fáját, például egy szélességi favázát. Színezzük ezt ki két színnel úgy, hogy a páros szintek pontjai (és a gyökér) pirosak legyenek, a páratlan szintek pontjai kékek. Ha sikerül a gráf pontjait két osztályba sorolni úgy, hogy csak különböző osztályok között menjen él, ez csak úgy lehetséges, ha a kék pontok alkotják az egyik osztályt, a pirosak a másikat. Ám a szélességi faváz bizonyított tulajdonsága szerint a gráf minden éle vagy azonos szintű pontok között fut, vagy szomszédos szintek között. A szomszédos szintek között futó élek „nem zavarnak”, mert különböző színű pontokat kötnek össze. Ha van olyan e=xy él, amely két azonos szintű pontot köt össze, akkor keressük meg x és y első közös osét, legyen ez u. Az x-bol u-ba vezető út és az y-ból u-ba vezető út egyforma hosszú és u-n kívül nincs közös pontjuk, hiszen u az első közös os. Ha a két utat összeillesztjük és az így kapott páros hosszú úthoz hozzávesszük az e élt, akkor egy páratlan kört kapunk. Ha ilyen él nincs, akkor viszont a fekete és a fehér pontok valóban két megfelelő osztályra bontják a gráf pontjait. (Az ábrán u=x5, v=x6, a közös os x2, a talált páratlan kör x5x3x2x4x6x5.)