Akár a szélességi faváz, akár a mélységi faváz (valójában bármely faváz) segítségével bebizonyítható egy fontos, a páros gráfokra vonatkozó tétel.
Mint emlékezetes, páros gráfnak az olyan gráfokat nevezzük, amelyeknek csúcsai két osztályba sorolhatók úgy, hogy a gráf minden éle különböző osztályba tartozó csúcsokat köt össze.

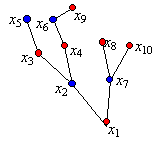
Minden fa páros gráf: a gyökeret rakjuk az első osztályba, az első szint pontjait a másodikba, majd általában a páros szintek pontjai kerülnek az első osztályba, a páratlan szinteké a másodikba. Ekkor nyilván nem fut él a két osztály között. Az ábrán pirossal és kékkel jelöltük a két szint pontjait. Általában is elmondhatjuk, hogy egy gráf pontosan akkor páros, ha csúcsai két színnel színezhetők úgy, hogy azonos színű pontok között ne fusson él.

Nyilvánvaló az is, hogy