A II/15 feladat megoldása, A MÉLYSÉGI KERESÉS

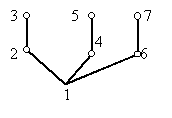
Egyáltalán nem magátólértetődő, hogy ilyen faváz mindig létezik. Persze, ha a gráf fa, akkor megfelel. Ha a gráf teljes, akkor bármely olyan út megfelel, amely tartalmazza a gráf összes pontját (az ilyen utat, ha van, a gráf Hamilton-útjának nevezzük). Érdemes ezt összevetni azzal, hogy milyen favázat ad a körkörösen haladó keresés ugyanennél a gráfnál. Itt egy csillagot kapunk, ami már sejtetni engedi, hogy mikor kaphatunk a második kérdés feltételét kielégítő favázat. Nyilvánvaló az is, hogy ha a gráfnak van Hamilton-útja, akkor ez az út megfelelő faváz. Általában is nyilvánvaló, hogy ha a gráfnak van Hamilton-útja, akkor bármely Hamilton-út megfelel a célunknak, ha egyik végpontja a gyökér. Hiszen egy ilyen Hamilton-útban bármely két pont közül az egyik a másik utódja. Vizsgáljunk meg még egy gráfot, amelyben három háromszög illeszkedik egy pontban:

Ha az 1-es pontot választjuk gyökérnek, akkor a szélességi faváz egy csillag lesz, s ez nyilván nem felel meg, hiszen a kimaradó élek mindegyike azonos szintű, tehát nem összehasonlítható pontok között fut. Nézzük, mi lehet jó. Nyilvánvaló, hogy például a 2-es és 3-as pont közül egyik az első emeletre, közvetlenül a gyökér fölé fog kerülni, feltehetjük, hogy a 2-es kerül az első emeletre. De akkor a 3-as pontnak a második emeletre kell kerülnie, különben az első emeletre kerülne, s akkor a 23 él nem előd és utód között futna. Hasonlóan a 4-es és 5-ös pont közül is az egyik az első emeletre kerül, a másik a másodikra, és a 6-os és 7-es pontra is ugyanez áll. A faváz most így néz ki:

Általában is világos, hogy ha a keresés során eljutunk egy xyz… út xy éléhez, tehát sorra került x és utána bevettük az xy élt is a fába, akkor z-t y utódjaként kell a fához illesztenünk. A legegyszerűbb az, ha y szomszédjaként vesszük sorra. Vagyis itt a szélességi („körkörös”) kereséssel ellentétben célszerű mindig „előre törni”. Olyan algoritmussal érdemes tehát próbálkoznunk, amelyik mindig előre megy, amíg ez lehetséges. Ha valahol elakadunk, akkor visszakozunk, de akkor is csak a lehető legkevesebbet, és onnan próbálunk meg előre törni új pontok felé. Ez lesz a mélységi keresés. Ha egy pontot elérünk, nem az összes szomszédja érdekel minket, hanem csak egy.

A III. ELJÁRÁS tehát a következő: Ha elérünk egy y ponthoz, keresünk egy olyan szomszédját, amelyet még egyetlen korábbi lépésben sem értünk el, ha van ilyen, ezt is felvesszük az elért pontok közé az y-ból hozzá vezető éllel együtt, és ez lesz az új y, majd ettől a ponttól folytatjuk a keresést. Akkor akadunk meg, ha olyan y ponthoz érünk, amelynek már minden szomszédját korábban elértük. Ekkor visszamegyünk ahhoz a ponthoz, ahonnan y-t elértük, és onnan próbálkozunk: ez (vagyis y fabeli „apja”) lesz az új y.

Az algoritmust ezzel megadtuk. Megadjuk valamivel formálisabban is:

1. LÉPÉS:
Kiválasztunk egy x₁ pontot, ez lesz a fa gyökere. Legyen y=x₁. (y változik az eljárás során!)

2. LÉPÉS:
Keressük meg y-nak egy szomszédját. Ha ilyen pont nincs, akkor az eljárást befejezzük (ekkor a gráf egy pontból állt).
Ha y-nak van szomszédja, válasszuk ki egy szomszédját, legyen ez x₂, a faváznak éle lesz az yx₂= x₁x₂ él és most y=x₂.

k. LÉPÉS:
Tegyük fel, hogy már kiválasztottuk az x₁,x₂,…,x_k–1 pontokat és y=x_i. Járjuk végig y szomszédait, amíg nem találunk olyat, ami még nem szerepel a kiválasztott x_j-k között.

1. eset: Ha y-nak van ilyen szomszédja (amely tehát még nem szerepel a kiválasztott x_j-k között), akkor az előszörre talált ilyen pont lesz x_k, a favázba beillesztjük az yx_k=x_ix_k éllel együtt és y=x_k.

2. eset: Ha y-nak minden szomszédja szerepel a kiválasztott x_j pontok között, akkor megkeressük y apját az x_j pontok között, ez lesz az új y, s erre ismételjük az eljárást. Egyetlen esetben nincs y-nak apja: ha y a gyökér. Az eljárás tehát akkor ér véget, ha visszaérünk a gyökérhez, és a gyökérnek már minden szomszédja szerepel a fában. Ekkor az eljárást befejezzük.

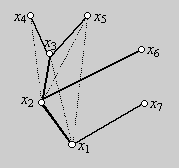
Az alábbi hatpontú gráfban a vastagon jelölt éleket a következő sorrendben húztuk be: x₁x₂, most y=x₂. A következő lépésben behúztuk az x₂x₃ élt és y=x₃, ezután behúztuk az x₃x₄ élt és y=x₄. Eddig „nyílegyenesen” haladtunk előre. A következő lépésben azonban y=x₄-bol csak visszafelé megy él (x₄x₂, ezt nem választjuk ki, az ábrán szaggatott), tehát y=x₃ és nem húzunk be élt. Az x₃x₁ él visszafelé megy, ezt nem húzzuk be (az ábrán szaggatott), viszont behúzzuk az x₃x₅ élt és y=x₅. Innen megint nem megy „előre” él csak visszafelé az x₅x₂ és x₅x₁ él (az ábrán szaggatott), ezért visszamegyünk x₅ apjához: y=x₃, innen sem tudunk már előbbre lépni, ezért y=x₂. Behúzhatjuk az x₂x₆ élt és y=x₆, innen már nem tudunk előrébb lépni, tehát ismét y=x₂ lesz, onnan sem mehetünk előrébb, tehát y=x₁. Most behúzzuk az x₁x₇ élt és y=x₇. Innen nem mehetünk előrébb, tehát ismét y=x₁ lesz, s onnan sem indul már új él, tehát az eljárásnak vége. A kiválasztott faélek vastagítva vannak, a többi él szaggatott.

Az eljárást ezzel megadtuk. A kérdés csak az, hogy a) valóban azt kapjuk, amit várunk tole: egy olyan favázat, amelybe a gráf összes éleit behúzva mindig elődöt és utódot fogunk összekötni; b) elég gyors-e ez az eljárás; és c) hogyan valósítható meg ez az eljárás számítógépen?

Először vizsgáljuk meg az a) és b) kérdést. Mindkét kérdésre igenlő a válasz, de egyik válasz sem magától értetődő. Ez az algoritmus is mohó, csakúgy, mint a szélességi keresés: mindkettő minden pillanatban a legkézenfekvőbbet teszi – csak mást tekint legkézenfekvőbbnek. A szélességi inkább védekező jellegű algoritmus, a mélységi inkább offenzív algoritmus. Mindkét esetben meg kell tehát vizsgálnunk, hogy ami adott pillanatban a legkézenfekvőbb, az végeredményben is a legjobb-e, vagy egyáltalán célhoz vezet-e.

Be kell tehát bizonyítanunk, hogy az ismertetett algoritmus véget ér, összefüggő gráf esetén valóban favázat ad és a kapott faváznak megvan a feladatban kívánt tulajdonsága. Ez azonban következik abból, hogy

MEGOLDÁS

Megjegyezzük, hogy az is igaz, hogy minden élt pontosan kétszer jár be: mindkét végpontjánál egyszer „találkozik” az éllel.

Az ismertett eljárásoknak az a tulajdonsága, hogy az összefüggő gráf minden pontját és élét bejárják, sok más, bonyolultabb algoritmusnál is szükségessé teszi oket!

MEGOLDÁS

MEGOLDÁS

A favázak, illetve a fenti kereső algoritmusok további fontos tudnivalókat is szolgáltatnak a gráfról:

1) Ha a keresés során egy már szereplő ponthoz jutnak vissza mint új szomszédhoz, ez pontosan azt jelenti, hogy a gráfban találtak egy kört.

2) Felmerül a kérdés, hogy mi történik, ha eljárásunkat egy nem összefüggő gráfra alkalmazzuk. A 15.a feladat megoldásánál láttuk, hogy az eljárásban sorra kerülő pontok együtt a gráf ponthalmazának egy olyan H részhalmazát adják, amelyből a) nem vezet ki él a sorra nem vett pontokhoz, b) a gyökérből H minden pontjába vezet út, tehát a H részhalmaz összefüggő részgráfot feszít a gráfban. E két tulajdonságot együtt úgy lehet összefoglalni, hogy H a gráf ponthalmazának egy tartalmazásra nézve maximális olyan részhalmaza, amely összefüggő részgráfot feszít. Röviden ezt úgy is szoktűk mondani, hogy H maximális összefüggő részhalmaza a gráfnak, vagy másképpen: H a gráf egy összefüggő komponense:

MEGOLDÁS

Ha a három (I., II., III.) eljárás közül bármelyiket tetszőleges gráfra futtatjuk, akkor bármely pontnak megtalálja az összefüggő komponensét. Ha pedig egy összefüggő komponenst megtalált, akkor ezt elhagyhatjuk a gráfból, s megismételhetjük az eljárást. Így pontosan annyi komponense van a gráfnak, ahányszor „újraindítjuk” az eljárást.

Mindhárom algoritmus alkalmas tehát arra is, hogy eldöntse adott gráfról, hogy összefüggo-e. A gráf pontosan akkor összefüggő, ha nem kell újraindítani az eljárást.

Az eljárások általános esetben egy feszítő erdőt adnak, amely a gráf minden komponensében egy-egy favázat ad meg.

MEGOLDÁS