Tegyük fel eloször, hogy az I. eljárásban xk-t mindig úgy választjuk, hogy a lehető legkisebb indexű kiválasztott ponttal legyen összekötve. Másképp fogalmazva ez a következőt jelenti:
II. ELJÁRÁS (szélességi faváz keresése összefüggő gráfban):
1. LÉPÉS:
Kiválasztjuk x1-et, ez lesz a fa gyökere, és ezt tekintjük a fa első szintjének.
2. LÉPÉS:
Ha nincs több pontja a gráfnak, az eljárást befejezzük.
Ha van még pont a gráfban, akkor x1-nek vannak szomszédai, mert a gráf összefüggő. Kiválasztjuk x1 szomszédait – ez lesz az első szint. Behúzzuk a második szint pontjait a gyökérrel összekötő éleket.
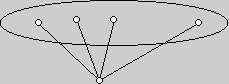
3. LÉPÉS:
Ha a gráfnak már minden pontját kiválasztottuk, akkor az eljárást befejezzük.
Ha nem minden pontot választottunk még ki, akkor (D) állítás szerint a kiválasztott pontok és a még ki nem választott pontok között fut él, mert a gráf összefüggő.
Végigmegyünk az első szint pontjain, és mindegyiknek kiválasztjuk azokat a szomszédait, amelyek még nincsenek kiválasztva. Ezek alkotják a második szintet. A második szint a fent mondottak szerint nem üres. A második szinten azok a pontok vannak, amelyeknek van szomszédja az első szinten, minden második szintű pontot összekötünk egy első szintű szomszédjával (például azzal, „amelyik miatt” kiválasztottuk).
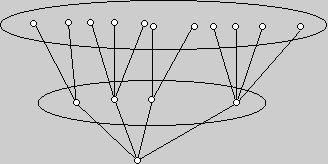
k. LÉPÉS:
Ha a gráfnak már minden pontját kiválasztottuk, akkor az eljárást befejezzük.
Ha nem minden pontot választottunk még ki, akkor (D) állítás szerint a kiválasztott pontok és a még ki nem választott pontok között fut él, mert a gráf összefüggő.
Általában a k+1-edik szintet azok a pontok alkotják, amelyek az k-adik szinten levő pontok szomszédai és még nem szerepelnek valamelyik korábbi szinten. A k+1-edik szint a fent mondottak szerint nem üres. Ezen a szinten azok a pontok vannak, amelyeknek van szomszédja az eloző, k-adik szinten, minden k+1-edik szintű pontot összekötünk egy k-adik szintű szomszédjával (például azzal, „amelyik miatt” kiválasztottuk).
Az eljárás akkor ér véget, amikor a gráf minden pontját besoroltuk valamelyik emeletre.