A feladat állítását teljes indukcióval bizonyítjuk.
n=1 esetén a gráfnak nincs éle, n=2 esetén a gráfnak legfeljebb egy éle van.
Tegyük fel, hogy n–1 pontú gráfokra már tudjuk az állítást és legyen G egy n pontú egyszerű, körmentes gráf. Az 1’ állítás szerint G-ben van egy legfeljebb elsőfokú pont (különben G nem körmentes), legyen ez a pont x. Hagyjuk el a G gráfból az x pontot és a belőle (esetleg) induló élt.
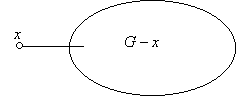
A maradó n–1 pontú gráfban továbbra sincs kör, így legfeljebb n–2 éle van az indukciós feltevés szerint. Ha ehhez hozzávesszük az x-ből induló egyetlen élt (ha van egyáltalán), megkapjuk, hogy G-nek legfeljebb n–1 éle van.