(B) ÁLLÍTÁSAINAK BIZONYÍTÁSA:
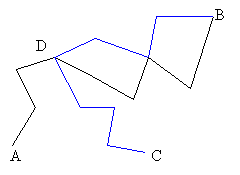
Az első állításhoz elég meggondolnunk, hogy a két pont közötti legrövidebb sétában nem lehet pontismétlődés, hiszen ha egy pontot többször is érintenénk, akkor a két érintése közötti részt nyugodtan elhagyhatnánk a sétánkból, s továbbra is a két pont közötti sétát kapnánk. (Az ábrán – ahol az élek sorrendjét számozással jelöltük – a kékkel jelölt „hurok” például elhagyható, de a többi él már nem.) Beláttuk tehát, hogy ha két pont között van séta, akkor a legrövidebb séta egyben út is.
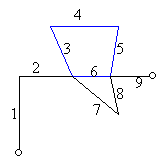
Valójában egy kicsit többet is beláttunk. Legyen a két végpont A és B és vegyünk egy tetszőleges sétát e két pont között. Ha tekintjük azokat a sétákat A és B között, amelyek csak ennek a sétának az éleit tartalmazzák, és kiválasztjuk közülük a legrövidebbet, már az is biztosan út. Ugyanis a fenti eljárással mindaddig hagyhatunk el az eredeti sétából „hurkot”, amíg megszűnnek a pontismétlődések.
Ebből a megjegyzésből viszont már következik (B) második állítása: tekintsük azt a sétát A és C között, amelyet az A-t B-vel összekötő útból, majd a B-t C-vel összekötő útból teszünk össze. Az előbb mondottak szerint A és C közötti út lesz a legrövidebb olyan séta, amely csak ennek a sétának az éleiből áll (tehát csak a két út éleit „használja”).
A második állítás bizonyítására bemutatunk egy másik bizonyítást is, amely egyrészt nagyon hasonlít az előző bizonyításra, másrészt nagyon hasonló a 3. feladat bizonyításához is. Induljunk el az A-ból B-be vezető úton és menjünk addig, amíg az első olyan ponthoz nem érünk, amely rajta van a B-t C-vel összekötő úton is. (Legkésőbb a B pont ilyen lesz.) Ebből a pontból folytassuk az utunkat a B-bol C-be vezető úton C-ig. Útközben biztosan nem találkozunk már érintett ponttal, hiszen D volt az első közös pont. Így kaptunk egy A-t C-vel összekötő utat.