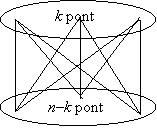
40.          Ha egy gráfban nincs páratlan kör, akkor a gráf a 18. feladat után adott jellemzés szerint páros gráf, vagyis pontjai két osztályba sorolhatók úgy, hogy a gráf minden éle a két osztály között fut. Ha az egyik osztályban k pont van, akkor a másik osztályban n–k pont van, így a gráfban maximálisan k(n–k) él van: ha a két osztály között minden él be van húzva. A számtani és mértani közép közötti egyenlőtlenség szerint k(n–k)≤n²/4. Ha n páros, akkor ez a pontos érték: k=n/2 esetén (tehát ha mindkét osztályban n/2 pont van) az élek száma pontosan n²/4. Ha viszont n páratlan, akkor n²/4 nem egész, tehát a nála kisebb legnagyobb egész, (n²–1)/4 a maximális élszám. Ez akkor lép fel, ha az egyik osztályban (n–1)/2 él van, a másikban (n+1)/2.