49. feladat megoldása

49. a) Ha egy gráf 2-átmérőjű, akkor összefüggő, tehát n pont esetén legalább n1 éle van. Másrészt a csillag olyan 2-átmérőjű n pontú gráf, amelynek pontosan n1 éle van. Tehát a minimális élszám n1. Könnyen belátható az is, hogy más 2-átmérőjű fa nincs, ez következik b)-ből:

b) Ha x elsőfokú és y a(z egyetlen) szomszédja, akkor y minden más ponttal is össze van kötve, mert ha egy z ponttal nem lenne összekötve, akkor x-nek és z-nek nem volna közös szomszédja, tehát x és z távolsága nem lehetne 2, azaz a gráf nem volna 2-átmérőjű. Az állítás tehát igaz: Ha egy 2-átmérőjű gráfban van elsőfokú pont, akkor annak szomszédja telített pont.

Ennek alapján már könnyen belátható, hogy az n pontú, n1 élű gráfok közül csak a csillag 2-átmérőjű: egy n pontú, n1 élű összefüggő gráf fa, tehát van elsőfokú pontja, s annak szomszédja telített pont. Tehát valóban csillagról van szó.

c) Hárompontú 2-átmérőjű gráf csak kettő van: a két élből álló út és a teljes hármas. Mindkettőben van telített pont, tehát hárompontú 2-átmérőjű gráfban van telített pont.

Ha egy négypontú 2-átmérőjű gráfban nincs telített pont, akkor minden pont foka legfeljebb kettő. Másrészt elsőfokú pont sem lehet benne b) szerint. (Izolált pont pedig nem lehet benne az összefüggőség miatt.) Tehát minden pont foka kettő. Ilyen négypontú gráf csak egy van: a négy hosszú kör.

Ha egy ötpontú 2-átmérőjű gráfban nincs telített pont, akkor minden pont foka legfeljebb három. Másrészt nincs benne izolált pont és nincs benne elsőfokú pont sem b) szerint. Tehát minden pont foka 2 vagy 3. Nem lehet minden pont foka 3, hiszen páros sok páratlan fokú pontja van (lásd az I. fejezet 20. feladatát). Tehát van egy másodfokú pontja. Azt is tudjuk, hogy vagy egy vagy három másodfokú pontja van, vagy minden pontja másodfokú. Az utóbbi esetben egy öt hosszú körről van szó, amely valóban 2-átmérőjű (!). Ha csak egy másodfokú pont van, legyen ez x és legyen két szomszédja y és z és legyen u és v a két további pont. Ezek csak úgy lehetnek harmadfokúak, ha össze vannak kötve y-nal is, z-vel is és egymással is, hiszen x-szel nincsenek összekötve. A következő gráfot kaptuk:

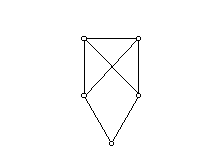
Ezt a gráfot leírhatjuk úgy, hogy ötszög két metsző átlóval. Végül ha három másodfokú és két harmadfokú pont van, akkor két eset lehetséges: ha a két harmadfokú pont van összekötve, akkor az összekötő élt elhagyva egy 2-reguláris gráfot kapunk, s ez öt pont esetén csak az ötszög lehet, tehát az így kapott gráf az ötszög egy átlóval. Ha viszont a két harmadfokú pont nincs egymással összekötve, akkor a következő gráfot kapjuk:

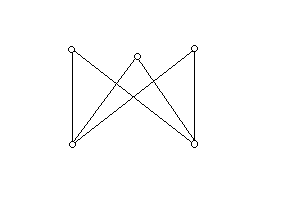
Ez a 2+3 pontú teljes páros gráf.

Végeredményben a következő ötpontú, 2-átmérőjű, telített pont nélküli gráfokat találtuk: az ötszög, az ötszög egy átlóval, az ötszög két egymást metsző átlóval és a 2+3 pontú teljes páros gráf.

d) A páros gráf csak úgy lehet 2-átmérőjű, ha bármely két, különböző osztályba tartozó pont össze van kötve. Ha ugyanis az x és y pont különböző osztályba tartozik, akkor nem lehet kettő hosszú úttal összekötve (és semmilyen páros élhosszú úttal sem lehet összekötve). Vagyis csak a teljes páros gráfoknak 2 az átmérője. Azok viszont nyilvánvalóan 2-átmérőjűek.

e) Ha egy körnek legalább hat pontja van, akkor van két olyan pontja, amely a kör mentén mindkét irányban legalább három távolságra van. Ha a gráfnak nincs további éle, akkor nem lehet 2-átmérőjű. Tehát csak a három-, négy- és ötpontú kör 2-átmérőjű.

f) A b) rész szerint a gráfban nem lehet elsőfokú pont. Legyen x egy minimális fokú pont a gráfban és legyen a fokszáma k, k≥2. Ha minden pont foka legalább három, akkor a gráfnak legalább 3n/2 éle van, nincs mit bizonyítanunk. Feltehetjük tehát, hogy k=2. A 29. feladat szerint az x gyökerű szélességi faváznak két emelete van. Az első emeleten van x két szomszédja, a második emeleten vannak x másodszomszédai, ez további n3 pont. A szélességi faváznak n1 éle van, a második szinten levő n3 pont legalább másodfokú, viszont a favázban elsőfokú, tehát a gráfban mindegyik ilyen pontból indul ki legalább még egy él. Ez összesen legalább (n3)/2 további él.

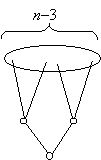
A gráfnak tehát legalább n1+(n3)/2=(3n5)/2 éle van, s ezt akartuk bizonyítani.

g) A c) részben talált 2+3 pontú teljes páros gráf mintájára könnyen találunk olyan 2-átmérőjű, telített pont nélküli gráfot, amelynek n pontja és 2n4 éle van: ilyen a 2+(n2) pontú teljes páros gráf, azaz az a páros gráf, amelynek egyik osztályában két pont van, a másikban n2 pont és a különböző osztályba tartozó pontok között minden él be van húzva. De kérdés, hogy nincs-e ennél kevesebb élű is? A c) részben láttuk, hogy n=4-re nincs, de n=5-re van: az ötszög. A 2+n2 pontú teljes gráf megkapható úgy is, hogy veszünk egy kettő hosszú xuy utat ez 2 átmérőjű gráf! , és középső pontját, u-t megsokszorozzuk, azaz felveszünk még n3 pontot és azt is összekötjük az út két végpontjával, x-szel és y-nal. Általában is igaz, hogy ha egy 2-átmérőjű gráfban van egy u másodfokú pont, akkor azt ily módon megsokszorozhatjuk, vagyis: ha felveszünk további pontokat, amelyeket összekötünk u két szomszédjával, akkor ismét 2-átmérőjű gráfot kapunk. Hiszen ha u-ból bármely pontba el lehetett jutni legfeljebb kettő hosszú úttal, akkor az újonnan felvett pontokból is el lehet jutni bármely régi pontba. Másrészt bármely két új pont között is van kettő hosszú út.

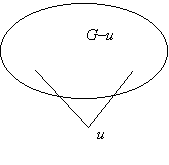
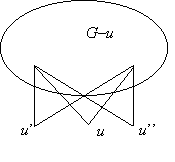
(Természetesen az állítás akkor is igaz marad, ha u fokszámáról nem mondunk semmit, és az új pontokat u összes szomszédjával összekötjük.) Ezzel viszont beláttuk, hogy akármilyen n≥5-re van olyan n pontú, telített pont nélküli 2-átmérőjű gráf, amelynek 2n5 éle van, s ezt az ötszögből kaphatjuk úgy, hogy valamelyik pontját megsokszorozzuk (vagy akár két másodszomszéd pontját is megsokszorozhatjuk):

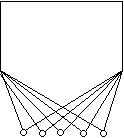
h) Ezek után a pontszámra vonatkozó teljes indukcióval belátjuk, hogy ha n≥5, akkor egy n pontú, 2-átmérőjű, telített pont nélküli gráfnak legalább 2n5 éle van. n=5-re már c)-ben beláttuk ezt.

A f) részhez hasonlóan most is induljunk ki egy minimális fokú pontból, legyen ez x és legyen x fokszáma k. Most is tudjuk, hogy k≥2. Másrészt ha minden pont fokszáma legalább négy, akkor a gráfnak legalább 2n éle van, tehát nincs mit bizonyítanunk. Ezek szerint k=2 vagy 3. Tekintsünk egy x gyökerű szélességi favázat. Legyen először k=3.

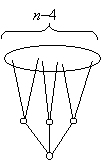
Az első emeleten ekkor három pont lesz, a második emeleten van a további n4 pont. A favázban ezek mindegyike elsőfokú, a gráfban viszont legalább harmadfokú, tehát mindegyikből indul ki további legalább két-két él. Ez összesen még legalább további n4 él, a faváznak n1 éle van, vagyis a gráfnak legalább n1+n4=2n5 éle van.

Marad az az eset, ha k=2. Ekkor az első emeleten van x két szomszédja, a második emeleten vanak x másodszomszédai, ez most n3 pont.

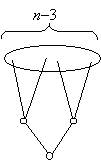
Hagyjuk el a faváz éleit, ez n1 élt jelent. Azt kell belátnunk, hogy legalább n4 él marad. Elég tehát belátnunk, hogy a második szinten levő pontok fokszámösszege a faváz éleinek elhagyása után 2(n4).

Tudjuk, hogy a gráf minden pontja eredetileg legalább másodfokú, tehát a második szinten a faváz éleinek elhagyása után minden pont legalább elsőfokú. Ha legfeljebb két elsőfokú van (tehát a gráfban legfeljebb két másodfokú pont van ezen a szinten), akkor a második emeleti pontok fokszám összege legalább 2+2(n5)=2(n4), amit bizonyítanunk kell.

Marad az az eset, ha a második szinten legalább három másodfokú pont van. Ebben az esetben kicsit pontosabban kell számolnunk. Használni fogjuk az indukciós feltevést is, éspedig olyan formában, hogy elhagyunk egy pontot a gráfból. Nyilván célszerű a legkisebb fokú pontot elhagyni, tehát egy másodfokú pontot. Ha az elhagyásával keletkező gráfban fennállnak az indukciós feltevés használásához szükséges feltevések, akkor e gráfban legalább 2(n1)5=2n7 él van, s ha ehhez hozzávesszük az elhagyott két élt, akkor az eredeti gráfban legfeljebb 2n5 él van, s ezt akarjuk bizonyítani.

Nézzük tehát először, hogy a másodfokú x pont elhagyása után keletkezhet-e telített pont a G\x gráfban.

Tegyük fel, hogy keletkezett egy t telített pont. Ez a t nem lehet az x pont valamelyik szomszédja (azaz nem lehet az x gyökerű szélességi faváz első emeletén), mert akkor t a G gráfban is telített pont volna, lévén, hogy x-szel is össze van kötve. Ha a második emeleten van, akkor a faváz éleinek elhagyása után is marad legalább n3 (t-ből induló) él, hiszen t G-ben n2-ed fokú és a favázban elsőfokú. Ez esetben a G gráfban legalább 2n4 él van, s ez több, mint amit bizonyítani akarunk.

Azt kaptuk, hogy G\x-ben nincs telített pont. Ha tehát G\x 2-átmérőjű, akkor alkalmazhatjuk az indukciós feltevést, és kész vagyunk.

Minthogy x tetszőleges másodfokú pont volt G-ben, a továbbiakban feltehetjük, hogy ha z másodfokú, akkor a G\z gráf nem 2-átmérőjű. Ám ha z két szomszédjának volna egy további z közös szomszédja, vagy két szomszédja össze lenne kötve, akkor G\z 2-átmérőjű volna:

Legyen ugyanis u és v a G\z gráf két, éllel össze nem kötött pontja. A G gráf 2-átmérőjű, tehát van a gráfban kettő hosszú uyv út. Ha y≠z, akkor ez az út benne van a G\z gráfban is. Ha viszont y=z, akkor u és v az z pont két szomszédja. De ekkor az első esetben uzv is út és benne van G\z-ben is, a második esetben uv 1 hosszú út G\z-ben. Azt kaptuk, hogy ha u és v G\z gráf két, éllel össze nem kötött pontja, akkor van közöttük egy vagy kettő hosszú út G\z-ben. Ez pontosan azt jelenti, hogy G\z valóban 2-átmérőjű vagy esetleg 1-átmérőjű!

A továbbiakban tehát feltehetjük, hogy ha z másodfokú, akkor két szomszédja között nem fut él és két szomszédjának nincs több közös szomszédja.

Legyen tehát x egy másodfokú pont. Ha felrajzoljuk az x gyökerű szélességi fát, és u-val és v-vel jelöljük x két szomszédját, akkor az aláhúzott állítás szerint u-nak és v-nek x-en kívül nincs közös szomszédja, és uv nem éle a gráfnak. Jelöljük U-val, illetve V-vel az u, illetve v pont x-től különböző szomszédainak halmazát. Ezek egyike sem lehet üres, mert ha például U üres volna, akkor u elsőfokú volna, ami c) szerint maga után vonná, hogy G-ben van telített pont. Szintén az aláhúzott állításból következik, hogy u nincs összekötve V pontjaival, v nincs összekötve U pontjaival:

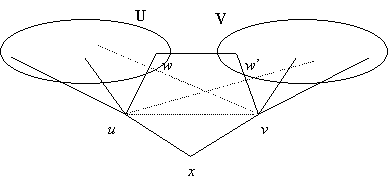
Ezután térjünk vissza oda, hogy a faváz második emeletén van legalább három másodfokú pont, legyen ezek egyike w∈U. Az aláhúzott állítás szerint w másik szomszédja nem lehet U-ban, de nem lehet v és x sem, vagyis w másik szomszédja V-ben van, jelöljük ezt w-vel. Ahhoz, hogy w-ből el lehessen jutni kettő hosszú úttal V minden pontjába, w-nek össze kell kötve lennie V minden pontjával, hiszen w másik szomszédja, u egyikkel sincs összekötve.