Árki Tamás és Hraskó András
Kísérletező geometria
Készült a Közoktatási Modernizációs Közalapítvány (KOMA) támogatásával
A kiválasztott feladatok
szv00702 feladatAdott háromszög mindhárom oldalegyenesét érintő
kardioidok (a szóbajövő kardioidokról
tehát nem kötjük ki, hogy azonos legyen a tengelyirányuk)
centrumainak mértani helye kilenc egyenes egyesítése. E kilenc egyenes
egyenlete (lásd az szv00603 feladatot):
ahol
Δ1,
Δ2,
Δ3
a tekintetbe vett pont (a
kardioid centruma) és az e1, e2, e3
egyenesek előjeles távolságát jelöli, a pozitív előjelet a háromszögtartomány
felőli félsíkban értve, míg Δ’1,
Δ’2, Δ’3 a háromszög Δ1
, Δ2, Δ3 külső szögeivel egyezik meg
mod 360° és összegük 0°.
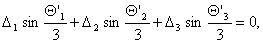 |
|
szv00702_fel_a. egyenlet
|
Előzetes megjegyzés, segítség, megoldás és folytatási javaslat kérése