Árki Tamás és Hraskó András

Kísérletező geometria

Készült a Közoktatási Modernizációs Közalapítvány (KOMA) támogatásával

Főoldal Órák Feladatok Cikkek Fejlesztőknek

A(z) szv005 kódszámú óra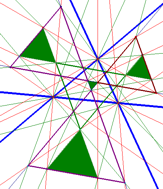
Javasolt évfolyam:11-12.
Segédeszköz:Papír, ceruza, tábla, kréta,
Előző óra:szv004 óra
Következő óra:szv006 óra

Feladatok

szv00501 feladatMódosítunk az szv00201 feladaton. Guruljon most egy rögzített e kör körül egy feleakkora sugarú k kör. A k kör valamely pontja által leírt görbét nefroidnak (vesegörbe) nevezik.
a) Ábrázoljuk a nefroidot!
b) Határozzuk meg a nefroid valamely pontjában az érintőegyenest úgy, ahogy azt a kardioiddal kapcsolatban az szv00401 feladatban tettük!
c) Mutassuk meg, hogy a párhuzamos fénysugarak egy félkör belső felületén való tükröződés után egy nefroidot érintenek (tehát nefroidot látunk a teáscsészében).
szv00600 feladat

Ezt a feladatot dinamikus geometriai szoftverrel oldjuk meg!

a) Vegyünk fel egy háromszöget, rajzoljuk meg a szögharmadolóit, jelöljük be a szögharmadolók egymással alkotott metszéspontjait! Tegyünk megfigyelést, fogalmazzunk meg sejtést! A csúcsok mozgatásával "ellenőrizzük" a sejtés helyességét!

szv00600_fel_a. ábra.

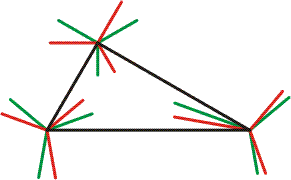
b) Rajzoljuk meg az össze szögharmadolót, azaz az előbbiek 120°-os elforgatottjait, és tegyünk további megfigyeléseket!

szv00600_fel_b. ábra.

Előzetes megjegyzés, segítség, megoldás és folytatási javaslat kérése

  Előzetes megj. Segítség Megoldás Folytatás
szv00501. feladat (0) (0) (1) (0)
szv00600. feladat (0) (0) (1) (3)

Házi feladatok

szv00601 feladatMutassuk meg, hogy a kardioid OA szimmetriatengelyével θ szöget bezáró érintőn az érintési pont a kardioid O középpontjától
távolságra van, ahol r = OA, és az A pont a kardioid szinguláris pontja.
szv00602 feladatIgazoljuk a
sinα sin(γ - β) + sinβ sin(α - γ) + sing sin(β - α) = 0
azonosságot!
szv00604 feladat

Ez a feladat az egyenes egyenletéről szól a komplex számsíkon. Mutassuk meg, hogy a z komplex szám pontosan akkor illeszkedik az

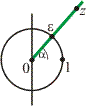
a) origón és az ε egységnyi abszolút értékű komplex számon átmenő egyenes­re, ha

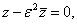
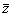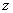ahol  a  komplex szám konjugáltját jelöli.

szv00604_fel_a. ábra.

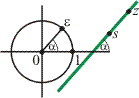
b) s komplex számon átmenő, a valós tengellyel az ε komplex egység argumentumával egyenlő szöget bezáró egyenesre, ha

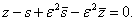
szv00604_fel_b. ábra.

Előzetes megjegyzés, segítség, megoldás és folytatási javaslat kérése

  Előzetes megj. Segítség Megoldás Folytatás
szv00601. feladat (0) (0) (1) (2)
szv00602. feladat (0) (0) (1) (1)
szv00604. feladat (0) (0) (1) (1)