Árki Tamás és Hraskó András
Kísérletező geometria
Készült a Közoktatási Modernizációs Közalapítvány (KOMA) támogatásával
| A(z) szv007 kódszámú óra |  | |
| Javasolt évfolyam: | 11-12. | |
| Segédeszköz: | Papír, ceruza, tábla, kréta, | |
| Előző óra: | szv006 óra | |
Feladatok
szv00701 feladatHa az O centrumú kardioid szinguláris pontja A
és a kardioid érinti az E1E2E3
háromszög E2E3=e1, E3E1=e2,
E1E2=e3 oldalegyeneseit,
akkor
ahol
Θ1,
Θ2,
Θ3
az e1, e2,
e3 egyeneseknek a kardioid OA tengelyével bezárt
szögét (lásd az szv00401 feladat 1.
megoldásához fűzött 1.megjegyzést),
Δ1, Δ2, Δ3
pedig O és az e1,
e2, e3 egyenesek (előjeles) távolságát
jelöli.
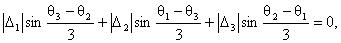 |
|
szv00701_fel_a. egyenlet
|
szv00702 feladatAdott háromszög mindhárom oldalegyenesét érintő
kardioidok (a szóbajövő kardioidokról
tehát nem kötjük ki, hogy azonos legyen a tengelyirányuk)
centrumainak mértani helye kilenc egyenes egyesítése. E kilenc egyenes
egyenlete (lásd az szv00603 feladatot):
ahol
Δ1,
Δ2,
Δ3
a tekintetbe vett pont (a
kardioid centruma) és az e1, e2, e3
egyenesek előjeles távolságát jelöli, a pozitív előjelet a háromszögtartomány
felőli félsíkban értve, míg Δ’1,
Δ’2, Δ’3 a háromszög Δ1
, Δ2, Δ3 külső szögeivel egyezik meg
mod 360° és összegük 0°.
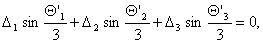 |
|
szv00702_fel_a. egyenlet
|
szv00703 feladatMutassuk meg, hogy ha valamely (külső) pontból a kardioidhoz húzott
három érintő forgásszöge Θ1, Θ2, Θ3,
míg a pontot a kardioid
centrumával összekötő egyenes forgásszöge
φ, akkor Θ1 + Θ2 + Θ3 =
3φ, azaz
φ
az érintők forgásszögeinek átlaga.
szv00704 feladatMutassuk meg, hogy a kardioid bármely külső
pontjából (multiplicitással számolva) három érintő húzható a kardioidhoz.
Előzetes megjegyzés, segítség, megoldás és folytatási javaslat kérése
Házi feladatok
szv00705 feladatHány olyan kardioid van, amely egy adott háromszög
mindhárom oldalegyenesét érinti, és van olyan oldalegyenes, amelyet kétszer is?
Előzetes megjegyzés, segítség, megoldás és folytatási javaslat kérése