1. Geometriai feladatok
Ebbe a fejezetbe a geometria területéről válogattunk feladatokat.
Diákjaink számára a különböző
tárgykörök, pl. a geometria és a kombinatorika (vagy valószínűségszámítás)
összekapcsolása már önmagában is érdekes. Az alábbi területekről mutatunk
példákat:
- klasszikus valószínűség geometriai objektumok körében;
- klasszikus valószínűség meghatározása geometriai leírás segítségével;
- megoldás valamilyen geometriai megfeleltetés segítségével (geometriai valószínűségi mező);
- geometriai paradoxonok (5. fejezet).
A geometriai valószínűségi
mezőben az egyes események valószínűsége a hozzájuk rendelt geometriai
mértékkel arányos. Tehát a klasszikus valószínűség véges sok, egyformán
valószínű alapesetre felírható (kedvező esetek száma)/(összes eset száma)
meghatározási formuláját több szempontból is módosíthatjuk:
- végtelen sok eseményt is lekezelhetünk;
- az alapesetek nem szükségképpen egyformán valószínűek;
- a formula (megfelelő alakzat mértéke)/(teljes alakzat mértéke) alakra változik.
A geometriai valószínűséggel
megmutatható, hogy van olyan 0 valószínűségű esemény, ami bekövetkezhet. Ez a
diákok fantáziáját már önmagában is izgatja; motiváltságukat tovább
növelhetjük, ha a geometriai valószínűség segítségével eljutunk pl. a
feltételes valószínűség fogalmához. (A kombinatorika összeadási és szorzási
szabályát átvihetjük a valószínűségekre is.)
A cikk későbbi fejezeteiben is
találkozunk geometriai módszerek alkalmazásával.
Klasszikus
valószínűség geometriai objektumok körében
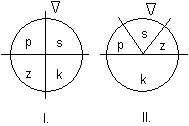
1.1. feladat:
Az I., ill.
II. pörgettyű körcikkeit kifestettük a piros, sárga, kék, zöld színekkel
(ábra). Ebben a játékban akkor nyerünk, ha előbb az I., majd a II. korongot
megpörgetve lila színt kapunk (kék + piros). Mennyi az esélyünk a nyerésre? (A
félkörnél kisebb körcikkek mindkét pörgettyűn egybevágók egymással.)
Első megoldás:
A
kombinatorika összeadási és szorzási szabályát alkalmazzuk.
Az első esetben I = piros és
II = kék színek valószínűsége 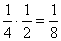 , a második esetben I =
kék és II = piros, ennek valószínűsége
, a második esetben I =
kék és II = piros, ennek valószínűsége 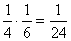 . Mivel vagy az
első, vagy a második eset következik be, a lila szín előállásának
valószínűsége
. Mivel vagy az
első, vagy a második eset következik be, a lila szín előállásának
valószínűsége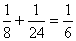 .
.
Második megoldás:
A
pörgetések lehetséges kimeneteleinek egy 4x6-os táblázat mezőit feleltethetjük
meg.
| II. pörgettyű: |
|
p |
s |
z |
k |
k |
k |
| I. pörgettyű: |
p |
|
|
|
|
|
|
| |
s |
|
|
|
|
|
|
| |
z |
|
|
|
|
|
|
| |
k |
|
|
|
|
|
|
Látható, hogy a 24 egység
területű táblázatból 6 egységnyi terület a megfelelő.
1.2. feladat (KöMaL F995.):
Mekkora
annak a valószínűsége, hogy az 1, 2, ..., 179 fokos szögekből tetszés szerint
választott 3 szög egy különböző oldalú háromszög három szöge?
Megoldás:
A szögeket
jelöljük x < y < z-vel, s végezzük el a következő becslést: x + y = 180°
– z, ezért x + y < 180° – y, s innen
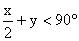
. Ezután határozzuk meg az
egyes x értékekhez tartozó lehetséges y értékeket:
ha x = 1°, y ∈ {2°, 3°, … , 89°}, 88 lehetőség;
ha x = 2°, y ∈ {3°, 4°, … , 88°}, 86 lehetőség;
ha x = 3°, y ∈ {4°, 3°, … , 88°}, 85 lehetőség;
ha x = 4°, y ∈ {5°, 4°, … , 87°}, 83 lehetőség;
…
ha x = 57°, y ∈ {58°, 59°, 60°, 61°}, 4 lehetőség;
ha x = 58°, y ∈ {59°, 60°}, 2 lehetőség;
ha x = 59°, y ∈ {60°}, 1 lehetőség.
Könnyen bizonyítható a
szabályosság: ha x a páratlan (vagy páros) számokon fut, a lehetőségek száma
hármasával csökken. A lehetőségek számai között a 3-mal oszthatóak fognak
hiányozni, a kedvező lehetőségek száma tehát (1 + 4 + 7 + … + 88) + (2 + 5 + 8
+ … + 86) = 2611. Az összes lehetőség 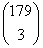 , a keresett valószínűség
, a keresett valószínűség 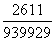 .
.
További feladatok:
1.3. feladat:
Mekkora
annak a valószínűsége, hogy az 1, 2, ..., 179 fokos szögekből tetszés szerint
választott három szög egy háromszög három szöge?
1.4. feladat:
Tetszőlegesen
kiválasztunk az [n + 1, 2n] zárt intervallumból három számot. Mi annak a
valószínűsége, hogy a három szám egy egyenlő szárú háromszög három oldalának
mérőszáma?
Geometriai támogatás
1.5. feladat:
Egy egér az
A jelű pontból elindul az ábrán jelölt járatokon lefelé, mert sajtszagot érez.
A sajtszag egyformán érezhető mindegyik csatornában, így az egér az
elágazásokban egyforma valószínűséggel választ az egyes járatok között (visszafelé
nem fordul). Sajt csak bizonyos járatok végén található az ábra szerint (S).
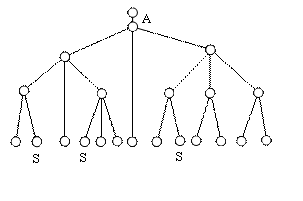
Mekkora annak a valószínűsége,
hogy az egér megtalálja a sajtot?
Megoldás:
Az összeadási
és szorzási szabályt alkalmazhatjuk. Így a három esetben rendre
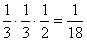
,
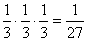
,
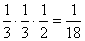
valószínűségeket
kapunk, a sajt megtalálásának valószínűsége ezek összege,
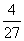
.
1.6. feladat:
Egy 4x4-es
négyzetrács alakú labirintus két átellenes csúcsában - a kijáratoknál - egy
egér és egy macska van. Mindketten adott jelre, ugyanakkora sebességgel
elindulnak a szemköztes kijárat felé úgy, hogy minden lépésben közelednek
céljukhoz (ábra). Egymást nem látják, útválasztásuk az elágazásokban
véletlenszerű. (Ez azt jelenti, hogy amikor elágazáshoz érnek, a lehetséges két
irány közül egyforma valószínűséggel választanak.)

Mekkora annak a valószínűsége,
hogy találkoznak?
Megoldás:
A találkozás a
négyzet átlója mentén történhet. Fentről lefelé haladva rendre 1, 4, 6, 4, 1 út
vezet mindkét oldalról a találkozási pontokba, így a kedvező esetek száma 1
2
+ 4
2 + 6
2 + 4
2 + 1
2 = 70. Mivel az
első négy lépést a macska is és az egér is tetszőlegesen választhatja ki két
irány közül, mindketten 2
4-féle utat tehetnek meg. Az összes eset
száma tehát 2
4·2
4
= 2
8, a keresett valószínűség
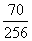
≈ 0,273.
Megjegyzés:
Könnyű
n x
n-es
táblázatra általánosítani, a formula
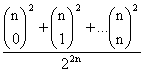
.
Sőt, az egér és a macska útját
együtt felfoghatjuk egy olyan (egyetlen) útnak, amely az egér és a macska
kezdeti helyét köti össze, ezért a kapott formula egyenlő 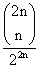 -nel is.
-nel is.
További feladatok:
1.7. feladat:
Az ábra
szerinti labirintusban a B bejáratból indulunk, fentről lefelé haladunk a
járatokban. Az elágazásokban az egyes járatok közül a rájuk írt
valószínűségekkel választunk (nem jelöltük a 0,5 valószínűségeket). Mekkora
annak a valószínűsége, hogy kijutunk valamelyik K kijáraton?
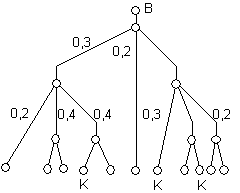
1.8. feladat:
Egy
Bolyongó Béka kezdetben a számegyenes 0 pontjában áll. A Béka minden lépésben
véletlenszerűen lép jobbra vagy balra egy egységnyit. Mekkora annak a
valószínűsége, hogy 10 lépés után
a) az 5 pontban lesz;
b) a 6 pontban lesz?
c) Melyik pontban lesz
legnagyobb valószínűséggel 10 lépés múlva?
1.9. feladat:
A Bolyongó
Béka most a számegyenes [– 5, 7] zárt intervallumán bolyong. (Ha a Béka az intervallum
valamelyik végpontján túlra ugrik, akkor véglegesen eltűnik a szemünk elől.)
a) Mekkora most annak a
valószínűsége, hogy 10 lépés után a 6 pontban lesz?
b) Mekkora annak a
valószínűsége, hogy elég sok lépés után jobbról hagyja el az intervallumot?
c) Átlagosan hány
lépésben hagyja el az intervallumot?
Megjegyzés:
A b) és c)
feladatok megoldásai legegyszerűbben a Markov-láncok segítségével végezhetők
el. A javasolt szakirodalmon kívül ebből a témából érdekes példák találhatók a
következő címen: (
link).
Geometriai
megfeleltetés (geometriai valószínűségi mező)
1.10. feladat:
4 mm-es átmérőjű
drótból készített kerítésen a szomszédos vízszintes és függőleges merevítő
drótok tengelyeinek távolsága 10 cm. (Ez egy nagyon ritka kerítés.) Mekkora
valószínűséggel ütközik valamelyik drótdarabnak egy véletlenszerűen kilőtt 4
mm-es sörétszem? (Feltehetjük, hogy a kerítés szabályos négyzetrács, és a sörét
a kerítés bármely pontjára ugyanakkora valószínűséggel érkezik.)
Megoldás:
Egybevágó
négyzetekkel fedhetjük le a rácsot, a négyzetek oldala a szomszédos drótok
tengelyeire esik (ábra).

A négyzet oldala 10 cm, ezeken
belülre nyúlik a kerítés drótjából 2 mm. Akkor nem fog a kerítésnek ütközni a
sörét, ha középpontja ettől a benyúlástól még legalább 2 mm-rel beljebb esik.
Tehát az esemény szempontjából a teljes alakzat 10 cm oldalú négyzet, a
komplementer esemény „kedvező” alakzata pedig egy 9,2 cm oldalú négyzet. Az
áthaladási valószínűség
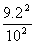 ≈ 0,8464, az ütközési valószínűség tehát ≈ 0,15.
≈ 0,8464, az ütközési valószínűség tehát ≈ 0,15.
Megjegyzés:
"A sörét a kerítés bármely pontjára ugyanakkora
valószínűséggel érkezik" - ez a valószínűség
természetesen 0 (bár nem lehetetlen esemény). Valójában azzal a
feltevéssel élünk, hogy annak valószínűsége, hogy a sörét a
kerítés valamely adott területére érkezik, arányos a terület
nagyságával. Ez persze csak egy modell,
melynek legfőbb előnye, hogy matematikailag könnyen kezelhető.
1.11. feladat:
a)
Egy sörétes patron 10 darabot tartalmaz a 4 mm-es átmérőjű sörétszemekből.
Mekkora valószínűséggel halad át mind a 10 sörétszem a kerítésen?
b) És ha a patron 20
szemet tartalmaz?
Megoldás:
a)
0,8464
10 ≈ 0,1887, vagyis az
ütközésmentes áthaladásra még 20% esély sincs.
b) 0,8464
20 ≈ 0,0356 a valószínűség, tehát rendkívül
kicsi.
Megjegyzés:
Kicsit
megvizsgálva 0,8464 hatványait, meglepő eredményekre jutunk. 0,8464
4
≈ 0,5132, tehát már 4 sörét esetén is
kb. ugyanakkora valószínűséggel történik a sima áthaladás, mint az ütközés;
nagyobb sörétszemekre pedig az érték rohamosan csökken. A jelenség neve a „kis
valószínűségek paradoxona”, erről valamivel részletesebben a 3.7. feladatban
olvashatunk.
1.12. feladat:
Egy pálcát
véletlenszerűen kettétörünk. Jelöljük a pálca végponjait A-val és B-vel, a
töréspontot Q-val.
a) Mekkora a
valószínűsége annak, hogy a Q pont közelebb lesz A-hoz, mint B-hez?
b) Mekkora a
valószínűsége annak, hogy a törés után az egyik szakasz legalább kétszer akkora
lesz, mint a másik?
Megoldás:
a) Az
eredmény nyilván
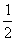
.
b) A három egyenlő részre
osztott pálca középső harmadába nem eshet a töréspont. A keresett valószínűség
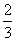
.
1.13. feladat:
Egy pálcát
véletlenszerűen három részre törünk. Jelöljük a pálca végponjait A-val és
B-vel, a töréspontokat Q-val és R-rel. Mekkora a valószínűsége annak, hogy a
törés után a három szakaszból háromszög szerkeszthető?
Megoldás:
Tekintsük
egységnyinek a pálca hosszát, s legyen AQ = x, AR = y. Feleltessük meg a két
töréspontot a sík egységnégyzete (x, y) pontjának; az (x, y) pont véletlenszerű
kiválasztása ekvivalens a két töréspont megjelölésével. Két esetet
különböztetünk meg:
I. eset: Ha x < y, akkor a
három szakasz hossza x, y – x, 1 – y. Ezekre kell a háromszög-egyenlőtlenségnek
teljesülnie, a kapott feltételek: x < 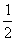 , y >
, y > 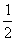 , y
< x +
, y
< x + 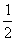 .
.
A ponthalmazoknak megfelelő
tartományt az ábrán I-gyel jelöltük.
II. eset: Ha y < x, akkor
szerepcserével y < 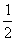 , x >
, x > 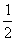 , x
< y +
, x
< y + 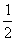 . A ponthalmazt II-vel
jelöltük.
. A ponthalmazt II-vel
jelöltük.
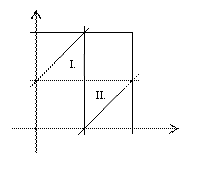
Az egyenlőtlenség-rendszernek
eleget tevő pontok halmaza az I. és II. tartomány, a keresett valószínűség 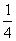 .
.
Megjegyzés:
A kimaradt x
= y eset annak felel meg, ha a Q és R töréspont egybeesik. Ennek az eseménynek
0 a valószínűsége (bár nem lehetetlen esemény).
1.14. feladat:
Két
személy megbeszéli, hogy de. 10 és 11 óra között találkoznak. Érkezésük ezen
időszak közben véletlenszerű. Mi annak a valószínűsége, hogy az előbb jövőnek
nem kell negyed óránál többet várnia?
Útmutatás:
Az előző
megoldás gondolatmenetét alkalmazhatjuk. Érkezzék az egyik személy x, a másik y
órával 10 óra után (x, y ≤ 1), s
az érkezésüket feleltessük meg ismét az egységnégyzet (x, y) koordinátájú
pontjának. Ekkor az
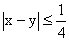
ponthalmaz területét kell
meghatároznunk.
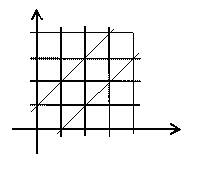
Eredmény:
A keresett
valószínűség
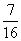
.
Következő fejezet
Tartalom



 .
.



