2. Van hiba az alábbi okoskodásokban?
A tanár szemszögéből nézve a
tanítás folyamatában érdekes témakör a kombinatorika. Eszközigénytelen, a
témával foglalkozó diáknak viszonylag kevés képletet kell ismernie. Ugyanakkor
a matematika semmilyen más területén nem olyan könnyű hibázni, mint itt: a
legegyszerűbb, ártatlan elemi feladat megoldása is meglepetést okozhat.
A kombinatorikában a hibás
feladatmegoldások módszertani szerepe igen nagy. Soha ne engedjük, hogy a
diákok megelégedjenek saját (szép) megoldásukkal; legalább ugyanolyan fontos,
hogy társaik esetleges hibás gondolatmenetét átlássák, megértsék, és
megtalálják benne a hibát.
Érdemes felhívni diákjaink
figyelmét arra, hogy a megismerési folyamat minden tudományágban a feltevések
folyamatos módosításán és a tévedések állandó javítgatásán, csiszolgatásán
alapul. Az elmúlt korok szellemi nagyjai számtalan tévút és zsákutca után érték
el eredményeiket, amiket most mi néhány letisztult tétel vagy alkalmazható elv
alakjában készen kapunk.
A megismerési folyamathoz
hasonlíthatjuk kicsiben a feladatmegoldás folyamatát is. Itt is szükség van
alkalmanként több nekifutásra, előfordulhatnak zsákutcák stb.
A valószínűségszámítás ma már
lényegesen túlnyúlt a kombinatorikán. Elmélete absztraktabb lett, a diákok
feladatmegoldásai között elég szép számmal találunk hibásakat, s a tanítás
folyamatában ezek részletes megvizsgálása rendkívül fontos. Hasonló cipőben
jártak őseink is. Nem is hinnénk, hogy a matematika történetével foglalkozó
kutatók a korábbi századok matematikusainak munkáiban hány olyan gondolatra
bukkannak, amely ma már egy pillanatra sem tudja lekötni a művelt középiskolás
diák figyelmét. Bár ebben a fejezetben lesz történeti érdekességekről szó, csak
egy példa: Jean le Rond d’Alembert XVIII. századi nagy francia matematikus nem
látta, hogy az eredmény ugyanaz, ha egy érmét dobunk fel háromszor, vagy ha
három érmét egyszerre.
A fenti módszertani indokok után
lássuk a feladatokat! A cikk többi részétől eltérően itt rögtön megadunk egy
megoldási gondolatmenetet (alkalmanként többet is), s a feladat egyrészt annak
eldöntése, hogy jó-e az okoskodás (ill. hogy melyik a jó), másrészt maga a hiba
feltárása. (Tehát nem elég egy másik, jó megoldást adni!)
Módszertani megfontolásokból,
galád módon, nem minden probléma esetén oldjuk fel az ellentmondásokat;
reméljük, hogy a kedves Olvasónak is kellemes fejtörést okozunk.
Természetesen nagyon egyszerű
feladatokkal kezdjük, ezek egy része már a legalapvetőbb általános műveltséghez
tartozik.
2.1. feladat:
Egy
dobozban 5 egyforma golyó van, néhány piros, néhány kék. Találomra kihúzunk egy
golyót. Mekkora annak a valószínűsége, hogy a kihúzott golyó piros?
Első gondolatmenet:
Nem
ismerjük a golyók színének eloszlását.
Vagy piros,
vagy kék
golyót húzunk ki; a piros golyó kihúzásának valószínűsége ezek szerint
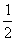
.
Második gondolatmenet:
A
golyók színeloszlásának ismerete nélkül csak a legvalószínűbb, tehát kb.
egyenletes eloszlást tételezhetjük fel. Mivel 2,5 golyó nincs, két esetet
vizsgálunk.
Ha 3 piros golyó van (ezt az
esetet 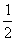 valószínűségűnek
tekintjük), akkor piros golyót
valószínűségűnek
tekintjük), akkor piros golyót 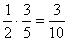 valószínűséggel húzunk;
ha pedig 3 kék golyó van, akkor pirosat
valószínűséggel húzunk;
ha pedig 3 kék golyó van, akkor pirosat 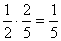 valószínűséggel húzunk. A
két eset valamelyike
valószínűséggel húzunk. A
két eset valamelyike 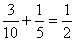 valószínűséggel
következik be.
valószínűséggel
következik be.
Megjegyzések:
1. Ez a feladat a
puristák és a laxisták (modernisták) „küzdelmének” alapfeladata lehetne. (A
puristák a valószínűségszámítás érvényességét arra próbálják meg korlátozni,
amire azt kitalálták; a laxisták pedig próbálják minél több dologra
kiterjeszteni, pl.: az időjárásra, Földön kívüli értelem létezésére stb.) A
harc - a puristák tisztán matematikai megfontolásai ellenére - váltakozó
sikerrel (alkalmanként kompromisszumokkal) folyik. Erről további gondolatok pl.
a [7] szakirodalomban olvashatók.
2. Azt javasoljuk, hogy
az ilyen típusú problémákat azért a puristák módszerével kezeljük le; mely
szerint ebben a feladatban a valószínűségszámítás módszerei egyáltalán nem
alkalmazhatók.
2.2. feladat:
Két
dobókockával dobunk, a dobott számok összegét tekintjük. Melyik esemény
valószínűbb?
A esemény: a dobott számok
összege legalább 10;
B esemény: a dobott számok
összege legfeljebb 4.
Gondolatmenet:
Nagyobb
számokat nehezebb dobni a tapasztalat alapján, a B esemény a valószínűbb.
Megjegyzések:
1. Matematikai
szemléletünk a szimmetriaokok miatt nyilván az egyforma valószínűséget
sugallja, s a számolás is ezt igazolja.
2. Az olyan típusú
társasjátékokban, ahol előnyös nagyot dobni a kockával, gyakran érezzük úgy,
hogy többször dobunk kis számot, s ritkábban nagyot. Mi lehet ennek az oka?
A jelenség valószínűleg
pszichológiai eredetű. A sikeres dobást boldogan tudomásul vesszük, a kudarcra
(egy hosszú pechsorozatra) viszont sokáig emlékezünk.
3. Egyes esetekben
viszont Murphy törvényének (a másik sor mindig rövidebb, a másik irányból
mindig hamarabb jön a busz stb.) gyakorlati okai lehetnek, lásd pl. a 3.1. vagy
3.2. feladatokat és a hozzá fűzött megjegyzéseket.
2.3. feladat:
Egy
pénzdarabot feldobtunk egymás után 9-szer, mindegyik dobás eredménye írás volt.
Melyik a valószínűbb esemény?
A: a 10. dobás is írás lesz;
B: a 10. dobás fej lesz.
Első gondolatmenet:
Ilyen
sok írás után sokkal valószínűbb egy fej dobás. (Így okoskodott pl. a
bevezetőben említett XVIII. századi francia matematikus, d’Alembert is.)
Második gondolatmenet:
Annak
valószínűsége, hogy 10 írásból álló sorozat jön ki,
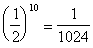
, rendkívül kicsi.
Sokkal valószínűbb tehát egy fej dobás.
Megjegyzések:
1. Ma már tudjuk, hogy a
10. dobás nem függ az első 9 dobástól, a fenti okoskodások hibásak.
2. A középiskolás
gyerekek megmosolyogják a fenti gondolatmeneteket. Hívjuk fel a figyelmüket a
bevezetőben említett gondolatokra, s kérjük meg, hogy képzeljék őseink helyébe
magukat. Kérdezzük meg, hogy ha pl. most ruletteznének, s egymás után 9-szer
jött már ki a piros, vajon melyik színre tennének?
2.4. feladat:
Két
teljesen egyforma, külsőre megkülönböztethetetlen kockát feldobunk, a dobott
számok összegét tekintjük. Mekkora annak a valószínűsége, hogy a dobott számok
összege 7?
Első gondolatmenet:
Mivel
a kockák teljesen egyformák, 11-féle lehetséges összeg van: 2, 3, ... , 12.
Ebből egy eset kedvező, a keresett valószínűség
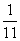
.
Második gondolatmenet
(Gottfried
Wilhelm Leibniz (1646 - 1716) német matematikus és filozófus)
: Az egyes
összegek többféleképpen is előállhatnak (táblázat).
|
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
|
1+1
|
1+2
|
1+3
2+2
|
1+4
2+3
|
1+5
2+4
3+3
|
1+6
2+5
3+4
|
2+6
3+5
4+4
|
3+6
4+5
|
4+6
5+5
|
5+6
|
6+6
|
|
db:
|
1
|
1
|
2
|
2
|
3
|
3
|
3
|
2
|
2
|
1
|
1
|
A 21 lehetséges összegből 3
állítja elő a 7-et, így a keresett valószínűség
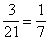 .
.
Harmadik gondolatmenet:
Hiába egyforma külsőre a két kocka, azért csak különböznek egymástól. Így az
előző táblázat módosul:
|
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
|
1+1
|
1+2
2+1
|
1+3
2+2
3+1
|
1+4
2+3
3+2
4+1
|
1+5
2+4
3+3
4+2
5+1
|
1+6
2+5
3+4
4+3
5+2
6+1
|
2+6
3+5
4+4
5+3
6+2
|
3+6
4+5
5+4
6+3
|
4+6
5+5
6+4
|
5+6
6+5
|
6+6
|
|
db:
|
1
|
2
|
3
|
4
|
5
|
6
|
5
|
4
|
3
|
2
|
1
|
A keresett valószínűség 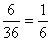 .
.
Megjegyzések:
1. Komoly probléma, hogy
a valószínűségszámításban bizony mást jelent a különbözőség és mást a
megkülönböztethetőség fogalma. Külsőleg hiába teljesen egyforma két kocka,
azért különböznek egymástól (pl. befesthetők). Az első gondolatmenet nem jó.
2. Leibniz még azt hitte,
hogy két kockával pontosan olyan könnyű 12-t dobni, mint 11-et. Az utolsó két
oszlop mutatja tévedését.
3. Tanítás közben (kb. 7.
osztály környékén) a gyakorlat alapján kell meggyőznünk a diákokat; pl.
dobassunk minden gyerekkel otthon 100 dobást, összegezzünk, s határozzuk meg a
relatív gyakoriságot: 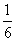 -hoz vagy
-hoz vagy
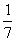 -hez van közelebb?
-hez van közelebb?
2.5. feladat:
Egy fiút
akkor engednek el játszani, ha három egymás utáni sakkparti közül legalább két
egymás utánit megnyer. Partnerei: Apa és Papa, mégpedig vagy Apa-Papa-Apa, vagy
Papa-Apa-Papa sorrendben. Apa jobban játszik, mint Papa. Melyik sorrend
kedvezőbb a fiú számára?
Gondolatmenet:
Nyilván a
gyengébben játszó Papával érdemes több mérkőzést játszani, kedvezőbb a Papa-Apa-Papa
sorrend.
Megjegyzések:
1. Hát nem. Legyen a fiú
nyerésének valószínűsége Apa ellen a, Papa ellen p (p > a), s számoljuk ki
mindkét esetben a fiú számára sikeres mérkőzéssorozat valószínűségét.
Az Apa-Papa-Apa mérkőzések
esetén vagy az első két mérkőzést kell megnyernie (ennek valószínűsége ap),
vagy az utolsó kettőt (pa). Kétszer számoltuk azt az esetet, amikor mind a
három mérkőzést megnyeri, így a keresett valószínűség 2ap – a2p.
Hasonlóan számolva a Papa-Apa-Papa
sorozatot, a valószínűség 2ap – p2a.
Összehasonlítva a két értéket,
kedvezőbb az Apa-Papa-Apa sorozat.
2. Ennek az egyszerű
paradoxonnak (érdekességnek) az az oka, hogy a fiúnak a középső mérkőzést
mindenféleképpen meg kell nyernie, s végső soron kedvezőbb számára, ha ezt a
gyengébb Papával játssza.
2.6. feladat:
Egy érmét
kétszer feldobunk. Mekkora annak a valószínűsége, hogy legalább egy esetben fej
lesz felül?
Első gondolatmenet
(D'Alembert,
1754)
: Három eset lehetséges. Vagy az első alkalommal dobunk fejet, vagy
a második alkalommal, vagy egyik esetben sem. E három eset közül kettő kedvező,
a keresett valószínűség
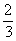
.
Második gondolatmenet:
Három eset lehetséges. Vagy két írást dobunk, vagy két fejet, vagy egy fejet és
egy írást. A keresett valószínűség
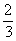
.
Megjegyzések:
1. Lényegében mindkét
gondolatmenetnek ugyanaz a hibája, hogy ti. az alapesetek nem egyformán
valószínűek. Az első esetben nem kizáró eseményekkel dolgozik a megoldó, a
második esetben pedig ismét fellép a 2.4. feladat megkülönböztethetőségi
problémája.
2. A helyes megoldáshoz
többféleképpen eljuthatunk.
Módosíthatjuk az első
gondolatmenetet (fejet dobunk az első alkalommal; vagy másodszor, ha először
írást dobtunk); vagy kiszitálhatjuk a duplán számolt fej - fej dobásokat.
A második gondolatmenet
módosítása csak annyiból áll, hogy a fej - írás és írás - fej sorozatokat
megkülönböztetjük.
Végül eljárhatunk egészen
másképpen is, pl. a komplementer eseményt határozzuk meg.
2.7. feladat
(osztozkodás-paradoxon):
Két játékos egy szabályos érmével játszik. András
akkor győz, ha - nem szükségképpen egymás után - öt fej jön ki, Béla pedig
akkor, ha öt írás. A játszma négy fej, két írás állásnál véglegesen
félbeszakad. Hogyan osztozzanak a játékosok az 1600 Ft-os téten?
Első gondolatmenet:
Az
összeget 4 : 2 arányban kell felosztaniuk, hiszen ennyi a dobott fejek és
írások aránya.
Második gondolatmenet:
Az
összeget 3 : 1 arányban kell felosztaniuk, hiszen ennyi fej, illetve írás dobás
hiányzik a játékosok győzelméhez.
Harmadik gondolatmenet:
Még
nincs vége a játéknak,
vagy András nyer,
vagy Béla. Az arány
legyen 1 : 1, így igazságos.
Negyedik gondolatmenet
(Niccolo
Tartaglia (1499 - 1557) olasz matematikus)
: Andás 2 játékkal nyert
többet, mint Béla, ezért meg kell kapnia az összes tét
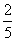
részét, a
maradékot pedig fele-fele arányban kell elosztani. Az arány 7 : 3.
Ötödik gondolatmenet:
A 4
fej, 2 írás valószínűsége
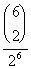
=
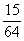
. Ennyivel volt
szerencsésebb András, ezért a javasolt osztozkodási arány 49 : 15.
Hatodik gondolatmenet:
Csak
az egyenlőnek számító "2 fej - 2 írás" álláshoz képest történt
változást vizsgáljuk. András előnyösebb helyzetben van 2 fej dobással. A 2
többletdobás kimenetele 4-féle lehet, a 2 fej dobás
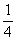
valószínűségű.
Ennek megfelelően a helyes osztozkodási arány 3 : 1.
Megjegyzések:
1. A fenti megoldások
mindegyikét diákjaim javasolták, de egyik sem jó.
A feladat megoldásakor az a
helyes kiindulási alap, ha azt vizsgáljuk meg, hogy a játékot tovább folytatva,
a játék befejezéséig mekkora valószínűséggel nyerne
András, illetve Béla. A hasonló típusú bonyolultabb feladatok a Markov-láncok
segítségével elegánsan tárgyalhatók (link),
most erre nincs szükségünk.
Ugyanis Béla csak akkor
nyerhetne, ha a következő három dobás mindegyike írás lenne, ennek
valószínűsége pedig 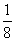 . Minden
más esetben András nyer, a helyes osztozkodási arány 7 : 1.
. Minden
más esetben András nyer, a helyes osztozkodási arány 7 : 1.
2. Egy kis
matematikatörténet: Már 1380-as és 1494-es kéziratokban is találkozunk a
paradoxonnal, de a korabeli megoldók még azt sem vették észre, hogy a feladat
egyáltalán valószínűségszámítási jellegű. 1654-ben Pascal és Fermat egymástól
függetlenül megoldotta a problémát, s ez akkoriban olyan komoly felfedezésnek
számított, hogy sokan ma is ettől az időponttól számítják a valószínűségszámítás
megszületését. Végül 1657-ben Huygens három játékos esetére is általánosította
a problémát.
További feladatok
Az alábbiakban kitűzött feladatok
megoldásai között szép számmal lesznek hibásak is. Döntsük el, hogy mi a hiba
az egyes gondolatmenetekben! (Vigyázat: abból, hogy két eredmény ugyanaz, még
nem következik, hogy mindkét gondolatmenet jó is!)
Az eredmények a fejezet végén, a
függelékben olvashatók.
2.8. feladat:
Egyszerre
dobunk fel három érmét. Mi annak a valószínűsége, hogy mindegyiknek ugyanaz az
oldala kerül felülre?
Gondolatmenet:
Az érmék
között biztosan lesz két egyforma. Annak valószínűsége, hogy a harmadik
ugyanilyen lesz,
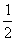
.
2.9. feladat:
Andrásnak
két golyója van, Bélának egy. A golyók elgurítása után megnézik, melyiküké
közelített meg jobban egy kitűzött pálcát (a pálca és a golyók távolságai mind
különbözők). Ha mind a két játékos ugyanolyan ügyes, akkor mi annak a
valószínűsége, hogy András győz?
Első gondolatmenet:
Béla
második dobása nem függ András két dobásától. Ha a két játékos egyformán ügyes,
véletlenszerű lesz a golyók és a pálca távolsága (ugyanolyan eséllyel dob
közelebbit, mint távolabbit Béla). A keresett valószínűség P =
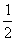
.
Második gondolatmenet:
Három eset van, a golyók sorrendje lehet AAB, ABA, BAA. Ebből 2 eset kedvező
András számára, P =
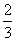
.
Harmadik gondolatmenet:
Három eset lehetséges. A célhoz legközelebb lehet András első, András második,
vagy Béla egyetlen golyója, ezért P =
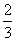
.
Negyedik gondolatmenet:
A
harmadik gondolatmenet „gyanús”. Ugyanis annak valószínűsége, hogy András
valamelyik golyója megelőzi Béla valamelyik golyóját,
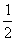
; tehát annak
valószínűsége, hogy két golyója is közelebb lesz a pálcához,
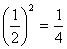
, s ez
mutatja, hogy a harmadik gondolatmenetben nem egyformán valószínűek az egyes
esetek. Alkalmazzuk a komplementer megoldás módszerét! Annak valószínűsége,
hogy Béla golyója megelőzi András mindkét golyóját,
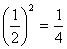
, ezért P =
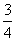
.
Ötödik gondolatmenet:
Különböztessük meg András két golyóját! Ekkor négy eset lehetséges: vagy András
mindkét golyója közelebb van, mint Béla golyója; vagy András mindkét golyója
távolabb van; vagy András első golyója közelebb van, a második távolabb; vagy
fordítva. P =
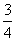
.
2.10. feladat:
András és
Béla a következő kockajátékot játsszák. András dobókockáján a 2, 2, 2, 5, 5, 5;
Béla kockáján a 3, 3, 3, 3, 3, 6 számok vannak. Mindkét játékos feldobja saját
kockáját, s az nyer, aki nagyobbat dobott. Kinek előnyös a játék?
Gondolatmenet:
Mindkét
kockán ugyanannyi a számok összege, vagyis ugyanannyi a számok átlaga. A játék
igazságos.
2.11. feladat:
Módosítjuk
az előző játékot, Béla kockáján kicseréljük az egyik 3-ast 1-esre: 1, 3, 3, 3,
3, 6. Ez a játék most már Andrásnak előnyös?
Megjegyzés:
Látható, hogy
az előző gondolatmenet „gyanús”. A feladattal kapcsolatos problémákat
részletesen megvizsgáljuk az
ötödik fejezetben.
2.12. feladat:
Egy
dobozban 3 piros, 1 fehér és 1 kék, egyforma méretű golyó található. A golyókat
véletlenszerűen kihúzzuk egymás után és egy sorozatot készítünk belőlük. Melyik
sorrend a valószínűbb: a pppfk (tehát amikor a három pirosat húzzuk ki először)
vagy a kfppp?
Gondolatmenet:
Nyilván
első közelítésben annyit mondhatunk, hogy a sorozat első két helyén inkább
piros golyók lesznek.
Függelék
A 2.8. - 2.12. feladatok
eredményei:
2.8. A valószínűség 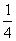 .
.
2.9. Egyik gondolatmenet
sem jó. P = 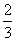 . (Indoklásul elég annyit
mondanunk, hogy 6 alapeset van: 12B, 21B, 1B2, 2B1, B12, B21.)
. (Indoklásul elég annyit
mondanunk, hogy 6 alapeset van: 12B, 21B, 1B2, 2B1, B12, B21.)
2.10. A játék Bélának
előnyös.
2.11. A játék igazságos.
2.12. A sorozatok
egyformán valószínűek.
Előző fejezet
Következő fejezet
Tartalom
![]() valószínűségűnek
tekintjük), akkor piros golyót
valószínűségűnek
tekintjük), akkor piros golyót ![]() valószínűséggel húzunk;
ha pedig 3 kék golyó van, akkor pirosat
valószínűséggel húzunk;
ha pedig 3 kék golyó van, akkor pirosat ![]() valószínűséggel húzunk. A
két eset valamelyike
valószínűséggel húzunk. A
két eset valamelyike ![]() valószínűséggel
következik be.
valószínűséggel
következik be.