1. találat: ARANYD 2013/2014 Haladó I. kategória 1. forduló 1. feladat
Témakör: *Számelmélet (Azonosító: AD_20132014_h1k1f1f )
Ha $ A = 1 111 111 111 $ és $ B = 111 111 $, akkor mennyi $ A $ és $ B $ legnagyobb közös osztója?
*Algebra (Azonosító: AD_20132014_h1k1f2f )
Mennyi az $f(x)=|x^2-x|+|x^2+3x+2|$ függvény legnagyobb és legkisebb értéke a $\left[-\dfrac{3}{2};\dfrac{1}{2}\right]$ zárt intervallumon? Mely helyeken veszi fel ezeket az értékeket?
*Geometria (Azonosító: AD_20132014_h1k1f3f )
Mekkora a színezett részek területeinek összege, ha a kis körök sugara r?
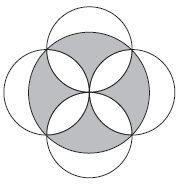
*Algebra (Azonosító: AD_20132014_h1k1f4f )
Legyen $A=\dfrac{1}{2-\sqrt{3}}$, $B=\left(\sqrt{5}-\sqrt{2\sqrt{3}}\right)\left(\sqrt{2\sqrt{3}}+\sqrt{5}\right)$, $C=\sqrt{7-4\sqrt{3}}$. Bizonyítsuk be, hogy a $K=\sqrt{(A+B-C)\cdot n +2}$ kifejezés értéke minden n természetes szám esetén irracionális!
*Algebra (Azonosító: AD_20132014_h1k1f5f )
Egy kocka csúcsait megcímkézzük az $ 1;\ 2;\ \ldots\ ;\ 8$ számokkal (minden címkét pontosan egy csúcsra írunk fel). A kocka egy lapjának értéke: a lapot határoló csúcsokon lévő számok összege. Legfeljebb mekkora lehet egy kocka legkisebb értékű lapjának értéke?
*Algebra (Azonosító: AD_20132014_h1k2f1f )
Legyen $f(x)=ax+b$ egy elsőfokú polinom. Bizonyítsuk be, hogy nem lehet az
$|f(0)-1|,\quad |f(1)-3|,\quad |f(2)-9|$
számok mindegyike 1-nél kisebb.
*Algebra (Azonosító: AD_20132014_h1k2f2f )
Határozzuk meg azokat a négyjegyű számokat, ahol az első két számjegyből álló szám és az utolsó két számjegyből álló szám összegének négyzete egyenlő az eredeti számmal!
*Geometria (Azonosító: AD_20132014_h1k2f3f )
Az O középpontú körvonal két pontja A és B, továbbá $AOB\angle=60^\circ$. A rövidebb AB ív tetszőleges belső pontja M. Bizonyítsuk be, hogy az OBMA négyszög középvonalai egymásra merőlegesek. (A négyszög középvonalainak a szemközti oldalak felezőpontját összekötő szakaszokat nevezzük.)
*Kombinatorika (Azonosító: AD_20132014_h1k2f4f )
Soma az ötödik születésnapi bulijára 5 barátját hívhatta meg. El is készült az 5 névre szóló meghívó, és készült hozzá 5 felcímzett boríték is. Soma azonban még nem tud olvasni, és úgy rakta be a borítékokba a meghívókat, hogy végül senki sem a sajátját kapta kézhez. Hányféleképpen lehet így elrendezni a meghívókat?
*Kombinatorika (Azonosító: AD_20132014_h1kdf1f )
Az S8Q-bolygón n különböző ország osztozik (50 < n < 80). Bármely két különböző ország között vagy baráti, vagy ellenséges a kapcsolat (harmadik eset nincs, és a kapcsolat kölcsönös) a következ˝o két szabály mellett:
Ha A, B, C három különböző ország, és
(1) A barátságos B-vel, valamint B barátságos C-vel, akkor A is barátságos C-vel. (barátom barátja a barátom)
(2) A ellenséges B-vel, és B is ellenséges C-vel, akkor A barátságos C-vel. (ellenségem ellensége a barátom )
Valamint tudjuk, hogy az n ország között lévő összes lehetséges viszonynak éppen a fele baráti, a másik fele ellenséges. Hány ország van az S8Q-bolygón?
*Geometria (Azonosító: AD_20132014_h1kdf2f )
Egy háromszög oldalainak mérőszámai egész számok. A háromszögbe írt kör r, és a hozzáírt körök r1, r2, r3 sugarainak mérőszámai páros egész számok. Tudjuk még, hogy,
$r \cdot r_1 \cdot r_2 + r \cdot r_2 \cdot r_3 + r \cdot r_3 \cdot r_1 + r_1 \cdot r_2 \cdot r_3 = r \cdot r_1 \cdot r_2 \cdot r_3 $
Bizonyítsuk be, hogy a háromszög derékszögű!
*Számelmélet (Azonosító: AD_20132014_h1kdf3f )
Egy n pozitív egész szám 17-edíziglen izgalmas, ha a következő feltételek teljesülnek rá:
(1) nincs (az 1-en kívül) négyzetszám osztója;
(2) pontosan 16 pozitív osztója van;
(3) ha nagyság szerint sorba rendezem a 16 darab pozitív osztót, akkor a 10-dik, és a 7-dik osztó különbsége éppen 17.
Kérdés: Hány 17-edíziglen izgalmas szám van?
*Számelmélet (Azonosító: AD_20132014_h2k1f1f )
Melyik az a legkisebb 28-cal osztható pozitív szám, amelynek a 10-es számrendszerbeli alakja 28-ra végződik, és számjegyeinek összege 28?
*Algebra (Azonosító: AD_20132014_h2k1f2f )
Oldjuk meg a valós számok halmazán az alábbi egyenletet:
$(x-5)(x-6)(x-7)(x-8)=120$
*Geometria (Azonosító: AD_20132014_h2k1f3f )
Az ABC háromszög AB oldalának A-n túli meghosszabbításán felvettük a P pontot, a BC oldal B-n túli meghosszabbításán az R pontot, végül az AC oldal A-n túli meghosszabbításán a Q pontot úgy, hogy AP = AB, CB = BR és CA = AQ. Mennyi a PQR háromszög területe, ha az ABC háromszögé $ 100\ cm^2$?
*Számelmélet (Azonosító: AD_20132014_h2k1f4f )
Osztható-e 81-gyel a 81 darab egyesből álló szám?
*Kombinatorika (Azonosító: AD_20132014_h2k1f5f )
Egy 2013x2013 méretű táblázat minden mezőjébe az 1-től 2013-ig terjedő egész számok valamelyikét írtuk be úgy, hogy semelyik sorba nem kerültek egyenlő számok, és a táblázat szimmetrikus lett az egyik átlójára. Bizonyítsuk be, hogy ekkor ebben az átlóban sem fordulnak elő egyenlő számok.
*Algebra (Azonosító: AD_20132014_h2k2f1f )
Legyen $f(x)=ax+b$ egy elsőfokú polinom. Bizonyítsuk be, hogy nem lehet az
$|f(0)-1|,\quad |f(1)-3|,\quad |f(2)-9|$
számok mindegyike 1-nél kisebb.
*Geometria (Azonosító: AD_20132014_h2k2f2f )
Mutassuk meg, hogy egy tetszőleges háromszögben $a^2+4m_a^2\le (b+c)^2$, ahol a, b és c a háromszög oldalainak hosszát, ma az a oldalhoz tartozó magasságot jelenti!
*Algebra (Azonosító: AD_20132014_h2k2f3f )
Oldjuk meg az egész számok halmazán a $ 2x^2y^2+y^2=6x^2+12$ egyenletet!
*Kombinatorika (Azonosító: AD_20132014_h2k2f4f )
Legyen $H = \{1; 2; 3; 4; 5; 6; 7; 8; 9\}$. H egy nemüres részhalmazát átlagosnak hívjuk, ha a benne szereplő számok átlaga megegyezik 5-tel (pl. az L = {3; 4; 8} ilyen). Hány átlagos részhalmaza van H-nak?
*Geometria (Azonosító: AD_20132014_h2kdf1f )
Adjunk meg a síkban 7 pontot úgy, hogy közülük bármely 4 között mindig legyen 3 olyan, hogy azok, mint csúcsok derékszögű háromszöget határozzanak meg.
*Számelmélet (Azonosító: AD_20132014_h2kdf2f )
Legyen n pozitív egész. Mutassuk meg, hogy az $A_n = 2^{2^n} + 2^{2^{n-1}} + 1$ számnak legalább n különböző prímosztója van.
*Algebra (Azonosító: AD_20132014_h2kdf3f )
Mennyi az $f(x) = x^{2014} +2x^{2013} +3x^{2012} +. . .+2013x^{2} +2014x+2015$ függvény legkisebb értéke?
*Algebra (Azonosító: AD_20132014_h3k1f1f )
Legyenek a, b, c és d olyan valós számok, amelyekre $ab = 1$ és $ac+bd = 2$. Bizonyítsuk be, hogy $cd \le 1$.
*Kombinatorika (Azonosító: AD_20132014_h3k1f2f )
Egy bizottság 40-szer ülésezett. Mindegyik ülésen 10 fő volt jelen. A bizottság bármelyik 2 tagja legfeljebb egy ülésen volt együtt. Bizonyítsuk be, hogy a bizottság legalább 64 tagból áll!
*Algebra (Azonosító: AD_20132014_h3k1f3f )
Melyek azok a p pozitív prímszámok, amelyekre a
$p+1=2x^2$
$p^2+1=2y^2$
egyenletrendszernek van egész megoldása?
*Geometria (Azonosító: AD_20132014_h3k1f4f )
Legyen a P pont az ABC egyenlő szárú derékszögű háromszög AB átfogójának tetszőleges pontja. A P pont merőleges vetülete AC-n az R, BC-n a Q pont. Bizonyítsuk be, hogy
a) Az RQ szakaszok felezőmerőlegesei egy ponton mennek át;
b) P-ből az RQ szakaszra bocsátott merőlegesek is egy ponton mennek át!
*Kombinatorika (Azonosító: AD_20132014_h3k1f5f )
Egy nxn-es tábla egyik mezőjén áll egy bábu. Egy lépésben mozoghatunk egyet fel, vagy egyet jobbra, vagy átlósan balra lefele egyet. Lehetséges-e, hogy a táblát úgy járjuk be, hogy minden mezőt pontosan egyszer érintünk, és végül a kiindulási mezőtől eggyel jobbra érkezünk meg?
*Algebra (Azonosító: AD_20132014_h3kdf1f )
Az x, y, z pozitív egész számokról tudjuk, hogy relatív prímek, és $\dfrac 1 x + \dfrac 1 y = \dfrac 1 z$. Bizonyítsuk be, hogy ekkor $x\cdot y\cdot z$ négyzetszám!


