Melyek azok az (a; b) egész számpárok, amelyekre teljesül az alábbi egyenlőtlenség:

$a^2+7b^2\le4ab+6b?$

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

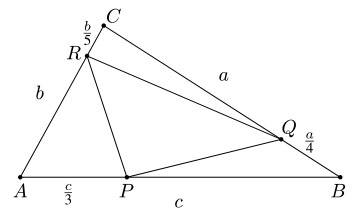
Adott az ABC háromszög. Legyen P az AB oldal harmadoló pontja, Q a BC oldal negyedelő pontja, valamint R a CA oldal ötödölő pontja az ábrán látható módon. Határozzuk meg a P QR és az ABC háromszögek területének arányát.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Oldjuk meg a következő egyenletet a valós számok halmazán:

$\sqrt{x+\sqrt{x}}-\sqrt{x-\sqrt{x}}=\dfrac{3}{2}\sqrt{\dfrac{x}{x+\sqrt{x}}}$

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

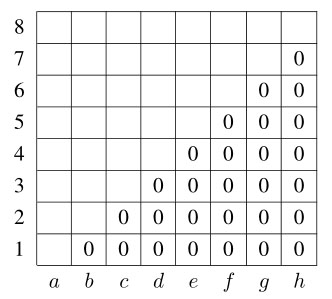
Adott egy 8 × 8-as táblázat. Nevezzük főátlónak az a₁ – h₈ átlót. A főátló alatti mezőket 0-kal töltjük ki, míg a többi mezőbe pozitív egészeket írunk. A kitöltés után kiszámoljuk a sor-, illetve oszlopösszegeket. Lehetséges-e, hogy az 1, 2, 3, . . . , 16 számokat kapjuk eredményül (valamilyen sorrendben)?

b) Ha egy 7 × 7-es táblánk van, akkor lehetséges-e, hogy az 1, 2, 3, . . . , 14 számokat kapjuk eredményül (valamilyen sorrendben)?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba