A k valós paraméter értékétől függően hány valós megoldása van a következő egyenletnek?
$\left| \left| \left| \left|x\right|-1\right|-2\right|-3\right|=x-k$
Határozzuk meg az összes olyan négyjegyű négyzetszámot, amelynek számjegyeit eggyel megnövelve a kapott négyjegyű szám szintén négyzetszám lesz!
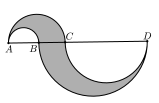
Az AB, AC, BD és CD szakaszok, mint átmérők felé félköríveket rajzoltunk az ábrán látható módon. Fejezzük ki a színezett rész területét a és b segítségével, ha AD = a és BC = b!
El lehet-e helyezni egy asztalon egy síkban (a pénzérmék egymásra helyezése nélkül)
a) 2016
b) 2017
egyforma, kör alakú pénzérmét úgy, hogy mindegyik pénzérme három másik pénzérmét érintsen? Ha el lehet helyezni, akkor egy lehetséges elhelyezést kérünk indoklással; ha nem lehet, akkor indoklást, hogy miért nem!
Tekintsük a következő 99 darab egyenletből álló 99 változós egyenletrendszert!
$\begin{cases}a_1+a_2=1\\a_2+a_3=2\\a_3+a_4=3\\\ldots\\a_{98}+a_{99}=98\\a_{99}+a_1=99\end{cases}$
Mennyi a következ˝o összeg pontos értéke?
$S=a_1-a_2+a_3-a_4\pm\ldots+a_{97}-a_{98}+a_{99}$


