Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
Látogatók
Összes:
9 200 851
Mai:
452
216.73.216.41
(IP: 216.73.216.41)
|
1. találat: ARANYD 2016/2017 Haladó III. kategória döntő 1. feladat
Témakör: *Geometria (háromszög, hasonlóság) (Azonosító: AD_20162017_h3kdf1f )
Az ABC háromszög hegyesszögű. Minden magasságszakaszán felvesszük a csúcstól távolabbi harmadolópontokat, legyenek ezek rendre A′, B′, C ′. Igazoljuk, hogy az ABC és az A′B′C ′ háromszögek hasonlóak.
*Kombinatorika (Azonosító: AD_20162017_h3kdf2f )
A H halmazt hívjuk izgalmas halmaznak, ha olyan véges, valós számokból álló halmaz, hogy minden $x\in H$ esetén $x^2-x\in H$ is teljesül. Hány elemű az a G halmaz, amely az összes lehetséges 2017-elemű izgalmas H halmazok uniója?
*Kombinatorika (Azonosító: AD_20162017_h3kdf3f )
Adott egy 8 × 8-as sakktábla. Nevezzük főátlónak az a1–h8 átlót. Az átló alatti mezőket 0-kal töltjük ki, míg a többi mezőbe pozitív négyzetszámokat írunk. A kitöltés után megvizsgáljuk a sor-, illetve oszlopösszegeket. Legkevesebb hány különböző szám lehet a 16 összeg között? 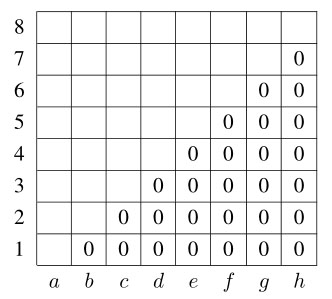
|
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
|
QR kód
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium

|
|
Bejelentkezés cikkíróknak
|
|


