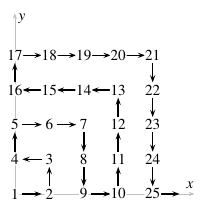1. találat: ARANYD 2017/2018 Kezdő I. kategória és II. kategória 2. forduló, III. kategória 1. forduló 1. feladat
Témakör: *Geometria (szög) (Azonosító: AD_20172018_k1k2f1f, AD_20172018_k2k2f1f, AD_20172018_k3k1f1f )
Az ABCD szimmetrikus trapézban $AB || CD$ és $AB \ge CD$. E és F a BC, illetve CD oldalak egy-egy belső pontja. Tudjuk, hogy CE=CF. Az EF egyenes az AD egyenest a G pontban metszi. Mekkorák a trapéz szögei, ha a DFG háromszög egyenlő szárú?
*Algebra (Azonosító: AD_20172018_k1k2f2f, AD_20172018_k2k2f2f, AD_20172018_k3k1f2f )
Mutassuk meg, hogy tetszőleges a , b , c valós számok esetén a következő számok között biztosan van legalább egy olyan, amelyik nem negatív: $ 4a^2 - 2b + 1,\ b^2 + 2c + 4$, és $c^2-8a+ 1$
*Algebra (Azonosító: AD_20172018_k1k2f3f, AD_20172018_k2k2f3f, AD_20172018_k3k1f3f )
Egy iskola igazgatója összehívta az osztályok küldöttjeit (összesen 32 tanulót), hogy választ kapjon az alábbi kérdésekre:
a) Kezdődjön-e fél órával később a tanítás?
b) Jó lenne-e, ha a testnevelés órák a tízórai szünet előtt lennének megtartva?
c) Szeretnék-e a tanulók, ha a rajzórák szerdánként lennének?
A szavazásról a következőket tudjuk. A korai testnevelés órákat csak 16-an támogatták, az első kérdésre 17, míg a harmadikra 25 igen szavazat érkezett. Az első kérdésre igennel válaszolók közül 8-an nem akartak korán tornázni, 6-an pedig szerdán rajzolni. Azok, akik a második és harmadik kérdésre is igennel válaszoltak 12-en voltak, de ennek a társaságnak a fele nem szerette volna, ha a tanítás később kezdődik. Hány küldött szavazott minden kérdésre igennel? Hányan szavaztak minden kérdésre nemmel?
*Algebra (Azonosító: AD_20172018_k1k2f4f, AD_20172018_k2k2f4f, AD_20172018_k3k1f4f )
Az osztály matematika órán a faktoriális fogalmát tanulta: egy n pozitív egész szám faktoriálisa az n-nél nem nagyobb pozitív egészek szorzatát jelenti, jelölése n!. Kiszámolták 1-től 20-ig a pozitív egész számok szorzatát, majd a kapott 19-jegyű számot felírták a táblára. Szünetben azonban valaki letörölt néhány számjegyet, így most a táblán a következő egyenlőség látható:
$ 20!=243290200\square 1766\square \square \square \square \square $
ahol a $\square $-ek helyén álló számjegyek már nem olvashatóak. Határozd meg a hiányzó számjegyeket a szorzat kiszámolása nélkül!
*Algebra (Azonosító: AD_20172018_k1k2f5f, AD_20172018_k2k2f5f, AD_20172018_k3k1f5f )
Az első síknegyedben a ( 0; 0 ) pontból kiindulva sorra vesszük az egész koordinátájú pontokat az ábra szerint. (Tehát például a (2; 1 ) pont a 8-as sorszámot kapja.)
a) Határozd meg a ( 12; 2017) pont sorszámát!
b) Melyik ponthoz rendeljük a 2018-as sorszámot?