Legyen $ n $ 3-mal osztható pozitív egész szám. Az $ n - 1, n - 2, \ldots , 2, 1 $ számsorozatból elhagyjuk a 3-mal osztható számokat, majd az első két számot pozitív előjellel, a következő kettőt negatív előjellel, az azután következő kettőt megint pozitív előjellel látjuk el. A kettesével változó előjelezést addig folytatjuk, amíg a számsorozat végére érünk. Bizonyítsuk be, hogy az így kapott számok összege mindig $ n $-nel lesz egyenlő!
Határozzuk meg az $ f(x)=\dfrac{\left( x^2+2021 \right)^2}{x^2}+2022 $ függvény minimumértékét és helyét.
Anna és Balázs a 10 × 10-es szorzótáblán a következő „játékot” játsszák:
- Anna kiválaszt egy függőleges sávot (néhány szomszédos oszlopot) a táblázatban, és a benne szereplő számokat megszorozza (-1)-gyel, majd
- Balázs kiválaszt egy vízszintes sávot (néhány szomszédos sort) a táblázatban, és a benne szereplő számokat megszorozza (-1)-gyel. (Így bizonyos számok akár kétszer is szorzódnak (-1)-gyel.)
Ha például Anna az első három oszlopot, míg Balázs a negyedik sortól a hetedik sorig "választ", akkor a módosított táblázat számai:
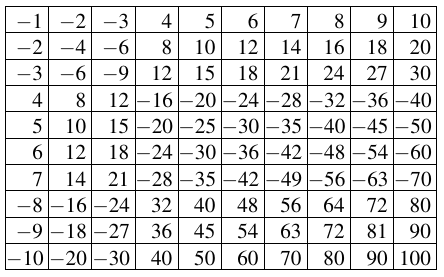
(Anna és Balázs is csak egyszer választanak sávot a "játék" során.)
a) Lehetséges-e, hogy a kapott táblázat 100 darab számát összeadva az összeg 0?
b) Lehetséges-e, hogy a kapott táblázat 100 darab számát összeadva az összeg 1?
Amennyiben a megoldás lehetséges, írjuk le a játék lépéseit is!
Legyen $ O $ az $ ABCD $ négyzet $ CD $ oldalának $ D $-hez közelebbi olyan belső pontja, amelyre teljesül, hogy az $ O $ középpontú $ OD $ sugarú kör, valamint a $ B $ középpontú $ 2\cdot OD $ sugarú kör érinti egymást. Az érintési pontban a két körhöz közös érintőt húzunk. Határozzuk meg az érintő négyzetbe eső szakaszának a négyzet oldalához viszonyított arányát!


