Adott az $ f $ és a $ g $ függvény.
$f:D_f=\mathbb{R}\setminus\left\{ k\cdot \dfrac{\pi} 2;\ k\in\mathbb{Z}\right\}\qquad \to (tg x+ctg x)\cdot \sin x $
a) Igazolja, hogy az így definiált $ f $ függvény konstans!
$ g:D_g=[-7;7]\qquad x\to x^2-6|x|$
b) Számítsa ki a $ g $ függvény zérushelyeit!
c) Adja meg a $ g $ függvény értékkészletét!
Kilenc számkártya fekszik az asztalon.

a) Rakja négy csoportba a kilenc számkártyát úgy, hogy egyikben se legyen együtt egy szám és egy nála kisebb osztója! Adjon meg két lehetséges csoportosítást!
b) Berci körbe rakta a kilenc számkártyát egy nagy papírra, és ha két szám között legalább kettő volt a különbség, akkor a két kártyát összekötötte egy vonallal. Összesen hány vonalat rajzolt meg ily módon Berci?
Csaba az első hat kártya felhasználásával (1, 2, 3, 4, 5, 6) két háromjegyű számot készített. Hívjunk egy ilyen számpárt duónak. (Például egy lehetséges duó: "415 ; 362".) A hat számból több ilyen duót lehet készíteni. Két duót egyenlőnek tekintünk, ha ugyanaz a két különböző háromjegyű szám alkotja. Például a "415 ; 362" és a "362 ; 415" duó egyenlők, de a "362 ; 145" már egy másik duó.
c) Hány különböző duót lehet a hat számkártyából elkészíteni?
Egy mértani sorozat első három tagjának összege 91. A hatodik, a hetedik és a nyolcadik tag összege 2912. Hány tizenhárom-jegyű tagja van a sorozatnak?
Egy könyvkiadó minden negyedévben összesíti, hogy három üzletében melyik szépirodalmi kiadványából fogyott a legtöbb. A legutóbbi összesítéskor mindhárom üzletben ugyanaz a három szerző volt a legnépszerűbb: Arany János, Márai Sándor és József Attila. Az alábbi kördiagramok szemléltetik, hogy az üzletekben milyen arányban adták el ezeknek a szerzőknek a műveit. A kördiagramok az első üzletből 408, a másodikból 432, a harmadikból 216 eladott könyv eloszlásait szemléltetik.
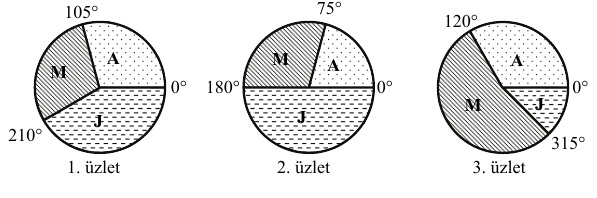
a) A kördiagramok adatai alapján töltse ki az alábbi táblázatot! Melyik szerző műveiből adták el a vizsgált időszakban a legtöbb könyvet?

b) Készítsen olyan oszlopdiagramot a táblázat alapján, amely a vizsgált időszakban a szerzők szerinti összesített forgalmat szemlélteti!
A könyvkiadó a három üzletében minden eladott könyvhöz ad egy sorsjegyet. Ezek a sorsjegyek egy közös sorsoláson vesznek részt negyedévenként. A vizsgált időszakban azok a sorsjegyek vesznek részt a sorsoláson, amelyeket a fenti három szerző műveinek vásárlói kaptak. Két darab 50 ezer forintos könyvutalványt sorsolnak ki köztük.
c) Mennyi annak a valószínűsége, hogy a vizsgált időszak sorsolásán mind a két nyertes sorsjegyet Márai Sándor egy-egy könyvéhez adták, és mindkét könyvet a 2. üzletben vásárolták? Válaszát három tizedesjegy pontossággal adja meg!


