Egy áruházban egy mosóport négyféle kiszerelésben árusítanak. Az első kiszerelés $ 50\% $-kal drágább a harmadiknál, és $ 20\% $-kal kevesebb mosópor van benne, mint a másodikban. A második $ 50\% $-kal több mosóport tartalmaz, mint a harmadik, és $ 25\% $-kal többe kerül, mint az első.

a) Az első három kiszerelés közül melyikben a legalacsonyabb a mosópor egységára?

A negyedik fajta kiszerelést úgy állították össze, hogy annak dobozán a feltüntetett egységár megegyezett az első három kiszerelés átlagos egységárával.

b) Ha a legolcsóbb kiszerelésű dobozon 600 Ft egységárat tüntettek fel, akkor hány forint egységár szerepel a negyedik fajta dobozon?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Legyen $ f(x)=-\dfrac{4x^3} a+\dfrac{3x^2} a+\dfrac{2x} a-a$, ahol $ a $ pozitív valós szám és $ x \in \mathbb{R} $.

a) Igazolja, hogy $ \int\limits_{0}^{a} f(x)\ dx= = - a^3 + a $.

b) Mely pozitív valós $ a $ számokra teljesül, hogy $ \int\limits_{0}^{a} f(x)\ dx\ge0$

c) Az $ x $ mely pozitív valós értéke esetén lesz a $ g(x) = -x^3 + x $ függvénynek lokális (helyi) maximuma?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az $ ABCD $ konvex négyszög oldalegyeneseinek egyenlete rendre:

$ DA: 3x - 4y - 20 = 0 $ , $ AB: 3x + 5y - 20 = 0 $ , $ BC: 4x - 3y +12 = 0 $, $ CD: 5x + 3y +15 = 0 $ .

a) Igazolja, hogy a négyszög átlói az $ x $ és az $ y $ tengelyre illeszkednek, továbbá hogy ennek a négyszögnek nincsen derékszöge!

b) Bizonyítsa be, hogy ez a négyszög húrnégyszög!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Peti levelet írt négy barátjának, Andrásnak, Bélának, Csabának és Daninak, és mindenkinek 1-1 fényképet is akart küldeni a nyaralásról. A négy fénykép különböző volt, és Peti mindegyikük hátlapjára ráírta, kinek szánja. A fényképeket végül figyelmetlenül rakta borítékba, bár mindenki kapott a levelében egy fényképet is.

a1) Hányféleképpen fordulhat elő, hogy csak Andris kapja azt a fényképet, amelyen a saját neve szerepel?

a2) Melyik esemény bekövetkezésének nagyobb a valószínűsége:

- senki sem kapja azt a fényképet, amelyet Peti neki szánt;

vagy

- pontosan egyikük kap olyan fényképet, amelyen a saját neve szerepel?

b) Egy szabályos érme egyik oldalán a 6-os, a másikon pedig a 4-es számjegy látható. Az érmét négyszer egymás után feldobjuk, és a dobott számokat összeadjuk. Milyen értékeket kaphatunk összeg gyanánt? Az egyes összegek dobásának mekkora a valószínűsége?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy $ 90\ m^2 $ területű, trapéz alakú virágágyás párhuzamos oldalainak aránya $ AB : DC = 3: 2 $ . Az ágyást tavasszal és ősszel is az évszaknak megfelelő virágokkal ültetik be. Mindkét alkalommal mindegyik fajta virágból átlagosan 50 virágtövet ültetnek négyzetméterenként. Tavasszal az átlókkal kijelölt négy háromszögre bontották a virágágyást. Az $ ABM $ háromszögbe sárga virágokat, a $ DMC $ háromszögbe fehéret, a maradék két részbe piros virágokat ültettek.

a) A tavaszi parkosításkor hány darab fehér, hány piros és hány sárga virágot ültettek be?

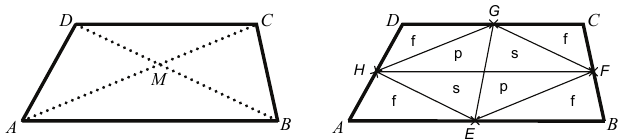
Ősszel a másik ábra alapján tervezték meg a virágok elhelyezését. (Az E, F, G és H pontok a trapéz oldalainak felezőpontjai.) Ekkor is fehér (f), piros (p) és sárga (s) virágokat ültettek a tervrajz alapján.

b) Az őszi parkosításkor hány darab fehér, hány piros és hány sárga virágot ültettek? Válaszait az alábbi táblázatban tüntesse fel!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba