Látogatók
Összes:
9 199 036
Mai:
5 365
216.73.216.41
(IP: 216.73.216.41)
|
1. találat: Matematika emelt szintű érettségi, 2012. május, II. rész, 5. feladat
Témakör: *Geometria (Azonosító: mme_201205_2r05f )
Két egyenes hasábot építünk: $ H_{1} $-et és $ H_{2} $-t. Az építéshez használt négyzetes oszlopok (négyzet alapú egyenes hasábok) egybevágók, magasságuk kétszer akkora, mint az alapélük. A $ H_{1} $ hasáb építésekor a szomszédos négyzetes oszlopokat az oldallapjukkal illesztjük össze, a $ H_{2} $ hasáb építésekor pedig a négyzet alakú alaplapjukkal – az ábra szerint. 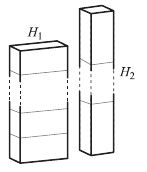
a) A $ H_{1} $ és $ H_{2} $ egyenes hasábok felszínének hányadosa: $\dfrac{A_{H_1}}{A_{H_2} }=0,8 $. Hány négyzetes oszlopot használtunk az egyes hasábok építéséhez, ha $ H_{1} $ -et és $ H_{2} $ -t ugyanannyi négyzetes oszlopból építettük fel? b) Igazolja, hogy a $\left\{ \dfrac{3n+2}{4n+1 }\right\}\ (n\in\mathbb{N}^+) $ sorozat szigorúan monoton csökkenő és korlátos!
*Kombinatorika (Azonosító: mme_201205_2r06f )
Egy középiskolai évfolyam kézilabda házibajnokságán az A, B, C, D, E és F osztály egy-egy csapattal vett részt. a) Hányféle sorrendben végezhettek az osztályok a bajnokságon, ha tudjuk, hogy holtverseny nem volt, és valamilyen sorrendben az A és a B osztály végzett az első két helyen, a D osztály pedig nem lett utolsó? b) Hányféle sorrendben végezhettek az osztályok a bajnokságon, ha tudjuk, hogy holtverseny nem volt, és az E osztály megelőzte az F osztályt? A bajnokságon mindenki mindenkivel egyszer játszott, a győzelemért 2, a döntetlenért 1, a vereségért 0 pont járt. Végül az osztályok sorrendje A, B, C, D, E, F lett, az elért pontszámaik pedig rendre 8, 7, 6, 5, 4 és 0. Tudjuk, hogy a mérkőzéseknek éppen a harmada végződött döntetlenre, és a második helyezett B osztály legyőzte a bajnok A osztályt. c) Mutassa meg, hogy a B és a D osztály közötti mérkőzés döntetlenre végződött!
*Algebra (Azonosító: mme_201205_2r07f )
Az $ y = ax + b $ egyenletű egyenes illeszkedik a $ (2; 6) $ pontra. Tudjuk, hogy $ a < 0 $. Jelölje az $ x $ tengely és az egyenes metszéspontját $ P $, az $ $y tengely és az egyenes metszéspontját pedig $ Q $. Írja fel annak az egyenesnek az egyenletét, amelyre az $ OPQ $ háromszög területe a legkisebb, és számítsa ki ezt a területet ($ O $ a koordináta-rendszer origóját jelöli)!
*Algebra (Azonosító: mme_201205_2r08f )
Egy rendezvényre készülődve 50 poharat tesznek ki egy asztalra. A poharak között 5 olyan van, amelyik hibás, mert csorba a széle. a) Az egyik felszolgáló az asztalról elvesz 10 poharat, és ezekbe üdítőitalt tölt. Számítsa ki annak a valószínűségét, hogy legfeljebb 1 csorba szélű lesz a 10 pohár között! A poharakat előállító gyárban két gépsoron készülnek a poharak, amelyek külsőre mind egyformák. Az első gépsoron gyártott poharak $ 10\% $-a selejtes. b) Számítsa ki annak a valószínűségét, hogy az első gépsoron gyártott poharak közül 15-öt véletlenszerűen, visszatevéssel kiválasztva közöttük pontosan 2 lesz selejtes! A második gépsoron készült poharak $ 4\% $-a selejtes. Az összes pohár 60%-át az első gépsoron, $ 40\% $-át a második gépsoron gyártják, az elkészült poharakat összekeverik. c) Az elkészült poharak közül véletlenszerűen kiválasztunk egyet és azt tapasztaljuk, hogy az selejtes. Mekkora annak a valószínűsége, hogy ez a pohár az első gépsoron készült?
*Geometria (Azonosító: mme_201205_2r09f )
a) Egy derékszögű háromszög oldalhosszai egy számtani sorozat egymást követő tagjai, a legrövidebb oldala 4 egység hosszú. Számítsa ki a háromszög másik két oldalának hosszát! b) Egy háromszög oldalhosszai egy számtani sorozat egymást követő tagjai, a legrövidebb oldala 4 egység hosszú. Tudjuk, hogy a háromszög nem szabályos. Igazolja, hogy a háromszögnek nincs $ 60^\circ $-os szöge!
|
|


