Egy új típusú sorsjegyből 5 millió darab készült, egy sorsjegy ára 200 Ft. Minden egyes sorsjegyen vagy a "Nyert" vagy a "Nem nyert" felirat található, és a nyertes sorsjegyen feltüntetik a nyertes szelvény tulajdonosa által felvehető összeget is. A gyártás során a mellékelt táblázat szerinti eloszlásban készült el az 5 millió sorsjegy.

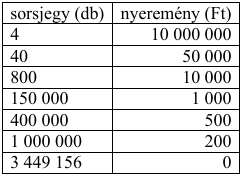
a) Ha minden sorsjegyet eladnának és a nyertesek minden nyereményt felvennének, akkor mekkora lenne a sorsjegyek eladásából származó bevétel és a kifizetett nyeremény különbözete?

b) Aki a kibocsátás után az első sorsjegyet megveszi, mekkora valószínűséggel nyer a sorsjegy áránál többet?

c) Számítsa ki, hogy ebben a szerencsejátékban az első sorsjegyet megvásárló személy nyereségének mennyi a várható értéke! (A nyereség várható értékének kiszámításához nemcsak a megnyerhető összeget, hanem a sorsjegy árát is figye- lembe kell venni.)

Megtekintés helyben: 

   

Megtekintés új oldalon: 

        

Feladatlapba

Két valós szám összege 29. Ha az egyikből elveszünk 15-öt, a másikhoz pedig hozzáadunk 15-öt, az így kapott két szám szorzata éppen ötszöröse lesz az eredeti két szám szorzatának. Melyik lehet ez a két szám?

Megtekintés helyben: 

   

Megtekintés új oldalon: 

        

Feladatlapba

Az alábbi három kifejezés mindegyike esetén adja meg a valós számok halmazának azt a legbővebb részhalmazát, amelyen a kifejezés értelmezhető!

a) $\cos \left(\log_2\sqrt{x }\right) $

b) $\sqrt{\log_2 \left(\cos x\right) } $

c) $\log_{\sqrt{x }}\left(\cos^2 x\right) $

Megtekintés helyben: 

   

Megtekintés új oldalon: 

        

Feladatlapba

A Csendes-óceán egyik kis szigetétől keletre, a szigettől 16 km távolságban elsüllyedt egy föld körüli úton járó vitorlás. A legénység egy mentőcsónakban segítségre vár, a náluk lévő jeladó készülék hatósugara mindössze 6 km. Amikor a vitorlás elsüllyedt, akkor a szigettől délre, a szigettől 24 km távolságra volt egy tengerjáró hajó. Ez a hajó állandóan északkeleti irányba halad, a hajótöröttek pedig a vitorlás elsüllyedésének helyéről folyamatosan küldik a vészjeleket.

a) Igazolja, hogy a tengerjáró legénysége észlelheti a segélykérő jelzést!

Egy 1,5 km magasságban haladó repülőgép éppen a sziget felett van, amikor a repülőgép fedélzeti műszerei észlelik a tengerjáró hajót, amely a vitorlás elsüllyedése óta 20 km-t tett meg.

b) Mekkora depresszió szög (lehajlási szög) alatt észlelik a műszerek a tengerjárót? Válaszát fokban, egészre kerekítve adja meg!

Számításai során a Föld görbületétől tekintsen el!

Megtekintés helyben: 

   

Megtekintés új oldalon: 

        

Feladatlapba