1. találat: Matematika emelt szintű érettségi, 2017. október, II. rész, 5. feladat
Témakör: *Kombinatorika (Azonosító: mme_201710_2r05f )
A laptopokban is használt B típusú lítiumion-akkumulátorok töltéskapacitása minden teljes töltési ciklusnál az előző értékének körülbelül 0,06%-ával csökken.
a) Hány százalékkal csökkent az új akkumulátor töltéskapacitása, ha 350 teljes töltési ciklust végeztek vele?
Egy B típusú akkumulátorral minden évben körülbelül 200 teljes töltési ciklust végeznek. (Tételezzük fel, hogy két töltési ciklus között mindig ugyanannyi idő telik el.)
b) Mennyi a felezési ideje a kezdetben új akkumulátor töltéskapacitásának (azaz töltési kapacitása mennyi idő alatt csökken a felére)?
Egy használt laptop-akkumulátorokat árusító üzletben a 25 azonos típusú akkumulátor töltéskapacitása 60% és 80% között van, de közülük csak 10-nek kisebb a töltéskapacitása 70%-nál. Egy vevő a 25 akkumulátor közül hármat vásárol meg.
c) Ha a három akkumulátort véletlenszerűen választja ki, akkor mennyi a valószínűsége annak, hogy legfeljebb az egyiknek lesz 70%-nál kisebb a töltéskapacitása?
*Algebra (Azonosító: mme_201710_2r06f )
a) Ha $ a|b $ igaz, akkor $ a|b^2 $ is teljesül (a és b pozitív egész számok). Fogalmazza meg a fenti (igaz) állítás megfordítását, és állapítsa meg a megfordítás logikai értékét is! Válaszát indokolja! (a|b azt jelenti, hogy az a egész szám osztója a b egész számnak.)
b) Hány olyan n pozitív egész szám van, amelyhez létezik olyan p (pozitív) prímszám, amelyre az $ n^2- pn $ különbség is egy (pozitív) prímszámmal egyenlő?
Egy lapra 10 pontot rajzoltunk, majd ezeket megszámoztuk 1-től 10-ig. Ezután minden egyes pontot egy-egy vonallal „összekötünk” a lapon szereplő összes olyan ponttal, amelyhez írt szám a kiválasztott ponthoz írt számnak osztója. (Például azt a pontot, amelyhez a 6-ot írtuk, összekötöttük mind a négy ponttal, amelyhez a 6 valamelyik osztóját írtuk.)
c) Igazolja, hogy az így kapott 10 csúcsú gráf nem egyszerű gráf!
d) Igazolja, hogy a gráf éleinek száma páratlan! a
*Kombinatorika (Azonosító: mme_201710_2r07f )
A Téglácska csokiszelet gyártója akciót indít: ha a szerencsés vásárló a csokiszelet csomagolásának belső oldalán a "Nyert" feliratot találja, akkor ezzel egy újabb szelet csokit nyert. A gyártó úgy reklámozza a termékét, hogy "minden ötödik csoki nyer". (Ez úgy tekinthető, hogy minden egyes csoki 0,2 valószínűséggel nyer.)
a) Juli öt szelet csokoládét vásárol. Mennyi annak a valószínűsége, hogy az öt szelet csoki között legalább egy nyerő csoki lesz?
Pali is öt szelet csokoládét vásárolt, és végül hét szelet csokival tért haza a boltból, mert nyert még kettőt.
b) Vizsgálja meg, hogy az alábbi két esemény közül melyiknek nagyobb a valószínűsége!
I. Ha valaki megvásárol öt szelet csokit, akkor azok között két nyerő csoki lesz, de a két nyereménycsoki egyike sem nyer.
II. Ha valaki megvásárol öt szelet csokit, akkor azok között egy nyerő csoki lesz, a nyereménycsoki nyer egy hetedik szelet csokit, de az már nem nyer.
Egy másik akcióban a csokiszelet térfogatát $ 20\% $-kal megnövelték, de továbbra is változatlan áron adták. A csokiszelet téglatest alakú, az eredeti és a megnövelt szelet (matematikai értelemben) hasonló. Az akciós szelet 1 cm-rel hosszabb az eredeti csokiszeletnél.
c) Határozza meg az eredeti csokiszelet hosszúságát! Válaszát egész cm-re kerekítve adja meg! a
*Geometria (Azonosító: mme_201710_2r08f )
Egy egyesületi összejövetel társaságához 5 nő és 4 férfi csatlakozott, így a nők aránya a korábbi $ 25\% $-ról $ 36\% $-ra nőtt.
a) Hány főből állt az eredeti társaság?
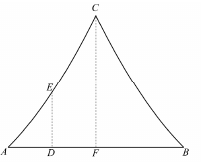
Az ábrán az egyesület székházának függőleges síkú homlokzata látható, amelyet az AC és BC egybevágó parabolaívek határolnak. A parabolák tengelye egy-egy függőleges egyenes, ezek az AB szakasz felezőmerőlegesére szimmetrikusan helyezkednek el. A homlokzat szélessége $ AB = 8 $ méter, magassága $ FC = 6 $ méter, az AF szakasz D felezőpontjában mért tetőmagasság pedig $ DE = 2,5 $ méter.
b) Hány négyzetméter a homlokzat területe?
*Algebra (Azonosító: mme_201710_2r09f )
A pozitív páratlan számokat "háromszög" alakban rendezzük el a következők szerint: az első oszlopba írjuk az első páratlan számot, a második oszlopba a következő kettőt, a harmadik oszlopba a következő hármat, és így tovább. Például az ötödik oszlop negyedik helyén a 27 áll (lásd az ábrát is).

a) Hányadik oszlop hányadik helyén áll a 99?
b) Határozza meg a 2017. oszlopban álló első számot!
c) Igazolja, hogy az $ n $-edik oszlopban álló számok összege $ n^3\ (n\in\mathbb{Z}^+) $.


