Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
LátogatókÖsszes: 6 019 564 Mai: 2 417 HonlapokSULINET Matematika Oktatási Hivatal Versenyvizsga portál Matematika Portálok |
1. találat: Matematika középszintű érettségi, 2014. május, I. rész, 1. feladat Témakör: *Halmazok ( metszet, különbség) (Azonosító: mmk_201405_1r01f ) Legyen A halmaz a 8-nál nem nagyobb pozitív egész számok halmaza, B pedig a 3-mal osztható egyjegyű pozitív egész számok halmaza. Elemeinek felsorolásával adja meg az A, a B, az $A \cap B$ és az $A \setminus B$ halmazt! Témakör: *Algebra ( százalék) (Azonosító: mmk_201405_1r02f ) Egy konzerv tömege a konzervdobozzal együtt 750 gramm. A konzervdoboz tömege a teljes tömeg $ 12\%$-a. Hány gramm a konzerv tartalma? Témakör: *Algebra ( másodfokú) (Azonosító: mmk_201405_1r03f ) Oldja meg a következő egyenletet a valós számok halmazán:$(x-3)^2+2x=14$. Válaszát indokolja! Témakör: *Függvények ( másodfokú, lineáris) (Azonosító: mmk_201405_1r04f ) Válassza ki az f függvény hozzárendelési szabályát az A, B, C, D lehetőségek közül úgy, hogy az megfeleljen az alábbi értéktáblázatnak:
$\textbf{A:} f(x)=2x \qquad \textbf{B:} f(x)=x^2 \qquad \textbf{C:} f(x)=-2x \qquad \textbf{D:} f(x)=-x^2 $ Témakör: *Halmazok (Azonosító: mmk_201405_1r05f ) Egy osztályban 25-en tanulnak angolul, 17-en tanulnak németül. E két nyelv közül legalább az egyiket mindenki tanulja. Hányan tanulják mindkét nyelvet, ha az osztály létszáma 30? Témakör: *Algebra ( százalék) (Azonosító: mmk_201405_1r06f ) Egy termék árát az egyik hónapban $ 20\%$-kal, majd a következő hónapban újabb $ 20\%$-kal megemelték. A két áremelés együttesen hány százalékos áremelésnek felel meg? Válaszát indokolja! Témakör: *Számelmélet ( oszthatóság) (Azonosító: mmk_201405_1r07f ) Melyik számjegy állhat a $\overline{2582X}$ ötjegyű számban az X helyén, ha a szám osztható 3-mal? Válaszát indokolja! Témakör: *Függvények ( abszolútérték) (Azonosító: mmk_201405_1r08f ) Az ábrán a [–1; 5] intervallumon értelmezett függvény grafikonja látható. Válassza ki a felsoroltakból a függvény hozzárendelési szabályát!
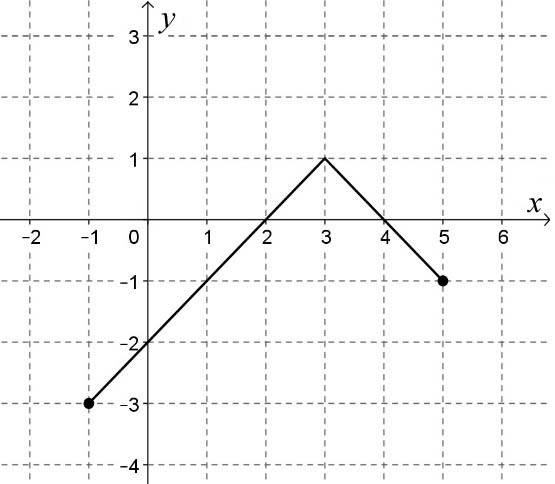
$\textbf{A}: x \mapsto \left | x-3 \right |+1 \quad \textbf{B}: x \mapsto -\left | x+3 \right |+1 \\ \textbf{C}: x \mapsto -\left | x-3 \right |+1 \quad \textbf{D}: x \mapsto -\left | x+3 \right |-1$ Témakör: *Algebra ( logaritmus) (Azonosító: mmk_201405_1r09f ) Adja meg az x értékét, ha $\log_2(x+1)=5$ . Témakör: *Kombinatorika ( gráfok) (Azonosító: mmk_201405_1r10f ) Egy irodai számítógép-hálózat hat gépből áll. Mindegyik gép ezek közül három másikkal van közvetlenül összekötve. Rajzoljon egy olyan gráfot, amely ezt a hálózatot szemlélteti! Témakör: *Geometria ( Thalesz-tétel, Pitagorasz-tétel) (Azonosító: mmk_201405_1r11f ) Egy téglalap szomszédos oldalainak hossza 4,2 cm és 5,6 cm. Mekkora a téglalap körülírt körének sugara? Válaszát indokolja! Témakör: *Valószínűségszámítás (Azonosító: mmk_201405_1r12f ) Egy kalapban 3 piros, 4 kék és 5 zöld golyó van. Találomra kihúzunk a kalapból egy golyót. Adja meg annak valószínűségét, hogy a kihúzott golyó nem piros!
|
KeresésHonlapokKözépiskolai Matematikai és Fizikai Lapok Wolfram Alpha Art of Problem Solving Kvant IMO |
|||||||||||||||||
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
| |||||||||||||||||||
| |||||||||||||||||||
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
|
|
1082 Budapest, Horváth Mihály tér 8. OM azonosító: 035277 |
Joomla template: szsnjm4-001 (c) Szoldatics József 2011/2024
www.szolda.hu
www.szolda.hu