Feladatbank keresés

Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium

Látogatók

Összes:

10 719 514

Mai:

1 939

18-97-14-88.crawl.commoncrawl.org
(IP: 18.97.14.88)

Honlapok

SULINET Matematika

Oktatási Hivatal

Versenyvizsga portál

Matematika Portálok

Berzsenyi Dániel Gimnázium

Óbudai Árpád Gimnázium

Szent István Gimnázium

Békásmegyeri Veres Péter Gimnázium

Első lap
1
Utolso lap

Találatok száma: 12 (listázott találatok: 1 ... 12)

1. találat: Matematika középszintű érettségi, 2019. május I. rész, 1. feladat
Témakör: *Algebra (Azonosító: mmk_201905_1r01f )

Oldja meg az alábbi egyenletet a valós számok halmazán! $ x^2 - 2x - 8 = 0 $

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

2. találat: Matematika középszintű érettségi, 2019. május I. rész, 2. feladat
Témakör: *Geometria (Azonosító: mmk_201905_1r02f )

Egy háromszög belső szögeinek aránya 2 : 3 : 7. Hány fokos a háromszög legkisebb szöge?

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

3. találat: Matematika középszintű érettségi, 2019. május I. rész, 3. feladat
Témakör: *Algebra (Azonosító: mmk_201905_1r03f )

Egy üdítőital címkéjén az olvasható, hogy egy pohár (250 ml) üdítő elfogyasztásával 12 g cukrot viszünk a szervezetünkbe, és ez a mennyiség az ajánlott napi maximális cukorbevitel $ 30\% $-a. Hány gramm az ajánlott napi maximális cukorbevitel?

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

4. találat: Matematika középszintű érettségi, 2019. május I. rész, 4. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201905_1r04f )

Adottak a következő halmazok: $ A = \left\{ 2; 3; 5; 7; 11; 13; 17; 19 \right\} $ ; $ B = \left\{ 1; 4; 7; 10; 13; 16; 19 \right\};$ $ C = \left\{ 1; 2; 3; 5; 8 \right\}; 13 $. Elemei felsorolásával adja meg a $ C / A $ és az $ ( A \cup B ) \cap C $ halmazt!

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

5. találat: Matematika középszintű érettségi, 2019. május I. rész, 5. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201905_1r05f )

Egy ötpontú gráfnak 7 éle van. Mennyi a gráfban a csúcsok fokszámának összege?

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

6. találat: Matematika középszintű érettségi, 2019. május I. rész, 6. feladat
Témakör: *Kombinatorika (Azonosító: mmk_201905_1r06f )

Négy gombóc fagylaltot vásárolunk tölcsérbe: egy csokoládét, egy vaníliát, egy puncsot és egy eperízűt. Hányféle olyan sorrendje lehetséges ennek a négy gombócnak, amelynél nem a csokoládé a legalsó?

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

7. találat: Matematika középszintű érettségi, 2019. május I. rész, 7. feladat
Témakör: *Geometria (Azonosító: mmk_201905_1r07f )

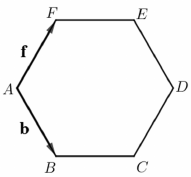
Az $ ABCDEF $ szabályos hatszögben $ \vec{b} = \overrightarrow{AB} $ és $ \vec{f} = \overrightarrow{AF }$ . Fejezze ki a $ \vec{b} $ és $ \vec{f} $ vektorok segítségével az $ \overrightarrow{AD} $ vektort!

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

8. találat: Matematika középszintű érettségi, 2019. május I. rész, 8. feladat
Témakör: *Geometria (Azonosító: mmk_201905_1r08f )

Az alábbi hat szám közül válassza ki az összes olyan számot, amely osztható 3-mal, de nem osztható 5-tel!

$ 895, 1222, 1458, 1526, 1848, 1990 $

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

9. találat: Matematika középszintű érettségi, 2019. május I. rész, 9. feladat
Témakör: *Geometria (Azonosító: mmk_201905_1r09f )

Egy középület akadálymentesítésekor a bejárathoz egyenletesen emelkedő rámpát építenek, hogy kerekesszékkel és babakocsival is be lehessen jutni az épületbe. A rámpa hossza 3 méter, és a járda szintjétől 60 centiméter magasra visz. Hány fokos a rámpa emelkedési szöge? Megoldását részletezze!

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

10. találat: Matematika középszintű érettségi, 2019. május I. rész, 10. feladat 10
Témakör: *Algebra (Azonosító: mmk_201905_1r10f )

Az $ f $ egyenes egyenlete $ 2x – y = 5 $.

a) Adja meg az $ f $ egy normálvektorát!

b) Írja fel annak az egyenesnek az egyenletét, amely párhuzamos az $ f $ egyenessel, és átmegy a $ (2; 1) $ ponton!

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

11. találat: Matematika középszintű érettségi, 2019. május I. rész, 11. feladat
Témakör: *Algebra (Azonosító: mmk_201905_1r11f )

Egy mértani sorozat második tagja $ 6 $, harmadik tagja $ -12 $. Számítsa ki a sorozat első tíz tagjának összegét! Megoldását részletezze!