1. találat: Matematika középszintű érettségi, 2019. május II. rész, 13. feladat
Témakör: *Algebra (Azonosító: mmk_201905_2r13f )
a) Hány olyan háromjegyű egész szám van, amelyre igaz az alábbi egyenlőtlenség?
$ \dfrac{x}{ 3}+ \dfrac{x}{ 6}\ge \dfrac{x}{4}+230 $
b) Oldja meg az alábbi egyenletet a valós számok halmazán!
$ 3 \cdot 4^x + 4^{x +1} = 896 $
*Algebra (Azonosító: mmk_201905_2r14f )
Adott az $ f: R \rightarrow R, f (x) = x^2 + 4x + 3 $ függvény.
a) Írja fel két elsőfokú tényező szorzataként az $ x^2 + 4x + 3 $ kifejezést!
b) A $ P(–6,5; y) $ pont illeszkedik az $ f $ grafikonjára. Számítsa ki $ y $ értékét!
c) Az alábbi grafikonok közül válassza ki az $ f $ függvény grafikonját (karikázza be a megfelelő betűt), és határozza meg az $ f $ értékkészletét!
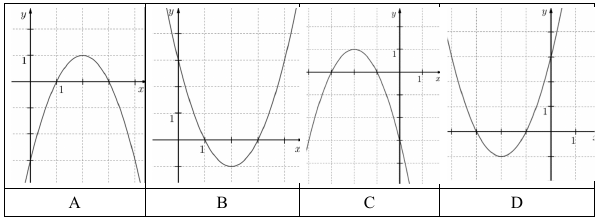
Adott a $ g: R \rightarrow R, g (x) = x^2 - 6 x + 5 $ függvény. Az a három pont, ahol a $ g $ grafikonja
metszi a koordinátatengelyeket, egy háromszöget határoz meg.
d) Határozza meg ennek a háromszögnek a területét!
*Geometria (Azonosító: mmk_201905_2r15f )
Az $ ABCD $ négyzet oldalának hossza $ 12 $ egység. A négyzet belsejében kijelöltük az $ E $ pontot úgy, hogy $ BE = CE = 12 $ egység legyen.
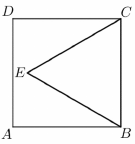
a) Számítsa ki az $ A $ és $ E $ pontok távolságát!
Egy bronzból készült, szabályos négyoldalú gúla alakú tömör test (piramis) minden éle $ 10\ cm $ hosszúságú.
b) Számítsa ki a gúla tömegét, ha $ 1\ dm^3 $ bronz tömege $ 8\ kg $!
*Algebra (Azonosító: mmk_201905_2r16f )
Péter elhatározza, hogy összegyűjt 3,5 millió Ft-ot egy használt elektromos autó vásárlására, mégpedig úgy, hogy havonta egyre több pénzt tesz félre a takarékszámláján. Az első hónapban 50 000 Ft-ot tesz félre, majd minden hónapban 1000 Ft-tal többet, mint az azt megelőző hónapban. (A számlán gyűjtött összeg kamatozásával Péter nem számol.)
a) Össze tud-e így gyűjteni Péter 4 év alatt 3,5 millió forintot?
A világon gyártott elektromos autók számának 2012 és 2017 közötti alakulását az alábbi táblázat mutatja.

b) Szemléltesse a táblázat adatait oszlopdiagramon!
Péter az előző táblázat adatai alapján olyan matematikai modellt alkotott, amely az elekt- romos autók számát exponenciálisan növekedőnek tekinti. E szerint, ha a 2012 óta eltelt évek száma $ x $, akkor az elektromos autók számát (millió darabra) megközelítőleg az $ f ( x) = 0,122 \cdot 2^{0,822 x} $ összefüggés adja meg.
c) A modell alapján számolva melyik évben érheti el az elektromos autók száma a 25 millió darabot?
Egy elektromos autókat gyártó cég öt különböző típusú autót gyárt. A készülő reklámfüzet fedőlapjára az ötféle típus közül egy vagy több (akár mind az öt) autótípus képét szeretné elhelyezni a grafikus.
d)Hány lehetőség közül választhat a tervezés során? (Két lehetőség különböző, ha az egyikben szerepel olyan autótípus, amely a másikban nem.)
*Algebra (Azonosító: mmk_201905_2r17f )
A Föld teljes vízkészlete (jég, víz és vízgőz) folyékony halmazállapotban közel 1400 millió $ km^3 $lenne. Ennek a vízkészletnek csupán $ 3\% $-a édesvíz, melynek valójában mindössze $ 20\% $-a folyékony halmazállapotú (a többi főleg a sarkvidék jégtakarójában található fagyott, szilárd állapotban). a
) Számítsa ki, hogy hány kilométer lenne annak a legkisebb gömbnek a sugara, amelybe összegyűjthetnénk a Föld folyékony édesvízkészletét! Válaszát egész kilométerre kerekítve adja meg!
Az ábrán egy környezetvédő szervezet logójának ki nem színezett terve látható.
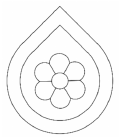
A logó kilenc tartományát három színnel (sárga, kék és zöld) szeretnénk kiszínezni úgy, hogy a szomszédos tartományok kü- lönböző színűek legyenek. (Két tartomány szomszédos, ha a határvo- nalaiknak van közös pontja. Egy-egy tartomány színezéséhez egy színt használhatunk.)
b) Hányféleképpen lehet a logót a feltételeknek megfelelően kiszínezni?
Egy iskolai italautomata meghibásodott, és véletlenszerűen ad szénsavas, illetve szénsav- mentes vizet. A diákok tapasztalata szerint, ha valaki szénsavmentes vizet kér, akkor csak 0,8 a valószínűsége annak, hogy valóban szénsavmentes vizet kap. Anna a hét mind az öt munkanapján egy-egy szénsavmentes vizet szeretne vásárolni az automatából, így minden nap az ennek megfelelő gombot nyomja meg.
c)Mennyi a valószínűsége annak, hogy legalább négy napon valóban szénsavmentes vizet ad az automata?
*Algebra (Azonosító: mmk_201905_2r18f )
Az ábrán egy kis múzeum alaprajzát látjuk.
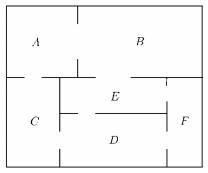
A múzeum termei közötti kapcsolatot gráffal is szemléltethetjük. A gráf pontjai a termek, élei pedig az átjárók a termek kö- zött. (Egy él egy átjárót szemléltet két terem között.)
a) Rajzolja fel a múzeum termeit és átjáróit szemléltető gráfot!
A múzeumba háromféle belépőjegyet lehet váltani:

Januárban négyszer annyi kedvezményes belépőjegyet adtak el, mint teljes árú jegyet, továbbá az eladott fotójegyek száma az eladott teljes árú jegyek számának $ 12,5\% $-a volt. A múzeum belépőjegy-eladásból származó bevétele januárban 912 600 Ft volt.
b) Hány belépőjegyet adtak el januárban összesen?
Csilla, Dezső, Emese, Feri és Gyöngyi délelőtt 10-re beszéltek meg találkozót a múzeum előtt. Sorban egymás után érkeznek (különböző időpontokban), véletlenszerűen.
c) Mennyi a valószínűsége annak, hogy legfeljebb egy lánynak kell várakoznia fiúra?
A kiállításon több gondolkodtató, minimalista kép is szerepel. Dezső szerint az ábrán látható, csatlakozó félköröket ábrázoló kép címe azért "Egyenlőség", mert a felső és az alsó görbe vonal hossza egyenlő.
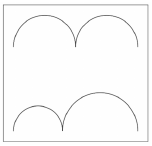
A felső görbét alkotó két egyforma félkör átmérőjének összege 48 cm. Az alsó görbét alkotó két félkör átmérőjének összege szintén 48 cm.
d) Igaz-e Dezső sejtése, hogy a két görbe vonal hossza egyenlő?


