1. találat: Matematika középszintű érettségi, 2020. május I. rész, 1. feladat
Témakör: *Geometria (Azonosító: mmk_202005_1r01f )
Egy téglatest egy csúcsból kiinduló három élének hossza: 3 dm, 2 dm és 2,5 dm. Hány négyzetdeciméter a test felszíne?
*Kombinatorika (Azonosító: mmk_202005_1r02f )
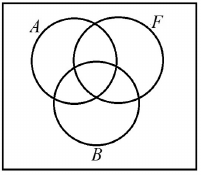
Az alábbi ábra egy érettségiző évfolyam diákjainak a halmazát szemlélteti. $ A $ jelöli az angol nyelvből, $ B $ a biológiából, $ F $ pedig a fizikából érettségiző diákok halmazát. Színezze be az ábrának azt a részét, amely azon diákok halmazát jelöli, akik angol nyelvből és biológiából érettségiznek, de fizikából nem!
*Algebra (Azonosító: mmk_202005_1r03f )
A 2 hányadik hatványával egyenlő az alábbi kifejezés?
$ \dfrac{2^7\cdot \left(2^3 \right)^4}{2^5} $
*Kombinatorika (Azonosító: mmk_202005_1r04f )
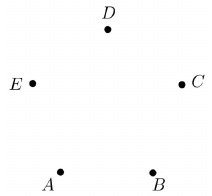
Egy nemzetközi konferencia 5 résztvevője áll egy asztal körül a kávészünetben (jelölje őket A, B, C, D, illetve E). Tudjuk, hogy A ismer mindenkit az asztalnál. B nem ismeri E-t, de a többieket ismeri. C két résztvevőt ismer, D pedig hármat. Ábrázolja az ötfős társaság tagjai közötti ismeretségeket egy gráffal, és adja meg, hogy kiket ismer az asztalnál az E-vel jelölt személy! (Minden ismeretség kölcsönös.)
*Algebra (Azonosító: mmk_202005_1r05f )
Adja meg az alábbi állítások logikai értékét (igaz vagy hamis)!
A: Ha egy pozitív egész szám osztója 24-nek, akkor osztója 12-nek is.
B: Ha egy pozitív egész szám osztható 12-vel, akkor osztható 6-tal is.
C: Ha egy pozitív egész szám osztható 2-vel és 4-gyel, akkor osztható 8-cal is.
*Algebra (Azonosító: mmk_202005_1r06f )
Ábrázolja a $ [−1; 2] $ intervallumon értelmezett $ x \rightarrow ( x - 1)^2 $ függvényt!
*Kombinatorika (Azonosító: mmk_202005_1r07f )
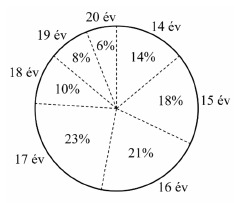
Egy több száz fős gimnázium diákjai életkorának eloszlását mutatja az alábbi kördiagram. Állapítsa meg a diákok életkorának terjedelmét, móduszát és mediánját!
*Algebra (Azonosító: mmk_202005_1r08f )
Hány olyan egész szám van, amelynek az abszolút értéke kisebb 6-nál?
*Algebra (Azonosító: mmk_202005_1r09f )
Tudjuk, hogy az $ \dfrac 5 7 = 0,714285 $ végtelen szakaszos tizedes tört. Adja meg a tizedesvessző utáni századik számjegyet! Válaszát indokolja!
*Geometria (Azonosító: mmk_202005_1r10f )
Egy háromszög 11 cm hosszú oldalával szemközti szöge $ 45^\circ $-os. Ennek a háromszögnek van egy $ 122^\circ $-os szöge is. Hány cm hosszú a háromszög $ 122^\circ $-os szögével szemközti oldala? Válaszát indokolja!
*Algebra (Azonosító: mmk_202005_1r11f )
Egy mértani sorozat első tagja $ \dfrac 1 2 $, második tagja 3. Határozza meg a sorozat harmadik tagját!
*Kombinatorika (Azonosító: mmk_202005_1r12f )
Egy szabályos dobókockával háromszor dobunk, majd a dobott számokat (a dobások sorrendjében) balról jobbra egymás mellé írjuk. Így egy háromjegyű számot kapunk. Mennyi a valószínűsége annak, hogy a kapott háromjegyű szám 500-nál nagyobb lesz? Válaszát indokolja!


