Jelölje $ a_n $ az $ \dfrac{n!}{2^n} $ tört tovább nem egyszerűsíthető alakjában a nevező értékét. Például $ a_5 = 4 $, mert
$ \dfrac{5!}{2^5}=\dfrac{1 \cdot 2\cdot 3 \cdot 4 \cdot 5}{32}=\dfrac{120}{32}=\dfrac{15}{4} $
Tekintsük az $ a_1, a_2, a_3, \ldots, a_{2022} $ számokat.
a) Mennyi ezen $ 2022 $ darab szám minimuma, és ez a minimum hányszor szerepel a $ 2022 $ szám között?
b) Mennyi ezen $ 2022 $ darab szám maximuma, és ez a maximum hányszor szerepel a $ 2022 $ szám között?
Andor rendszeresen kerékpározik. Egy alkalommal, amikor hazaér a biciklizésből, testvére, Bendegúz kérdezi tőle, hogy mekkora távot tekert. Andor így felel: "Te jó vagy matekból, próbáld meg kitalálni. Azt elárulom, hogy összesen 2 óra 24 percet bicikliztem, valamekkora táv után visszafordultam, és ugyanazon az úton jöttem haza, amelyiken odafelé mentem. Lejtőn lefelé $ 45\,\dfrac{km}{h} $, emelkedőn felfelé $ 15\,\dfrac{km}{h} $ sebességgel haladtam."
Bendegúz: „Gondolom, vízszintes része is volt az útnak.”
Andor: „Volt, persze.”
Bendegúz: „Akkor ennyi adatból még nem tudom megmondani, hogy mekkora távot teljesítettél.”
Andor erre ezt mondja: „Ha azt is megmondanám, hogy vízszintes úton mekkora sebességgel haladtam, akkor már egyértelműen tudnál válaszolni, de ezt nem mondom meg.”
Bendegúz némi számolás után így szólt: „Már tudom a választ.” És valóban meg tudta mondani, hogy Andor hány kilométert biciklizett. Mi volt Bendegúz válasza?
Határozzuk meg azokat a nemnegatív egész számokból álló $ (x; y) $ számpárokat, amelyekre
$ (xy - 7)^2 = x^2 + y^2 $
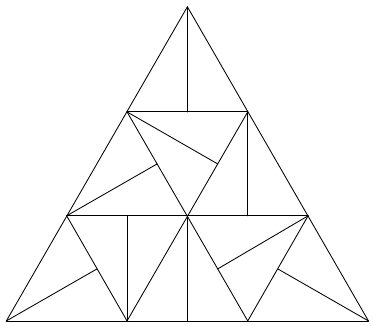
Egy szabályos háromszög minden oldalát n egyenlő részre osztjuk, majd az osztáspontokon át a megfelelő oldalakkal párhuzamosakat húzva felosztjuk a háromszögünket n2 darab kisebb szabályos háromszögre. Ezek után a kisebb háromszögek közül néhánynak megrajzoljuk az egyik súlyvonalát arra figyelve, hogy egyetlen súlyvonalnak se legyen semelyik másik súlyvonallal közös (vég)pontja. Például az alábbi ábrán n = 3 esetén mind a kilenc kisebb háromszög egy-egy súlyvonalát megrajzoltuk. Jelölje $ s(n) $ azt a legnagyobb számot, amennyi súlyvonal szabályosan berajzolható adott n esetén. (A lenti ábra alapján $ s(3) = 9 $ például.)
Az $ ABCDE $ konvex ötszögben $ EAB\sphericalangle = 60^\circ $ , $ ABC\sphericalangle = 100^\circ $ és $ BCD\sphericalangle = 140^\circ $. Bizonyítsuk be, hogy az ötszög lefedhető egy olyan körrel, amelynek sugara $ \dfrac{2}{3}DA $ hosszúságú.


