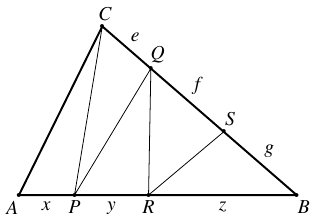
Az $ ABC $ háromszöget az ábra szerint feldaraboljuk öt egyenlő területű háromszögre. A keletkezett öt kis háromszög azon oldalainak hossza, amelyek az $ ABC $ háromszög oldalaira esnek, egész számok. Legalább mekkora az $ ABC $ háromszög kerülete?
Egy matematika szakkörre hatan járnak. Karácsony előtt elhatározzák, hogy megajándékozzák egymást oly módon, hogy mindegyikük nevét felírják egy cédulára, a neveket egy dobozba teszik, majd sorban kihúznak egy-egy nevet. Ha valaki a saját nevét húzza, akkor a sorsolást megismétlik. Végül mind a hatan kihúznak egy nevet, és senki nem a sajátját. Az ajándékozást úgy bonyolítják le, hogy először egyikük odaadja az ajándékát annak, akit húzott, ezután az, aki kapta, szintén odaadja az ajándékát annak, akit húzott, és így tovább. Ekkor két eset lehetséges:
(1) Az ajándékozást kezdő diák lesz a hatodik, aki megkapja a neki szánt ajándékot, ekkor az ajándékozási lánc végigér, mindenki átadta az ajándékát.
(2) Amikor az ajándékozást kezdő diák megkapja az ajándékot, akkor lesz olyan, aki még nem adott és nem is kapott ajándékot. Ezért az ajándékozás folyamatát valaki, aki még nem adott át ajándékot, újra kezdi.
Az (1) vagy a (2) esemény bekövetkezésének nagyobb az esélye?
Mely valós a számok esetén van három különböző valós gyöke az $ x^3 + a(1 - a)x − a^2 = 0 $
egyenletnek?
Legyen $ k \ge 3 $ tetszőleges páratlan szám. Igazoljuk, hogy végtelen sokféleképpen jelölhető ki $ k $ darab egymást követő pozitív egész szám oly módon, hogy ezek köbeinek összege osztható legyen $ 2024 $-gyel.


